Forward
It has been a year since the previous one was published and I knew it the very beginning that it may contain bugs but I was still shocked so many of them.
Now, during the Chinese Spring Festival, the would-be idle time, I refactored the code. Hope the best.
The following are some screenshots from this new release. If you have some experience of the field, I think you will not feel too strange what the pictures want to tell. Anyway, please download and run it.
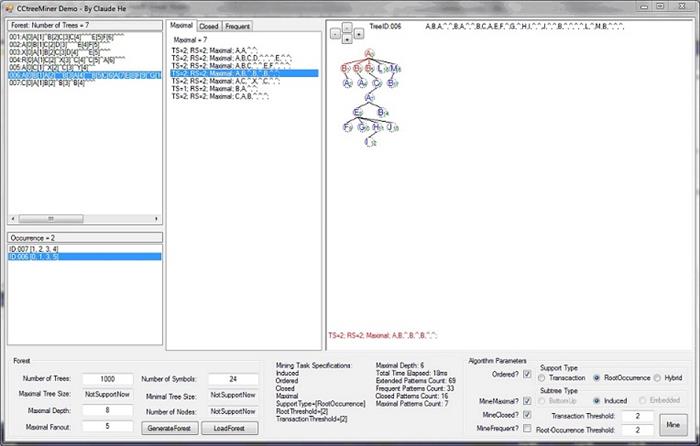

I suggest that you have basic ideas about Subtree Mining. If not, here is a brief description:
Given a limited set of trees, find those subtrees that appears quite often.
For example, in the trees displayed in the above picture, subtree (pattern) A,B,^ appears many times (you can see 5 of them here) in the given trees; Subtree Mining is to find subtrees like this.
However, there are many issues involved.
For this article, it would be better if you know very well about related items like frequent, closed, maximal, induced, embedded, preorder representation, text tree, pattern tree, ordered tree, canonical form and etc. Else you probably want to read my previous article especially the cited references. I also find a excellent book that discussed in detail to this problem namely Mining of Data with Complex Structures by Fedja Hadzic,Henry Tan, and Tharam S.Dillon.
*****************************
Now we get started.
Why We Need Frequent Subtree Mining?
The following is from Wiki.
Domains in which frequent subtree mining is useful tend to involve complex relationships between data entities: for instance, the analysis of XML documents often requires frequent subtree mining. Another domain where this is useful is the web usage mining problem: since the actions taken by users when visiting a web site can be recorded and categorized in many different ways, complex databases of trees need to be analyzed with frequent subtree mining. Other domains in which frequent subtree mining is useful include computational biology, RNA structure analysis, pattern recognition, bioinformatics, and analysis of the KEGG GLYCAN database.
In the following, I will continue my previous article and further explain the ideas behind CCTreeMiner algorithm.
Pattern Generation
How to generate new patterns?
1. Every PatternTree (except 1P or 2P) is created by its parent patterns via connection or combination.
2. 1-patterns and 2-patterns are generated by scanning the input transaction database.
Frequent Determination
Given a support type, how to determine if a pattern is frequent?
First, calculate transaction support and root occurrence support.
For Frequent-1s and Frequent-2s, their root occurrences and transaction occurrences are calculated by means of scanning the input transaction database. And for any pattern larger than 2, the two supports are calculated while joining (connection or combination) its parents.
Secondly, evaluate frequency against support type. If a pattern is frequent, then:
- Transactional support: its number of transaction occurrences (transaction support) should be larger than or equal to transaction threshold.
- Root-Occurrence support: its number root occurrences (root occurrence support) should be larger than or equal to root-occurrence threshold.
- Hybrid support: both of the occurrence numbers should be larger than or equal to the thresholds respectively.
Closed & Maximal Determination
According to its definition, a pattern’s closed property is determined by the given support type and the two kinds of matches involved. See the following (Note occurrence match implies transaction match):
| Support Type
| Has Root Occurrence Match
| Has Transaction Match
| Closed?
|
| Transaction
| Yes
| --
| No
|
|
| No
| Yes
| No
|
|
| --
| No
| Yes
|
| Root Occurrence
| Yes
| --
| No
|
|
| No
| Yes
| Yes
|
|
| --
| No
| Yes
|
| Hybrid
| Yes
| --
| No
|
|
| No
| Yes
| No
|
|
| --
| No
| Yes
|
So the problem is to find out if a pattern has any transaction match or root occurrence match.
For frequent-1 patterns, their transaction match or root occurrence match will be evaluated against its super patterns (at least one and at most two) from Frequent-2 set:
- If no super 2-pattern is frequent then it is maximal, else, it is not maximal.
- Transaction support: if no transaction match from super 2-pattern set, then it is closed, otherwise, it is not closed.
- Root occurrence support: if no occurrence match from super 2-pattern set, then it is closed, otherwise, it is not closed.
- Hybrid support, it should not have any match from super 2-pattern set to be closed, if any, it is not closed.
How to determine if a frequent pattern (larger than 1) is NOT closed or NOT maximal?
For any pattern larger than 1, when it's joined (either by connection or combination) with the other parent to generate a child pattern (a super one):
If the child is not frequent, then nothing can be determined.
Else, if this child is frequent, then two things are to be done further:
- First, the parents do have at least one super pattern that is frequent and both of them must not be maximal.
- Secondly, they should be checked, on the basis of required support type, against their child for transaction match and occurrence match so as to determine if they are not closed:
- If transaction support and if it has any match (transaction or root occurrence), then it is not closed.
- If root occurrence support and if it has root occurrence match, then, it is not closed.
- If hybrid support, then any match would make it unclosed.
How to determine if a pattern IS closed?
For a pattern, we can make sure that it is closed if no related match (see the above table) can possibly be discovered and more specifically in CCTreeMiner:
- For root occurrence match, if a pattern which has at least one root occurrence at depth i+1 and after Connection operation at depth i, if its closed property is still unknown (in other word, no root occurrence match has been detected), then no root occurrence match can be discovered further.
- For transaction match, when a pattern is generated to form a super pattern, the match is determined if they have the same transaction support.
How to determine if a pattern IS maximal?
First, for a pattern, we can make sure that it is maximal if no frequent super pattern can possibly be generated further, but how?
Under CCTreeMiner’s mechanism and after each round of Connection at depth i, for a closed pattern which has no super pattern found:
- If transaction support and if the number of its transaction occurrence above i (i is not included) is smaller than threshold, then it is maximal.
- If occurrence support and if the number of its root occurrence above i (i is not included) is smaller than threshold, then it is maximal.
- If hybrid support and if the number of its root occurrence above i (i is not included) is smaller than threshold, then it is maximal.
A problem when mining closed or maximal patterns
Yet, there is a problem when closed or maximal is the case.
Suppose we get two root occurrence matched patterns after combination: F and F' while F' is super to F; Suppose F' is maximal and F has no frequent super pattern except F'. See follows:
F : A,B,C,^,^,D,^,^
F': A,B,C,^,^,D,E,^,^,^
Based on CCTreeMiner’s extension mechanism, F' is generated by a combination between A,B,C,^,^,^ and A,D,E,^,^,^ while F by A,B,C,^,^,^ and A,D,^,^;
Both F and F' will not be able to be extended further. Which is fine for F', it will be marked as closed and maximal if these tasks are required as no super matched pattern nor super frequent pattern can be extended by it. The trouble is that F will also be marked as closed and maximal under the same condition, which is wrong.
Again, this flaw is introduced by the algorithm's inner mechanism of super pattern extension (enumeration among those frequent patterns that have occurrence(s) at the same depth). The way to generate a super pattern by combination is not unique, any two sub patterns can but only one pair is chosen and tested for match.
To compensate, an extra operation has to be added after each round of Combination step for checking ancestor-descendent relationships between those newly combined patterns to prevent this error and thus, a new problem is introduced, that is, determining ancestor-descendent relationship among tree patterns is actually the problem of subtree isomorphism.
Subtree isomorphism
Problem definition: Given trees S and L, find a subtree of L which is isomorphic to S or decide that there is no such subtree.
To be honest, I currently have no idea what is the most efficient algorithm to this problem (again, I use my spare time), partly because the data structure involved (CCTreeMiner adopts preorder representation as the form of pattern tree) and partly because I am not able to find anything valuable in tech-forums (maybe it is not such a common problem that we encounter so often), I write (or implement) an subtree isomorphism algorithm after some observation of my problem. This algorithm is NOT guaranteed to be correct but I also feel that I should be (quite) surprised if it is not.
The algorithm follows a recursively way to do the job and here is a brief description:
The algorithm’s input is the two tree’s preorder lists and the backtrack symbol. It then recursively enumerate the two trees, in a parallel manner, to check and to try to virtually build a list of matched nodes in a sequence that coincides with the smaller tree until a complete match is found or reach a condition that it is not possible for a isomorphic to be exist. Ok, English is not my native and I am sorry for this vague description, just read the code. The related class is SubtreeIsomorphism.
I think this recursive algorithm must have been already introduced somewhere by someone only I don’t know its name. Anyone could inform me?
The time complexity of this method is O(Size(S) * Size(L)). This is far from decent and I’ll come back to improve it when I have time. Anyway, it works now.
Pruning
How to prune patterns that cannot be further generated to create super frequent patterns?
After connection at depth i, for any of those patterns being connected at depth i+1, if its support (transaction or root occurrence or both according to the given support type) above depth i+1 (i+1 is required) does not satisfy threshold(s), then it can be removed as the occurrences bellow depth i will not be able to be further generated (make contribution to a super pattern’s support) and those at and above i are not enough to form any super frequent pattern. The algorithm’s mechanism guarantees this.
How to prune when closed or maximal is the case and frequent is not wanted?
Some times, mining the full set of frequent patterns is simply infeasible but closed or maximal instead. I’ll discuss the reason for a while.
The following pruning method is what I have been able to figure out so far.
The input of each round of Combination at any curtain depth is the set that (only) contains the kind of pattern that: its root has single child and it must have one occurrence at the depth. I call these patterns as seeds (as all frequent patterns which are larger than 2 and have at least one occurrence at the depth can be generated by combining the roots of some of these seed patterns).
A root occurrence of a seed pattern is identified by its root node, yet (as the nature of tree) it may have one to many right most occurrences identified by its rightmost leaf (or leaves).
Pruning strategy: If a seed pattern has any root occurrence match, and the difference between the numbers of their rightmost occurrences is smaller than threshold, then it can be removed.
BTW, occurrences identified by the right most leaf can share the same root, thus breaks Apriori property. That’s why I introduced root based occurrence definition.
Again, why we sometimes need closed or maximal other than frequent?
As I stated in my previous article, it is not feasible to mine the full set of frequent patterns when the size of text trees grows too large.
Let’s see how many induced subtree patterns can possibly contained in a text tree.
Here we denote a tree with root r as Tr.
For an un-empty text tree Tr:
If Tr has only one node, then the upper bound (maximal number) of subtrees contained is 1;
If Tr has more than one node, suppose r has n children (denoted by ri, i=0, 1, … n-1), then Tr’s upper bound is the product of 1 plus (ri can be empty) the number of subtree rooted at ri plus each upper bound of ri.

And the method of calculating the number of subtrees that contains the root is:
If Tr has only one node (the root one), then the number of subtrees contained is 1;
Else, it is:

Tree is very recursive.
Let’s take full binary tree into consideration, see the following.
| Depth | Upper Bound of the Number of Induced Subtrees |
| 1 | 1 |
| 2 | 6 |
| 3 | 37 |
| 4 | 750 |
| 5 | 459,829 |
| 6 | 210,067,308,558 |
| ... | … Really Huge! |
Be aware, this is only the result of induced subtree; it will get much worse when embedded is involved. Now you see why.
BTW, the upper bound happens when every node in the text tree is unique. And there is also a lower bound when every node in a text tree is identical.
The code to calculate the largest number of subtrees is provided and encapsulated in a class named SubTreeNumberPredictor which I use in unit test to check the functionality of mining frequent subtrees.
Hope what I analyzed is correct and hope my code works.
What have been added or changed to this version?
- Tree visualization: you can have a graphic view of a text tree or a pattern tree instead of their preorder string.
- Occurrences visualization: you can have a graphic view of a pattern’s occurrences along with their parasitic text trees.
- A subtree isomorphism algorithm is implemented.
- Bug fixed: some unclosed or un-maximal patterns were wrongly categorized because the previous subtree isomorphism method was not correct.
- Changed structure of CCTreeMiner’s implementation.
- Added some unit tests (Oh! Unit Test! Lift me as a wave, a leaf, a cloud! I fall upon the thorns of BUGs I bleed! :) ).
Well, it spent me countless rest hours to analyze and implement this algorithm as my job is not related with data mining. Yet it pays to see it finally works.
It maybe useful, it may contain bugs, it can be improved and thank you if you point them to me.
