(untagged)

Propagation of Constraints

JorgeLuisOrejel

0.00/5 (No votes)

6 Mar 2015

Propagation of constraints

Download source code - 1.3 MB

Introduction

NOTE: This article is from sections of Chapter 15 “Special Computational Patterns” of my unpublished textbook Applied Algorithms and Data Structures, and is based on the following: Abelson, H., and G.J. Sussman, Structure and Interpretation of Computer Programs, The MIT Press, 1985, pp. 230-242; Sussman, G.J., and G.L. Steele, Jr. “CONSTRAINTS?A Language for Expressing Almost-Hierarchical Descriptions, Artificial Intelligence, Vol. 14, 1980, pp. 1-39; de Kleer, J., and G.J. Sussman. “Propagation of Constraints Applied to Circuit Synthesis,” International Journal of Circuit Theory and Applications, Vol. 8, 1980, pp. 127-144.

This article deals with the implementation of a constraint-propagation system. Computer programs are often organized in terms of one-directional computations, which perform operations on pre-specified arguments to produce desired outputs. On the other hand, systems are modeled in terms of relations among quantities. For example, a mathematical model for a resistor describing its resistance R (in Ohms) is given by the equation R = ρ(L/A), where ρ is the resistivity of the material (in Ohms-cm), L is its length (in cm) and A is its cross-sectional area (in cm squared).

The equation for the resistivity of a material is not one-directional. If any three of the quantities are known, they can be used to compute the fourth. However, translating the equation into a function in a traditional computer language would require choosing one of the quantities to be computed in terms of the other three. Therefore, a procedure for computing the area A could not be used to compute the resistivity ρ, even though both computations arise from the same equation.

Constraint Networks

It is possible to use object-oriented programming to define a new programming language that would allow working in terms of relations. The elements of the new language are primitive constraints, which state that certain relations hold among quantities. For example, the constraint adder( a, b, c ) might specify that the quantities a, b, and c are related by the equation a + b = c. Similarly, the constraint multiplier( u, v, w ) would express the equation u * v = w. To specify constant values for variables, say x == 2.5, we could use a constraint such as constant( x, 2.5 ).

This kind of language provides a means of combining primitive constraints in order to express more complex relations. Constraints are combined by building constraint networks, in which constraints are joined by connectors. A connector is an object that holds a value that may participate in one or more constraints. For example, the relationship between Fahrenheit and Celsius temperatures is given by the equation 9C = 5(F – 32), and such a constraint equation can be thought of as a network of primitive adder, multiplier and constant constraints, as shown below:

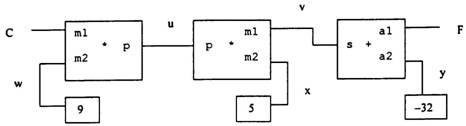
On the left of the figure, there is a multiplier box (i.e., a constraint) with three terminals labeled m1, m2 and p. These connect the multiplier to the rest of the network in the following way. Terminal m1 is linked to a connector C which holds the Celsius temperature. Terminal m2 is linked via connector w to a constant box that holds number 9. Terminal p, which the multiplier box constraints to be the product of m1 and m2, is linked to the p terminal of another multiplier box, whose m2 terminal is connected to a constant box holding 5, while its m1 terminal is connected to the s terminal of an adder box. Terminal a1 of the adder is linked to connector F (holding the Fahrenheit temperature), and terminal a2 is linked to connector y, which in turn is linked to a constant box holding number –32.

The computation by such a network proceeds as follows. When a connector is given a value (either by a User constraint or by a constraint box to which it is linked), it awakens all of its associated constraints (except for the constraint that has been just awakened by the connector) to inform them that it has a value. Each awakened constraint box then polls its connectors to see if there is enough information to determine a value for one of its connectors. If so, the box sets the value of that connector, and the connector awakens all of its associated constraints, thus repeating the process. In the Celsius-Fahrenheit conversion example, connectors w, x and y are immediately set by the constant boxes to 9, 5 and -32, respectively. These connectors awaken the two multipliers and the adder, which determine that there is not enough information to proceed (because connectors C and F, and hence u and v, have no values). When the user constraint (or some other part of the network) sets C to a value, say 25, the leftmost multiplier is awakened and it sets u to the value 25 * 9 = 225. Then, connector u awakens the middle multiplier, which sets v to 45. Finally, connector v awakens the adder, which sets F to 77.

Connectors and Abstract Constraints

The constraint-propagation system can be implemented in C#/C++ via classes, inheritance, and virtual functions. The following declarations constitute the bare minimum that can be used to implement such a system.

public abstract class Constraint              // Abstract constraint
{
   public abstract void ProcessNewValue();    // All processing must be done
   public abstract void ProcessForgetValue(); // by specific (derived) constraints
}

// Constants for message-passing
public enum message { GotValue, LostValue }

// Constants for signaling the type of value held by connectors
public enum valueType { _int, _float }

// Constants to control the output from probes
public enum behavior { normal, quiet }

public class Connector               // A connector
{
   protected string name;            // has a name,
   protected valueType type;         // and holds a certain type of value,
   protected float fvalue;           // either a floating-point value,
   protected int ivalue;             // or an integer value, assigned to it
   protected Constraint informant;   // by an informant (constraint),
   protected List<Constraint> links; // and is linked to other constraints

   // Define and initialize a connector
   public Connector( string str, valueType t )
   {
      name = str;                     // Set the connector's name
      type = t;                       // and its type.
      fvalue = 0F;                    // Clear the value
      ivalue = 0;                     // fields.
      informant = null;               // No constraint has set the connector's value
      links = new List<Constraint>(); // Initialize the list of links
   }

   // Link the connector to a new constraint
   public void Connect( Constraint _newConstraint )
   {
      links.Add( _newConstraint );
      if ( HasValue() )
      {
         try
         {
            _newConstraint.ProcessNewValue();
         }
         catch ( System.Exception e )
         {
            Console.WriteLine( "-- " + e.Message );
         }
      }
   }

   // Tell whether the connector has a value
   public bool HasValue()
   {
      return informant != null;
   }

   // Show the name of the connector
   public void ShowName()
   {
      Console.Write( Name );
   }

   // Properties of the connector

   public string Name    // 'name' property of the connector
   {
      get { return name; }
      set { name = value; }
   }

   public int Ivalue     // 'ivalue' property of the connector
   {
      get { return ivalue; }
   }

   public float Fvalue   // 'fvalue' property of the connector
   {
      get { return fvalue; }
   }

   public valueType Type // 'type' property of the connector
   {
      get { return type; }
   }

   // Special functions to set the ivalue and fvalue fields
   // (too bad the 'setter' of properties cannot take optional
   //  arguments in addition to the implicit 'value' argument)

   // A 'setter' constraint requests the connector to set
   // either its ivalue or its fvalue to a new value

   public void SetValue( int _newValue, Constraint setter )
   {
      if ( !HasValue() )
      {
         ivalue = _newValue;
         informant = setter;
         ForEachExcept( setter, message.GotValue );
      }
      else // HasValue()
         if ( ivalue != _newValue )
         {
            Console.Write( "Connector " );
            ShowName();
            Console.WriteLine( " *** contradiction {0} != {1}",
                               ivalue, _newValue );
         }
   }

   public void SetValue( float _newValue, Constraint setter )
   {
      if ( !HasValue() )
      {
         fvalue = _newValue;
         informant = setter;
         ForEachExcept( setter, message.GotValue );
      }
      else // HasValue()
         if ( fvalue != _newValue )
         {
            Console.Write( "connector " );
            ShowName();
            Console.WriteLine( " *** contradiction {0} != {1}",
                               fvalue, _newValue );
         }
   }

   // A 'retractor' constraint requests the connector
   // to forget its value (either ivalue or fvalue)

   public void ForgetValue( Constraint retractor )
   {
      if ( retractor == informant )
      {
         informant = null;
         ForEachExcept( retractor, message.LostValue );
      }
   }

   // Function to propagate a message among the constraints
   // linked to the connector, except for the constraint
   // that issued the message.

   protected void ForEachExcept( Constraint exception, message m )
   {
      foreach ( Constraint c in links )
      {
         if ( c != exception )
         {
            if ( m == message.GotValue )
            {
               try
               {
                  c.ProcessNewValue();
               }
               catch ( System.Exception e )
               {
                  Console.WriteLine( e.Message );
               }
            }
            else // m == message.LostValue
            {
               c.ProcessForgetValue();
            }
         }
      }
   }
}// Connector (class)

Observe that the class Connector can handle floating-point as well as fixed-point quantities, but not both at the same time. It also has functions to set and retrieve either the int or the float value.

Test of the Constraints Class

The following is a simple test of the ConstraintsLib class:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

using ConstraintsLib;

namespace TestConstraintsLib
{
   class Program
   {
      static void Main( string[] args )
      {
         GenSym sym = new GenSym( "c" );
         Connector c0 = new Connector( sym.next(), valueType._int ),
                   c1 = new Connector( sym.next(), valueType._float );
         Probe p0 = new Probe( c0 ),
               p1 = new Probe( c1 );
         User jlo = new User();

         c0.SetValue( 5, jlo );
         c1.SetValue( 7.3F, jlo );

         c0.SetValue( 8, jlo );     // Should generate a contradiction
         c1.SetValue( 45.4F, jlo ); // Should generate a contradiction

         Console.WriteLine();
         c0.ForgetValue( jlo );
         c1.ForgetValue( jlo );

         Console.WriteLine();
         c0.SetValue( 8, jlo );
         c1.SetValue( 45.4F, jlo );
      }
   }
}

When run as a console application, the output is as follows:

Primitive Constraints

The class Constraint is truly abstract, because it cannot be instantiated. It is not possible to define variables of type Constraint, but other classes can be defined as derived from it. As a simple illustration, an Adder can be defined as a kind of Constraint as follows:

public class Adder : Constraint // An adder is a kind of constraint
{
             // that links to three connectors, two addends (a1, a2)
             // and a sum (s) by means of its constructor,
   protected Connector a1, a2, s;
   protected Report report = new Report();

   public Adder( Connector _1, Connector _2, Connector _3 )
   {
      a1 = _1;            // Maintain a reference to each of
      a2 = _2;            // the connectors associated to
      s = _3;             // the constraint.
      a1.Connect( this ); // Link (i.e., connect) each of the
      a2.Connect( this ); // connectors to this constraint
      s.Connect( this );  // (instance of adder).

      report._3argConstraint( "Adder", _1, _2, _3 );
   }

   // Provide specific implementations of the
   // virtual functions of the base abstract class

   public override void ProcessNewValue()
   {
      // If any two connectors have a value, set the value of the third

      bool a1Hv = a1.HasValue(), a2Hv = a2.HasValue(), sHv = s.HasValue();

      if ( s.Type == valueType._float )
      {
         float sV = s.Fvalue, a1v = a1.Fvalue, a2v = a2.Fvalue;

         if ( a1Hv && a2Hv ) s.SetValue( a1v + a2v, this );
         else
            if ( a1Hv && sHv ) a2.SetValue( sV - a1v, this );
            else
               if ( a2Hv && sHv ) a1.SetValue( sV - a2v, this );
      }
      else // s.Type == valueType._int
      {
         int sV = s.Ivalue, a1v = a1.Ivalue, a2v = a2.Ivalue;

         if ( a1Hv && a2Hv ) s.SetValue( a1v + a2v, this );
         else
            if ( a1Hv && sHv ) a2.SetValue( sV - a1v, this );
            else
               if ( a2Hv && sHv ) a1.SetValue( sV - a2v, this );
      }
   }

   public override void ProcessForgetValue()
   {
      s.ForgetValue( this );  // Inform the three connectors
      a1.ForgetValue( this ); // that this constraint requests
      a2.ForgetValue( this ); // them to forget their values.
      ProcessNewValue();      // Try to process a new value
   }                          // not originally set by adder.
}// Adder (class)

The definition of the Adder constraint provides specific implementations of the virtual functions of the abstract base class. Function ProcessNewValue is called when the adder is informed that one of its connectors has a value. For simplicity, the function assumes that the connectors linked to the adder hold the same type of value. By inspecting the type of value held by connector s, the appropriate functions can be called to get and set connector values.

Function ProcessForgetValue is called when the adder is informed that one of its connectors has lost its value. The function requests all the connectors linked to the adder to forget their values. (Only the values originally set by this adder are actually lost). Then it calls ProcessNewValue because one or more of the connectors may still have a value (not originally set by the adder) that must be propagated through other constraints.

A Multiplier constraint can be defined in a way similar to that of an adder, with the provision that the multiplier will set its product to zero if either of the factors is zero, even if the value of the other factor is not known (undefined). The definition of the class Multiplier is a similar class. In the case of division by zero, function ProcessNewValue for the Multiplier constraint must abort the execution of the program that makes use of the multiplier constraint.

A Constant constraint simply sets the value of its associated connector. The two constructors allow defining floating-point and fixed-point constants. Its member functions ProcessNewValue and ProcessForgetValue do not perform any action (because constants do not change).

public class Constant : Constraint // A constant is a kind of constraint,
{
   protected Connector conn;       // linked to a connector by its constructors,

   public Constant( float f, Connector c )
   {
      conn = c;                 // Set reference to the connector.
      conn.Connect( this );     // Link (i.e., connect) the connector.
      conn.SetValue( f, this ); // Set the fvalue field.
   }

   public Constant( int i, Connector c )
   {
      conn = c;                 // Set reference to the connector.
      conn.Connect( this );     // Link (i.e., connect) the connector.
      conn.SetValue( i, this ); // Set the ivalue field.
   }

   public override void ProcessNewValue() { }    // No actions are performed
   public override void ProcessForgetValue() { } // because constants do not change
}// Constant (class)

Creation and Linkage of Connectors

The constructor of the Connector class must initialize the name of a connector, set its informant to zero (to indicate that the connector has no value), and initialize the list of links to constraints. When function Connector.Connect is called by a constraint, the reference to the constraint must be added to the list of links of the connector. Then, if the connector has a value, the constraint must process such a value.

Message-Passing Among Connectors and Constraints

Connectors communicate with constraints by passing messages to them via the enumerated type message, defined as follows:

// Constants for message-passing
public enum message { GotValue, LostValue }

A connector uses the message GotValue to signal to a constraint that it has acquired a new value, and the message LostValue to signal that it has lost its value. A connector’s SetFvalue or SetIvalue function is called to request the setting of its value. If the connector does not have a value, it sets the value and remembers as the informant the constraint that requested the setting of the value. Then, the connector sends a message about the new value to all the constraints linked to it except the constraint that requested the value to be set. These actions for the case of floating-point values are implemented by the following code:

public void SetValue( float _newValue, Constraint setter )
 {
    if ( !HasValue() )
    {
       fvalue = _newValue;
       informant = setter;
       ForEachExcept( setter, message.GotValue );
    }
    else // HasValue()
       if ( fvalue != _newValue )
       {
          Console.Write( "connector " );
          ShowName();
          Console.WriteLine( " *** contradiction {0} != {1}",
                             fvalue, _newValue );
       }
 }

The definition of function SetIvalue is similar.

Function ForEachExcept is defined as follows:

// Function to propagate a message among the constraints
// linked to the connector, except for the constraint
// that issued the message.

protected void ForEachExcept( Constraint exception, message m )
{
   foreach ( Constraint c in links )
   {
      if ( c != exception )
      {
         if ( m == message.GotValue )
         {
            try
            {
               c.ProcessNewValue();
            }
            catch ( System.Exception e )
            {
               Console.WriteLine( e.Message );
            }
         }
         else // m == message.LostValue
         {
            c.ProcessForgetValue();
         }
      }
   }
}

If a retractor constraint calls function Connector::ForgetValue to request a connector to forget its value, the connector first makes sure that the request comes from the same constraint that set the value originally. If that is not the case, the connector ignores the request. Otherwise, the connector clears the informant reference, and informs its associated constraints (except the retractor) about the loss of its value. The definition of function Connector::ForgetValue is as follows:

// A 'retractor' constraint requests the connector
// to forget its value (either ivalue or fvalue)

 public void ForgetValue( Constraint retractor )
 {
    if ( retractor == informant )
    {
       informant = null;
       ForEachExcept( retractor, message.LostValue );
    }
 }

Probes and Users

In order to watch a constraint network in action, probes can be attached to connectors. A Probe constraint prints an appropriate message (via ProcessNewValue and ProcessForgetValue, respectively) about the setting or unsetting of the value of the associated connector. Additionally, the user of the constraint-propagation system may want to set/unset the values on one or more connectors. For this purpose, it is convenient to define a dummy constraint User (whose constructor, ProcessNewValue and ProcessForgetValue functions do nothing) that could be passed as either the setter or the retractor argument to the SetFvalue, SetIvalue, and ForgetValue functions of connectors. The definition of the constraints Probe and User are as follows:

public class Probe : Constraint // A probe is a kind of constraint,
{
   protected Connector conn;         // linked to a connector by its constructor.
   protected behavior onForgetValue; // output normal or quiet

   public Probe( Connector c, behavior ofg = behavior.normal )
   {
      conn = c;             // Maintain a reference to the connector.
      conn.Connect( this ); // Link (i.e., connect) the connector.
      onForgetValue = ofg;
   }

   public override void ProcessNewValue()    // Print the new value assigned
   {                                         // to a connector
      Console.Write( "probe: " );
      conn.ShowName();
      if ( conn.Type == valueType._float )
      {
         Console.WriteLine( "(f) = {0}", conn.Fvalue );
      }
      else // conn.Type == valueType._int
      {
         Console.WriteLine( "(i) = {0}", conn.Ivalue );
      }
   }

   public override void ProcessForgetValue()  // Print a '?' to signal that
   { //                                       // a connector has lost its value
      if ( onForgetValue == behavior.normal )
      {
         Console.Write( "\tprobe: " );
         conn.ShowName();
         Console.WriteLine( " = ?" );
      }
   }
}// Probe (class)

public class User : Constraint // A user is a kind of constraint
{
   public User() { }                             // Associated to nothing,
   public override void ProcessNewValue() { }    // and performing
   public override void ProcessForgetValue() { } // no actions
}// User (class)

Generic Primitive Logic Gates

A simple application of connectors that hold integer values is the implementation of generic primitive logic gates. The following figure illustrates the symbols for the primitive logic functions NOT, AND, and OR, respectively.

An inverter is a logic gate with one input and one output (the connector emerging from the small circle). The NOT function prescribes that the (logic) value on the output connector is the complement of the value on the input connector, that is, if the input is 0(1) the output is 1(0).

The two-input, one-output AND gate produces a 1 on its output connector only when both input connectors hold a 1, while the output is 0 whenever one (or both) of the inputs is (are) 0. The output of an OR gate is 0 only when both of its inputs are 0, while the output is 1 whenever one (or both) of the inputs is (are) 1. These operational descriptions can be easily implemented by constraints. However, suppose that it is desired to implement N-input, 1-output AND and OR logic gates, with the additional requirement that the number of inputs is to be determined at run time. In combination with the inverter, such gates are extremely useful as building blocks to implement logic circuits of arbitrary complexity.

Instead of plunging into a straightforward implementation of these gates as two different kinds of constraints, some thought reveals that they share common features. In both cases, it is necessary to (a) keep track of the actual number of connectors, (b) allocate references to the connectors, (c) initialize the references, and (d) link the connectors to the constraint. Further thought reveals that, no matter what kind of logic function is performed, in both cases function ProcessForgetValue must do the same, namely tell all the connectors associated with the constraint to forget their values. By exploiting the inheritance mechanism of C# the AND and OR gates can be implemented as specializations of a generic N-input, 1-output logic gate (NinGate) defined as follows:

public class NinGate : Constraint // An N-input, 1-output gate
{                                 // is a kind of constraint
   protected int M;               // with a number (M) of external connectors
                                  // which is determined at run time.
                                  // Connectors 0 .. M-2 are the N inputs
                                  // and connector M-1 is the output.
   protected Connector[] conn;
   protected Report report = new Report();

   public NinGate( params Connector[] _c )
   {
      M = _c.Length;
      conn = new Connector[ M ];
      for ( int i = 0; i < M; ++i )
      {
         conn[ i ] = new Connector( "_", valueType._int ); // Anonymous instance
                                                           // of a connector
         conn[ i ] = _c[ i ]; // Maintain a reference to each connector.
      }
      for ( int i = 0; i < M; ++i )
      {
         conn[ i ].Connect( this ); // Link (i.e., connect) each connector to
      }                             // this constraint (instance of NinGate).
   }

   public override void ProcessForgetValue() // Can be implemented at this level
   {
      for ( int i = 0; i < M; ++i )     // Inform each connector that this
      {                                 // constraint requests them to forget
         conn[ i ].ForgetValue( this ); // their values.
      }
      ProcessNewValue();                // Try to process a new value not
   }                                    // originally set by NinGate.

   public override void ProcessNewValue() // No processing can be performed
   {                                      // without further specialization
   }                                      // (i.e., kind of gate implemented)
}// NinGate (class)

Observe that the class NinGate provides an implementation of ProcessForgetValue, but maintains as pure virtual the function ProcessNewValue.

The specializations of an NinGate into AND and OR gates involve the implementation of function ProcessNewValue for each gate. Thus, an N-input, 1-output AND gate (NinAnd) can be defined as a kind of NinGate as follows:

public class NinAnd : NinGate // An NinAnd gate is a kind of NinGate
{
   public NinAnd( params Connector[] _c )
          :
          base( _c ) { report.NargConstraint( "And", _c ); }

   public override void ProcessNewValue() // that processes new values according
   {                                      // to the logic of the AND function.
      int i, withValue, M1 = M - 1;

      for ( i = 0, withValue = 0; i < M1; ++i )
      {
         if ( conn[ i ].HasValue() )
         {
            ++withValue;
            if ( conn[ i ].Ivalue == 0 )
            {
               conn[ M1 ].SetValue( 0, this ); // when any input is 0
               return;                         // the output must be 0
            }
         }
      }
      if ( withValue == M1 ) // when all inputs are 1
      {
         conn[ M1 ].SetValue( 1, this ); // the output must be 1
      }
      else
         if ( conn[ M1 ].HasValue() && conn[ M1 ].Ivalue == 1 ) // when the output is 1
         {
            for ( i = 0; i < M1; ++i )
            {
               conn[ i ].SetValue( 1, this ); // all inputs must be 1
            }
         }
   }
}// NinAnd (class)

An N-input, 1-output OR gate (NinOr) is defined in a similar way.

Conservative-Logic Fredkin Gates

This section and the next deal with further extensions to the constraint-propagation system to implement conservative-logic circuits. (After Fredkin, E., and T. Toffoli “Conservative Logic,” International Journal of Theoretical Physics, Vol. 21, No. 3, 1982, pp. 227-230. More accessible descriptions of Fredkin gates can be found in the following books: Hey, T., and R.W. Allen (Eds.) Feynman Lectures on Computation, Westview, 1999, pp. 34-39. Feynman, R.P. The Pleasure of finding things out, Cambridge, Massachusetts: Perseus Books, pp. 40-41. Milburn, G.J. The Feynman Processor: Quantum Entanglement and the Computing Revolution, Australia: Perseus Books, 1998, pp. 125-131.)

The Fredkin gate is a computing element that allows reversible computation, and has received much attention for quantum computation. This gate (illustrated below) performs conditional crossover of two data signals according to the value of a control signal.

When the control signal (u) is 1, the two data signals follow parallel paths; when the control signal is 0, the two data signals cross over. Observe that this gate is nonlinear. When considered as a function, the gate coincides with its own inverse, that is, two Fredkin gates connected in cascade yield the identity function:

The following figures illustrate my CMOS implementation of the Fredkin gate in terms of both transmission gates and a basic inverter (which is used to generate the complement of the control signal u). This is to show that this gate is not just a mathematical toy.

CMOS Fredkin gate	Basic CMOS inverter

The implementation of a Fredkin gate in terms of a constraint-propagation system is as follows:

using ConstraintsLib;

namespace FredkinGate
{
   public class FredkinGate : Constraint // A Fredkin gate is a kind of constraint
   {
      protected Connector[] conn; // that links to several connectors by means of its constructor

      public FredkinGate( Connector[] _c ) // elements of array _c: u, v, x1, x2, y1, y2
      {
         conn = new Connector[ Constants.FGn2 ]; // elements of array conn: u, v, x1, x2, y1, y2

         Console.Write( "FredkinGate( " );
         for ( int i = 0; i < Constants.FGn2; ++i )
         {
            conn[ i ] = _c[ i ];
            conn[ i ].Connect( this );
            conn[ i ].ShowName();
            Console.Write( " " );
         }
         Console.WriteLine( " )" );
      }

      protected void TrySetSignals( int uv )
      {
         for ( int i = 2; i < Constants.FGn2; ++i )
         {
            if ( conn[ i ].HasValue() )
            {
               conn[ (int)Constants.FGlut[ uv, i ] ].SetValue( conn[ i ].Ivalue, this );
            }
         }
      }

      public override void ProcessNewValue()
      {
         int u, v;

         if ( conn[ (int)SI._u ].HasValue() )
         {
            u = conn[ (int)SI._u ].Ivalue;
            conn[ (int)SI._v ].SetValue( u, this );
            TrySetSignals( u );
         }
         else // !conn[ (int)SI._u ].HasValue()
         {
            if ( conn[ (int)SI._v ].HasValue() )
            {
               v = conn[ (int)SI._v ].Ivalue;
               conn[ (int)SI._u ].SetValue( v, this );
               TrySetSignals( v );
            }
         }
      }

      public override void ProcessForgetValue()
      {
         for ( int i = 0; i < Constants.FGn2; ++i )
         {
            conn[ i ].ForgetValue( this );
         }
         ProcessNewValue();
      }
   }
}

Conservative-Logic Primitive Functions

The Fredkin gate can be used to implement (as constraints) the primitive logic functions NOT, AND, and OR illustrated below:

NOT	AND	OR

As an example, the following code implements a conservative-logic AND function in terms of a Fredkin gate:

using ConstraintsLib;

namespace FredkinGate
{
   public class ConsLogic_AND : Constraint
   {
      protected Connector[] conn;       // ConsLogic_AND gate I/O connectors (a, b, ab)
      protected Connector[] FG_IO_Conn; // Fredkin gate I/O connectors (u, v, x1, x2, y1, y2)
      protected Constant zero;          // Constant 0 fed to Fredkin gate input x2
      protected FredkinGate fg;         // Fredkin gate

      public ConsLogic_AND( Connector[] _c ) // elements of array _c: a, b, ab
      {
         // Link the input/output connectors

         conn = new Connector[ 3 ]; // elements of array conn: a, b, ab
         Console.Write( "ConsLogic_ANDgate( " );
         for ( int i = 0; i < 3; ++i )
         {
            conn[ i ] = _c[ i ];
            conn[ i ].Connect( this );
            conn[ i ].ShowName();
            Console.Write( " " );
         }
         Console.WriteLine( " )" );

         // Implement the conservative-logic AND gate

         FG_IO_Conn = new Connector[ Constants.FGn2 ];

         FG_IO_Conn[ 0 ] = conn[ 0 ]; // a <--> u
         FG_IO_Conn[ 1 ] = conn[ 0 ]; // a <--> v
         FG_IO_Conn[ 2 ] = conn[ 1 ]; // b <--> x1

         FG_IO_Conn[ 3 ] = new Connector( "0", valueType._int );
         zero = new Constant( 0, FG_IO_Conn[ 3 ] );              // 0 <--> x2

         FG_IO_Conn[ 4 ] = conn[ 2 ]; // ab <--> y1
         FG_IO_Conn[ 5 ] = new Connector( "_ab", valueType._int );

         fg = new FredkinGate( FG_IO_Conn );
      }

      public override void ProcessNewValue() { }    // all the work is done by the Fredkin gate

      public override void ProcessForgetValue() { } // all the work is done by the Fredkin gate
   }
}

Upon execution as a Console application, the output is as follows:

Complex Logic Building Blocks

The primitive logic functions that have been implemented as constraints can be further combined to create more complex building blocks. As a simple and interesting example, the constraint-propagation system can be used to implement a 4-to-1-line multiplexer similar to the Transistor-Transistor Logic (TTL) SN74153 4-to-1 multiplexer, whose internal logic and block diagram are shown below. (After Texas Instruments Inc. The TTL Data Book for Design Engineers, Dallas, Texas, 1976.)

One half of the TTL SN74153 4-to-1 multiplexer and its block diagram

Using N-input, 1-output AND/OR gates, one-half of the SN74153 multiplexer is implemented as follows:

using ConstraintsLib;
using NinGatesLib;

namespace HalfSN74153
{
   // Input/Ouput signals for the multiplexer

   public enum h74153signal { G, C0, C1, C2, C3, B, A, Y };

   public class H_SN74153 : Constraint // One half of an SN74153 is a kind
   {                                   // of constraint, implemented with
      protected Connector[] w,         // five level-1, level-2 internal connectors,
                            x;         // four level-3 internal connectors,
      protected Inverter[] inv;        // five inverters,
      protected NinAnd[] and;          // four 4-input AND gates,
      protected NinOr or;              // and one 4-input OR gate

      protected Report report = new Report();

      public H_SN74153( params Connector[] extC )
      {
         // extC.Length == 8
         // Array extC contains the external I/O connectors to interface
         // with the multiplexer, indexed by the h74153signal enumeration.

         GenSym wSym = new GenSym( "w" ), // symbol-generator for level-1 and level-2 connectors
                xSym = new GenSym( "x" ); // symbol-generator for level-3 connectors
         int i;

         // Create the internal connectors
         w = new Connector[ 5 ];
         x = new Connector[ 4 ];
         for ( i = 0; i < 4; ++i )
         {
            w[ i ] = new Connector( wSym.next(), valueType._int );
            x[ i ] = new Connector( xSym.next(), valueType._int );
         }
         w[ 4 ] = new Connector( wSym.next(), valueType._int );

         // Create the inverters
         inv = new Inverter[ 5 ];
         inv[ 0 ] = new Inverter( extC[ (int)h74153signal.G ], w[ 0 ] );
         inv[ 1 ] = new Inverter( extC[ (int)h74153signal.B ], w[ 1 ] );
         inv[ 2 ] = new Inverter( w[ 1 ], w[ 3 ] );
         inv[ 3 ] = new Inverter( extC[ (int)h74153signal.A ], w[ 2 ] );
         inv[ 4 ] = new Inverter( w[ 2 ], w[ 4 ] );

         // Create AND gates
         and = new NinAnd[ 4 ];
         and[ 0 ] = new NinAnd( w[ 0 ], w[ 1 ], w[ 2 ], extC[ (int)h74153signal.C0 ], x[ 0 ] );
         and[ 1 ] = new NinAnd( w[ 0 ], w[ 1 ], w[ 4 ], extC[ (int)h74153signal.C1 ], x[ 1 ] );
         and[ 2 ] = new NinAnd( w[ 0 ], w[ 3 ], w[ 2 ], extC[ (int)h74153signal.C2 ], x[ 2 ] );
         and[ 3 ] = new NinAnd( w[ 0 ], w[ 3 ], w[ 4 ], extC[ (int)h74153signal.C3 ], x[ 3 ] );

         // create OR gate
         or = new NinOr( x[ 0 ], x[ 1 ], x[ 2 ], x[ 3 ], extC[ (int)h74153signal.Y ] );

         report.NargConstraint( "Half SN74153", extC );
      }

      public override void ProcessNewValue() { }    // All the processing is done
      public override void ProcessForgetValue() { } // by the internal gates

   }// H_SN74153 (class)
}

The 4-to-1 multiplexer can be used as a building block for a 4-bit, left-shift, barrel shifter whose implementation is shown below. The shifter has two control inputs (A and B), four parallel inputs (I0 to I3), a “fill” input (F), and four parallel outputs (Y0 to Y3). The most significant data bits are I3 and Y3, while B is the most significant control bit.

As a test of the barrel shifter, the input bits 1001 from the parallel inputs can be transferred to the outputs, and shifted to the left by generating all the possible combinations of the control inputs and of the fill input.

namespace FourBitBarrelShifter
{
   class Program
   {
      static void Main( string[] args )
      {
         GenSym iSym = new GenSym( "I" ),                    // symbol-generator for input (I) connectors
                ySym = new GenSym( "Y" );                    // symbol-generator for output (Y) connectors
         Connector[] i = new Connector[ 4 ],                 // connectors for input signals
                     y = new Connector[ 4 ];                 // connectors for output signals
         Connector f = new Connector( "F", valueType._int ), // connector for fill signal
                   g = new Connector( "G", valueType._int ), // connector for gate control
                   a = new Connector( "A", valueType._int ), // connector for address signal A
                   b = new Connector( "B", valueType._int ); // connector for address signal B
         Constant gnd = new Constant( 0, g );                // gate control connected to ground
         Probe[] pr = new Probe[ 7 ];                        // probes for the F, and A-B and Y connectors
         H_SN74153[] mux = new H_SN74153[ 4 ];               // 4 half SN74153 multiplexers
         User jlo = new User();                              // user constraint to set/clear signals
         int j, k;

         // Create the input-output connectors
         for ( j = 0; j < 4; ++j )
         {
            i[ j ] = new Connector( iSym.next(), valueType._int );
            y[ j ] = new Connector( ySym.next(), valueType._int );
         }

         // Create the probes
         j = k = 0;
         while ( j < 4 ) // for the output connectors
         {
            pr[ j++ ] = new Probe( y[ k++ ], behavior.quiet );
         }
         pr[ j++ ] = new Probe( f );
         pr[ j++ ] = new Probe( a, behavior.quiet );
         pr[ j++ ] = new Probe( b, behavior.quiet );

         // Sample input signals
         i[ 3 ].SetValue( 1, jlo );
         i[ 2 ].SetValue( 0, jlo );
         i[ 1 ].SetValue( 0, jlo );
         i[ 0 ].SetValue( 1, jlo );

         // Create the multiplexers
         //
         // Mux signals: G, C0, C1, C2, C3, B, A, Y

         mux[ 3 ] = new H_SN74153( g, i[ 3 ], i[ 2 ], i[ 1 ], i[ 0 ], b, a, y[ 3 ] );
         mux[ 2 ] = new H_SN74153( g, i[ 2 ], i[ 1 ], i[ 0 ], f,      b, a, y[ 2 ] );
         mux[ 1 ] = new H_SN74153( g, i[ 1 ], i[ 0 ], f,      f,      b, a, y[ 1 ] );
         mux[ 0 ] = new H_SN74153( g, i[ 0 ], f,      f,      f,      b, a, y[ 0 ] );

         for ( int _f = 0; _f < 2; ++_f )
         {
            f.SetValue( _f, jlo );
            for ( int _a = 0; _a < 2; ++_a )
            {
               a.SetValue( _a, jlo );
               for ( int _b = 0; _b < 2; ++_b )
               {
                  Console.WriteLine( String.Format( "\nF = {0}, A = {1}, B = {2}\n", _f, _a, _b ) );
                  b.SetValue( _b, jlo );
                  b.ForgetValue( jlo );
               }
               a.ForgetValue( jlo );
            }
            f.ForgetValue( jlo );
         }
      }
   }
}

When run as a console application, excerpts of the output are as follows:

Running the Code

To run the code, unzip the Projects file into your Visual Studio Projects directory.

License

This article has no explicit license attached to it but may contain usage terms in the article text or the download files themselves. If in doubt please contact the author via the discussion board below.

A list of licenses authors might use can be found here