Introduction
The Data Encryption Standard (DES) is a block cipher (a form of shared secret encryption) that was selected by the National Bureau of Standards as an official Federal Information Processing Standard (FIPS) for the United States in 1976 and which has subsequently enjoyed widespread use internationally. It is based on a symmetric-key algorithm that uses a 56-bit key. The algorithm was initially controversial with classified design elements, a relatively short key length, and suspicions about a National Security Agency (NSA) backdoor. DES consequently came under intense academic scrutiny, which motivated the modern understanding of block ciphers and their cryptanalysis.
DES is now considered to be insecure for many applications. This is chiefly due to the 56-bit key size being too small; in January 1999, distributed.net and the Electronic Frontier Foundation collaborated to publicly break a DES key in 22 hours and 15 minutes. There are also some analytical results which demonstrate theoretical weaknesses in the cipher, although they are infeasible to mount in practice. The algorithm is believed to be practically secure in the form of Triple DES, although theoretical attacks are possible. In recent years, the cipher has been superseded by the Advanced Encryption Standard (AES).
Furthermore, DES has been withdrawn as a standard by the National Institute of Standards and Technology (formerly the National Bureau of Standards). [Wikipedia]
Simplified DES, developed by Professor Edward Schaefer of Santa Clara University, is an educational rather than a secure encryption algorithm. It has similar properties and structure to DES, with much smaller parameters.
In this article, we will use SDES to encrypt and decrypt binary files.
Background
Figure C.1 illustrates the overall structure of the simplified DES, which we will refer to as SDES. The S-DES encryption algorithm takes an 8-bit block of plaintext (example: 10111101) and a 10-bit key as input, and produces an 8-bit block of ciphertext as output. The S-DES decryption algorithm takes an 8-bit block of ciphertext and the same 10-bit key used to produce that ciphertext as input, and produces the original 8-bit block of plaintext.
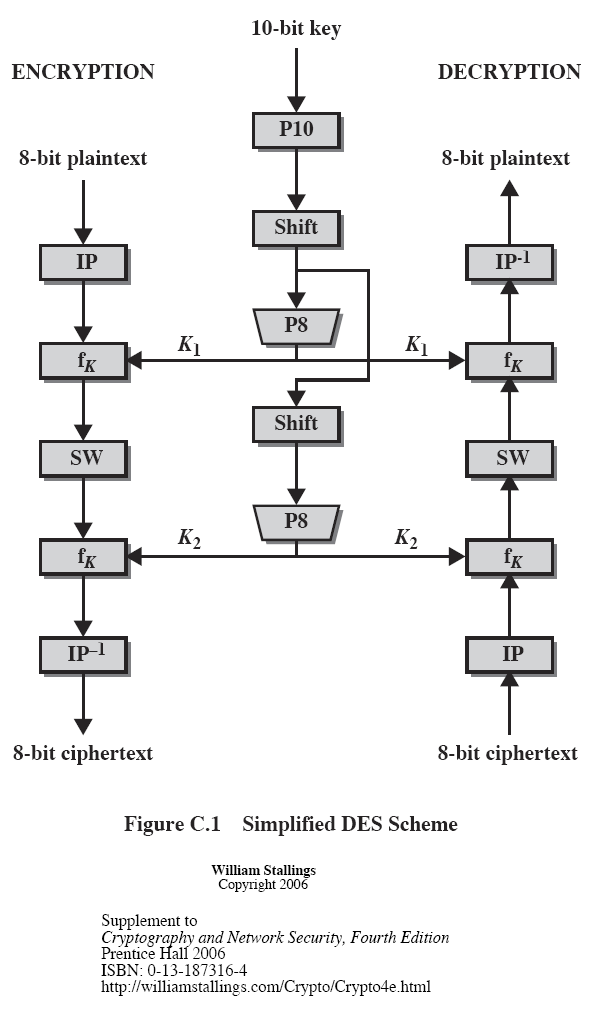
The encryption algorithm involves five functions: an initial permutation (IP); a complex function labeled fK, which involves both permutation and substitution operations and depends on a key input; a simple permutation function that switches (SW) the two halves of the data; the function fK again; and finally, a permutation function that is the inverse of the initial permutation (IP-1). The use of multiple stages of permutation and substitution results in a more complex algorithm, which increases the difficulty of cryptanalysis. The function fK takes as input not only the data passing through the encryption algorithm, but also an 8-bit key. The algorithm could have been designed to work with a 16-bit key, consisting of two 8-bit subkeys, one used for each occurrence of fK. Alternatively, a single 8-bit key could have been used, with the same key used twice in the algorithm. A compromise is to use a 10-bit key from which two 8-bit subkeys are generated, as depicted in Figure C.1. In this case, the key is first subjected to a permutation (P10). Then a shift operation is performed. The output of the shift operation then passes through a permutation function that produces an 8-bit output (P8) for the first subkey (K1). The output of the shift operation also feeds into another shift and another instance of P8 to produce the second subkey (K2). We can concisely express the encryption algorithm as a composition of functions:

Using the Code
Step 1: S-DES Key Generation
S-DES depends on the use of a 10-bit key shared between the sender and the receiver. From this key, two 8-bit subkeys are produced for use in particular stages of the encryption and decryption algorithm. The above figure depicts the stages followed to produce the subkeys. First, permute the key in the following fashion. Let the 10-bit key be designated as (k1, k2, k3, k4, k5, k6, k7, k8, k9, k10). Then the permutation P10 is defined as: P10(k1, k2, k3, k4, k5, k6, k7, k8, k9, k10) = (k3, k5, k2, k7, k4, k10, k1, k9, k8, k6).
176
177 BitArray P10(BitArray key)
178 {
179
180
181 BitArray permutatedArray = new BitArray(10);
182
183 permutatedArray[0] = key[2];
184 permutatedArray[1] = key[4];
185 permutatedArray[2] = key[1];
186 permutatedArray[3] = key[6];
187 permutatedArray[4] = key[3];
188 permutatedArray[5] = key[9];
189 permutatedArray[6] = key[0];
190 permutatedArray[7] = key[8];
191 permutatedArray[8] = key[7];
192 permutatedArray[9] = key[5];
193
194 return permutatedArray;
195 }
Next, we apply P8, which picks out and permutes 8 of the 10 bits according to the following:
rule: P8
P8(1 2 3 4 5 6 7 8 9 10) = (6 3 7 4 8 5 10 9 )
We then go back to the pair of 5-bit strings produced by the two LS-1 functions and perform a circular left shift of 2 bit positions on each string.
289 BitArray Circular_left_shift(BitArray a, int bitNumber)
290 {
291 BitArray shifted = new BitArray(a.Length);
292 int index = 0;
293 for (int i = bitNumber; index < a.Length; i++)
294 {
295 shifted[index++] = a[i%a.Length];
296 }
297 return shifted;
298 }
299
Step 2: S-DES Encryption
2.a Initial and Final Permutations
The input to the algorithm is an 8-bit block of plaintext, which we first permute using the IP function: IP(1 2 3 4 5 6 7 8) = (2 6 3 1 4 8 5 7).
251
252 BitArray IP(BitArray plainText)
253 {
254
255
256 BitArray permutatedArray = new BitArray(8);
257
258 permutatedArray[0] = plainText[1];
259 permutatedArray[1] = plainText[5];
260 permutatedArray[2] = plainText[2];
261 permutatedArray[3] = plainText[0];
262 permutatedArray[4] = plainText[3];
263 permutatedArray[5] = plainText[7];
264 permutatedArray[6] = plainText[4];
265 permutatedArray[7] = plainText[6];
266
267 return permutatedArray;
268 }
This retains all 8 bits of the plaintext, but mixes them up. At the end of the algorithm, the inverse permutation is used: IP inverse(1 2 3 4 5 6 7 8) = (4 1 3 5 7 2 8 6).
270 BitArray RIP(BitArray permutedText)
271 {
272
273
274
275 BitArray permutatedArray = new BitArray(8);
276
277 permutatedArray[0] = permutedText[3];
278 permutatedArray[1] = permutedText[0];
279 permutatedArray[2] = permutedText[2];
280 permutatedArray[3] = permutedText[4];
281 permutatedArray[4] = permutedText[6];
282 permutatedArray[5] = permutedText[1];
283 permutatedArray[6] = permutedText[7];
284 permutatedArray[7] = permutedText[5];
285
286 return permutatedArray;
287 }
2.b The Function fK
The most complex component of S-DES is the function fK, which consists of a combination of permutation and substitution functions. The functions can be expressed as follows. Let L and R be the leftmost 4 bits and rightmost 4 bits of the 8-bit input to fK, and let F be a mapping (not necessarily one to one) from 4-bit strings to 4-bit strings. Then we let:

337 BitArray Fk(BitArray IP, BitArray key)
338 {
339 BitArray[] temp = Split_Block(IP);
340 BitArray Left = Xor(temp[0], F(temp[1], key));
341 BitArray joined = new BitArray(8);
342 int index = 0;
343 for (int i = 0; i < 4; i++)
344 {
345 joined[index++] = Left[i];
346 }
347 for (int i = 0; i < 4; i++)
348 {
349 joined[index++] = temp[1][i];
350 }
351 return joined;
352 }

232 BitArray EP(BitArray input)
233 {
234
235
236
237 BitArray permutatedArray = new BitArray(8);
238
239 permutatedArray[0] = input[3];
240 permutatedArray[1] = input[0];
241 permutatedArray[2] = input[1];
242 permutatedArray[3] = input[2];
243 permutatedArray[4] = input[1];
244 permutatedArray[5] = input[2];
245 permutatedArray[6] = input[3];
246 permutatedArray[7] = input[0];
247
248 return permutatedArray;
249 }
2.c The S-box
The first 4 bits (first row of the preceding matrix) are fed into the S-box S0 to produce a 2-bit output, and the remaining 4 bits (second row) are fed into S1 to produce another 2-bit output. These two boxes are defined as follows:

The S-boxes operate as follows. The first and fourth input bits are treated as a 2-bit number that specify a row of the S-box, and the second and third input bits specify a column of the Sbox. The entry in that row and column, in base 2, is the 2-bit output.
318 BitArray S_Boxes(BitArray input, int no)
319 {
320 BitArray[,] current_S_Box;
321
322 if (no == 1)
323 current_S_Box = S_Box1;
324 else
325 current_S_Box = S_Box2;
326
327 return current_S_Box[binstr2decimal(bin2str(input[0]) + bin2str(input[3])),
328 binstr2decimal(bin2str(input[1]) + bin2str(input[2]))];
329 }
Next, the 4 bits produced by S0 and S1 undergo a further permutation as follows: P4(1 2 3 4) = (2 4 3 1).
The output of P4 is the output of the function F.
331 BitArray F(BitArray right, BitArray sk)
332 {
333 BitArray[] temp = Split_Block(Xor(EP(right), sk));
334 return P4(S_Boxes(temp[0], 1), S_Boxes(temp[1], 2));
335 }
2.d The Switch Function
The function fK only alters the leftmost 4 bits of the input. The switch function (SW) interchanges the left and right 4 bits so that the second instance of fK operates on a different 4 bits. In this second instance, the E/P, S0, S1, and P4 functions are the same. The key input is K2.
354 BitArray Switch(BitArray input)
355 {
356 BitArray switched = new BitArray(8);
357 int index = 0;
358 for (int i = 4; index < input.Length; i++)
359 {
360 switched[index++] = input[i%input.Length];
361 }
362 return switched;
363 }
2.e Finally, Putting Them All in the Encryption and Decryption Process
84 public byte Encrypt(byte block)
85 {
86 BitArray bits_block = byte2bits(block);
87 BitArray[] keys = Generate_Keys();
88 return bits2byte(RIP(Fk(Switch(Fk(IP(bits_block), keys[0])), keys[1])));
89
90 }
91
92 public byte Decrypt(byte block)
93 {
94 BitArray bits_block = byte2bits(block);
95 BitArray[] keys = Generate_Keys();
96 return bits2byte(RIP(Fk(Switch(Fk(IP(bits_block), keys[1])), keys[0])));
97
98 }
Step 3: Using S-DES for Encryption and Decryption of Binary Files
3.a Encryption Process
116 private void Encrypt()
117 {
118 FileStream fs = new FileStream(txt_enc_in.Text, FileMode.Open);
119 BinaryReader br = new BinaryReader(fs);
120 FileStream fs2 = new FileStream(txt_enc_out.Text, FileMode.Create);
121 BinaryWriter bwr = new BinaryWriter(fs2);
122 int blocksize = 4 * 1024;
123 int iteration_number;
124 if (fs.Length < blocksize)
125 iteration_number = 1;
126 else if (fs.Length % blocksize == 0)
127 iteration_number = (int)fs.Length / blocksize;
128 else
129 iteration_number = ((int)fs.Length / blocksize) + 1;
130 while (iteration_number-- > 0)
131 {
132 if (iteration_number == 0)
133 blocksize = (int)fs.Length % blocksize;
134 byte[] input = br.ReadBytes(blocksize);
135 byte[] output = new byte[input.Length];
136 for (int i = 0; i < output.Length; i++)
137 {
138 output[i] = my_Des.Encrypt(input[i]);
139 }
140 bwr.Write(output);
141 bwr.Flush();
142 }
143 bwr.Close();
144 fs2.Close();
145 br.Close();
146 fs.Close();
147 }

3.b Decryption Process
149 private void Decrypt()
150 {
151 FileStream fs = new FileStream(txt_dec_in.Text, FileMode.Open);
152 BinaryReader br = new BinaryReader(fs);
153 FileStream fs2 = new FileStream(txt_dec_out.Text, FileMode.Create);
154 BinaryWriter bwr = new BinaryWriter(fs2);
155 int blocksize = 4 * 1024;
156 int iteration_number;
157 if (fs.Length < blocksize)
158 iteration_number = 1;
159 else if (fs.Length % blocksize == 0)
160 iteration_number = (int)fs.Length / blocksize;
161 else
162 iteration_number = ((int)fs.Length / blocksize) + 1;
163 while (iteration_number-- > 0)
164 {
165 if (iteration_number == 0)
166 blocksize = (int)fs.Length % blocksize;
167 byte[] input = br.ReadBytes(blocksize);
168 byte[] output = new byte[input.Length];
169 for (int i = 0; i < output.Length; i++)
170 {
171 output[i] = my_Des.Decrypt(input[i]);
172 }
173 bwr.Write(output);
174 bwr.Flush();
175 }
176 bwr.Close();
177 fs2.Close();
178 br.Close();
179 fs.Close();
180 }

References
- Cryptography and Network Security, Fourth Edition - William Stallings, Copyright 2006.
