Introduction
As the title of this article suggests, we are going to implement the K-Means Clustering algorithm is C#. It’s been a while since I started to study this algorithm for one of my projects. It’s a nice, straightforward, yet efficient algorithm to classify some data into different groups. A couple of days ago, I decided to implement the algorithm in C# and here I want to take you all through the steps of doing so. But, first things first. Let’s take a quick look at the K-Means Clustering algorithm itself.
The K-Means Clustering Algorithm
There are a lot of pages and websites which explain the K-Means Clustering algorithm just to make you even more confused. Let’s be honest, there are also very useful and straightforward explanations out there. I try my best to show you this algorithm in the simplest way possible. As I said earlier, this algorithm is used to classify some pieces of data into different groups or, as we will call it from now on, clusters. It might have happened to you as well that at one point you needed to group similar items in a way that members of the same group have a lot in common while members of different groups vary greatly. This is what this algorithm tries to do.
To make things clearer, let’s take a look at the following pictures which I got from Wikipedia.
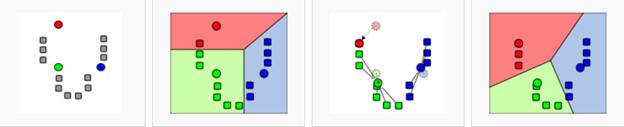
I will refer to these four pictures from left to right. So, let’s take a look at the left-hand side picture. In this picture, you see a group of gray squares which we want to cluster. You can also see three red, green and blue circles. These are called centroids. Simply put, these little guys will help us to group the gray squares. Simple enough, huh? Ok. Just stay with me.
Now, take a look at the second picture. Here, the gray squares are no longer gray. In fact, they have got the color of the circles which indicates that they are a member of that cluster. The whole area is also segmented into three smaller colored regions to show the boundaries of the three clusters. So, now we have got three clusters, all of which contain some of the squares.
The next picture shows some computation. This is the part of the algorithm in which the squares might move from a cluster to another one. But how do we decide that? I’m going to skip the answer to this question for now and get back to it later on.
Finally, the last picture shows the final result of the algorithm in which all of the squares are grouped into the three clusters. The final step of the algorithm clusters the squares in such a way that members of the same cluster have a lot in common while members of different groups are substantially different.
Now, the question that you might ask yourself is why we call it "K" and why "Means"? Well, simply put, "K" is the number of centroids that you decide to have and "Mean" is the criterion that decides which cluster a piece of data should be in. I will elaborate more on this later on. Also, please visit this page for further information on the K-Means Clustering algorithm.
The K-Means Clustering Algorithm in C#
The Data Point Data Model
Now that we know a little bit about the overall goal of the algorithm, let’s try to implement it in C#. The first thing that I have done is to create a data model to store the data I want to cluster. The data you wish to cluster could be about anything. In my case, I need to cluster some objects of a type called "Data Point". This class has two properties: Height and Weight which may correspond to the two physical attributes of a person. There is also another property called "Cluster". This property stores the cluster index which a Data Point is a member of.
public class DataPoint
{
public double Height { get; set; }
public double Weight { get; set; }
public int Cluster { get; set; }
public DataPoint(double height, double weight)
{
Height = height;
Weight = weight;
Cluster = 0;
}
public DataPoint()
{
}
public override string ToString()
{
return string.Format("{{{0},{1}}}", Height.ToString("f" + 1), Weight.ToString("f" + 1));
}
}
There is also the ToString method used to insert data points into a listbox on the main form. Here is the event handler to do this:
private void txtWeight_KeyDown(object sender, KeyEventArgs e)
{
if (e.KeyCode==Keys.Enter)
{
if (string.IsNullOrEmpty(txtHeight.Text) || string.IsNullOrEmpty(txtWeight.Text))
{
MessageBox.Show("Please enter the values for both Height and Weight.");
return;
}
DataPoint dp = new DataPoint();
dp.Height = double.Parse(txtHeight.Text);
dp.Weight = double.Parse(txtWeight.Text);
lstRawData.Items.Add(dp.ToString());
}
}
The Class Level Objects
I have also declared some objects at the class level for the main form of the application:
List<DataPoint> _rawDataToCluster = new List<DataPoint>();
List<DataPoint> _normalizedDataToCluster = new List<DataPoint>();
List<DataPoint> _clusters = new List<DataPoint>();
private int _numberOfClusters = 0;
I think the code above is clear enough, but let’s just say what the objects will be responsible for:
· _rawDataToCluster: stores the data entered by the user.· _normalizedDataToCluster: stores the normalized version of the data stored in the _rawDataToCluster. What is normalization? I will talk about it later on. · _clusters: stores the means of each cluster. Means? What is that? Don’t worry. Again, I will get back to this question. But, for the time being, I should say that the data stored in this collection decides whether a data point should move between two clusters or stay with the cluster where it already is. · _numberOfClusters: Number of clusters which we want to group the data in. In the pictures above, the number of clusters is three.
The InitilizeRawData Method
The first thing to do is to populate the _rawDataToCluster collection using the data entered by the user. I should mention that the user is supposed to enter two pieces of data into two textboxes for the Height and Weight properties. Upon pressing the Enter key, the data is added to a listbox using the following format: {32.0,230.0}.
Now, it is time to populate the _rawDataToCluster collection using the data in the listbox. Of course, there are a lot of ways to do that. I tried to stick to the most simple one:
private void InitilizeRawData()
{
if (__rawDataToCluster .Count == 0)
{
string lstRawDataItem = string.Empty;
for (int i = 0; i < lstRawData.Items.Count; i++)
{
DataPoint dp = new DataPoint();
lstRawDataItem = lstRawData.Items[i].ToString();
lstRawDataItem = lstRawDataItem.Replace("{", "");
lstRawDataItem = lstRawDataItem.Replace("}", "");
string[] data = lstRawDataItem.Split(',');
dp.Height = double.Parse(data[0]);
dp.Weight = double.Parse(data[1]);
__rawDataToCluster .Add(dp);
}
}
}
The method above simply enumerates through the items in the listbox, extracts the two pieces of data in each row using the Split method of type String, instantiates a new object of type Data Point, sets the properties and adds the object to the _rawDataToCluster.
The NormalizeData Method
The data obtained so far cannot possibly be used yet. First, we need to normalize it. Why? It’s so simple. You see, we are dealing with two different types of data: Height and Weight. They are somehow about different measurements. To give another example, if we are dealing with some data about number of days, age, number of times a customer has purchased something, etc. we need to normalize the data. We do the normalization to make sure that one piece of data (Height, for example) doesn’t overwhelm the other (Weight). Again, we may also skip the normalization step, but best practice is to do it. So, here is the code:
private void NormalizeData()
{
double heightSum = 0.0;
double weightSum = 0.0;
foreach (DataPoint dataPoint in _rawDataToCluster)
{
heightSum += dataPoint.Height;
weightSum += dataPoint.Weight;
}
double heightMean = heightSum / _rawDataToCluster.Count;
double weightMean = weightSum / _rawDataToCluster.Count;
double sumHeight = 0.0;
double sumWeight = 0.0;
foreach (DataPoint dataPoint in _rawDataToCluster)
{
sumHeight += Math.Pow(dataPoint.Height - heightMean, 2);
sumWeight += Math.Pow(dataPoint.Weight - weightMean, 2);
}
double heightSD = sumHeight / _rawDataToCluster.Count;
double weightSD = sumWeight / _rawDataToCluster.Count;
foreach (DataPoint dataPoint in _rawDataToCluster)
{
_normalizedDataToCluster.Add(new DataPoint()
{
Height = (dataPoint.Height - heightMean)/heightSD,
Weight = (dataPoint.Weight - weightMean) / weightSD
}
);
}
}
There are different methods to normalize the data we have got so far. The method used here is the Gaussian (also called normal) normalization. How does it work? Very simple. The first loop and the next two lines compute the mean of both Height and Weight for the data points. How? Just sum the values of Height and Weight up and divide by the number of items in the collection. The next step is to do something for all of the items in the collection which is subtracting both Height and Weight by the means calculated in the previous step (heightMean, weightMean) and then to the power two. The next step is to divide these two values by the number of items in the collection. Finally, the last loop populates the _normalizedDataToCluster collection by adding new objects of type DataPoint to it. The values used for the two properties are the normalized versions of the values in the _rawDataToCluster collection. Now, most normalized values will be between -3 and +3. Please, feel free to visit this page for more information about this method of normalization.
The ShowData Method
Now that we have got the normalized data, how about showing it to the user? Well, the following method just does that:
private void ShowData(List<DataPoint> data, int decimals, TextBox outPut)
{
foreach (DataPoint dp in data)
{
outPut.Text += dp.ToString() + Environment.NewLine;
}
}
This method accepts a generic list of type DataPoint, the number of floating point numbers and also a reference to a textbox where the output is to be printed. There are actually three textboxes on the form. One for showing the normalized data, one for showing the clustering history and yet another one for showing the last result of the algorithm. Again, the code is simple enough: just enumerate through all the members in the list, call the ToString method and that’s it. We get all of the items in the collection in a format like this: {Height,Weight}. Remember the ToString method?
The InitializeCentroids Method
Well, here starts the core of the K-Means Clustering algorithm. Do you remember the centroids? Those little colored circles which helped us group the gray squares. One of things about the K-Means Clustering algorithm is to set the centroids for each data item initially. How do we do this? The most basic way is to set the centroids randomly. There are also other methods which we skip for now. This is what we are going to do. So, for every DataPoint that we have got so far, we need to set the Cluster property using a random mechanism:
private void InitializeCentroids()
{
Random random = new Random(_numberOfClusters);
for (int i = 0; i < _numberOfClusters; ++i)
{
_normalizedDataToCluster[i].Cluster = _rawDataToCluster[i].Cluster = i;
}
for (int i = _numberOfClusters; i < _normalizedDataToCluster.Count; i++)
{
_normalizedDataToCluster[i].Cluster = _rawDataToCluster[i].Cluster = random.Next(0, _numberOfClusters);
}
}
One thing to bear in mind about this clustering algorithm is that a cluster must always have at least one member (here DataPoint). That’s what the first loop is about. The first loop arbitrarily adds one data point to each cluster by setting the Cluster property in both the items in _normalizedDataToCluster and _rawDataToCluster collections. Then, the second loop sets the Cluster property for the remaining data points to random numbers between zero and the number of clusters entered by the user. Why do we set the Cluster property for both the items in the _normalizedDataToCluster and _rawDataToCluster collections? That’s because at the end, we use the _rawDataToCluster to show the result of the algorithm. In other words, we use the Cluster property in the _normalizedDataToCluster to actually do the clustering and the Cluster property in the _rawDataToCluster to show the result to the user. It’s something I have decided to do. You, if you wish, can omit this part and use the _rawDataToCluster to print out the final results.
The UpdateDataPointMeans Method
Do you remember I told you that the "Means" word in the name of the algorithm is responsible to decide which cluster should hold a piece of data? If you don’t, please look back and read again. Now, the process is a little bit complex but I try to explain it in the simplest way possible. You see, we have already set the centroids of the data points. That is, we have already put the data points in some arbitrary clusters. Now, it is time to actually find the most suitable cluster for each data point. How do we decide that? Again, very simple. First, we need to calculate the mean of all of the items in a cluster (for both Height and Weight). For example, if a cluster contains three data points such as {32,65}, {16,87} and {17,60}, the mean of this cluster is 32+16+17/3 and 65+87+60/3. We store these two values in the _cluster collection. Just to remind you, the _cluster collection is generic list of type DataPoint declared at the class level. However, the Height and the Weight properties of the items in this collection no longer represent the actual values for a DataPoint, but rather the means for the corresponding properties for all of the data points in a cluster. The Cluster property for the items in this collection is a simple integer number to show the index of a cluster. However, this property for DataPoint objects in the _normalizedDataToCluster and _rawDataToCluster represent the index of the cluster that holds that DataPoint. Let’s talk about this example a little more to make things simpler. Suppose there is a DataPoint object in the _cluster collection with these properties:
DataPoint{21.6,70.6,1}
There are also three items in the _rawDataToCluster or the _normalizedDataToCluster collections with these properties:
DataPoint{32,65,1}, DataPoint{16,87,1}, DataPoint{17,60,1}
All this means that the three data points in the _rawDataToCluster collection are members of a cluster with index 1 that also has the means of the two properties of its members in its Height and Weight properties: 21.6 and 70.6.
Now, enough with these explanations, let’s look at the code:
private bool UpdateDataPointMeans()
{
if (EmptyCluster(_normalizedDataToCluster)) return false;
var groupToComputeMeans = _normalizedDataToCluster.GroupBy(s => s.Cluster).OrderBy(s => s.Key);
int clusterIndex = 0;
double height = 0.0;
double weight = 0.0;
foreach (var item in groupToComputeMeans)
{
foreach (var value in item)
{
height += value.Height;
weight += value.Weight;
}
_clusters[clusterIndex].Height = height / item.Count();
_clusters[clusterIndex].Weight = weight / item.Count();
clusterIndex++;
height = 0.0;
weight = 0.0;
}
return true;
}
This method makes use of LINQ to group the _normalizedDataToCluster based on the Cluster property. Then, it iterates through each item in each group, calculates the mean and updates the clusters collection. But, first, it makes sure that none of the clusters is empty. If even one of the clusters is empty, it returns false and doesn’t continue. This is exactly what I talked about before: At any point of time, each cluster must have at least one member.
The EmptyCluster Method
This is the method which tests the clusters to make sure each one of them has at least one member:
private bool EmptyCluster(List<DataPoint> data)
{
var emptyCluster =
data.GroupBy(s => s.Cluster).OrderBy(s => s.Key).Select(g => new {Cluster = g.Key, Count = g.Count()});
foreach (var item in emptyCluster)
{
if (item.Count == 0)
{
return true;
}
}
return false;
}
The ElucidanDistance Method
Now for the most important part of our algorithm. The idea behind the K-Means Clustering algorithm is to put similar items together, right? Correct. But what does this similarity mean? Well, it is the difference between an item and the mean of the current members of a cluster. How do you compute this difference? Well, there are a lot of ways to do this. The simplest one is the Elucidan distance method which I have used here:
private double ElucidanDistance(DataPoint dataPoint, DataPoint mean)
{
double _diffs = 0.0;
_diffs = Math.Pow(dataPoint.Height - mean.Height, 2);
_diffs += Math.Pow(dataPoint.Weight - mean.Weight, 2);
return Math.Sqrt(_diffs);
}
This method is pretty straightforward. It accepts two arguments of type DataPoint: one being the DataPoint which we want to move to a more suitable cluster and the other being the DataPoint storing the mean of the items in the target cluster. The idea behind the Elucidan method is also simple. In this case, we just need to subtract the Height and Weight of the data point in question from the means of these two properties in the target cluster, then increase value to the power two, add them up, and then return the root square of this value which is the Elucidan difference between these two data points. For more information about this method, you can refer to this page. Now that we have got the distance of a data point from the mean of the target cluster, we can decide whether to move that data point to the new cluster or not. How do we decide that? Continue reading.
The UpdataClusterMembership Method
To move a data point from a cluster to a new one, we just need to update the value stored in its Cluster property. But, the question is that how do we decide this. Well, we need to compare the Height and Weight properties of a data point with the means of these two properties in all of the clusters. Then, we need to choose the cluster with the minimum difference and move the data point to that cluster. Why? Because that cluster is the most suitable one as the difference between its mean and the data point is at the lowest level. Remember, the final goal of the algorithm is to group similar items together; items which have the least amount of difference between their values. The following code is responsible to do all this:
private bool UpdateClusterMembership()
{
bool changed = false;
double[] distances = new double[_numberOfClusters];
StringBuilder sb = new StringBuilder();
for (int i = 0; i < _normalizedDataToCluster.Count; ++i)
{
for (int k = 0; k < _numberOfClusters; ++k)
distances[k] = ElucidanDistance(_normalizedDataToCluster[i], _clusters[k]);
int newClusterId = MinIndex(distances);
if (newClusterId != _normalizedDataToCluster[i].Cluster)
{
changed = true;
_normalizedDataToCluster[i].Cluster = _rawDataToCluster[i].Cluster = newClusterId;
sb.AppendLine("Data Point >> Height: " + _rawDataToCluster[i].Height + ", Weight: " +
_rawDataToCluster[i].Weight + " moved to Cluster # " + newClusterId);
}
else
{
sb.AppendLine("No change.");
}
sb.AppendLine("------------------------------");
txtIterations.Text += sb.ToString();
}
if (changed == false)
return false;
if (EmptyCluster(_normalizedDataToCluster)) return false;
return true;
}
Let’s talk a little about this method. The outer-most loop iterates trough the items of the _normalizedDataToCluster collection. The next loop within this one calculates the Elucidan distance between each item in the _normalizedDataToCluster collection and the means of clusters stored in the _clusters collection and then stores the result of each of these comparisons in an array called distances. After that, the code calls a method named MinIndex which returns the index of the minimum value in an array. It’s very simple and I will put the code shortly. Now that we have the index of the cluster with minimum difference, we have to check whether this data point is already in that cluster. This is what the conditional part of the code does. If the data point is not already in the cluster with the minimum distance, we should move it there. How? By simply updating the value in the Cluster property of that data point. We set the changed flag to true in order to show that a change occurred in the cluster membership. Then, we also put a little bit of string in a StringBuilder object to notify the user that a data point changed cluster. If the data point is already in the cluster with the minimum amount of distance, we just print out "No Change". Simple enough? At the end of this method, we check that the changed flag is not false, we also check that none of the clusters is empty. If any of these conditions fail to meet, the method returns false. Why? Very simple. The idea behind the K-Means Clustering algorithm is that we should try to move items to more suitable clusters until no change in cluster membership happens or, as said previously, at least one of the clusters is empty.
The MinIndex Method
This method which was used in the UpdataClusterMembership method simply accepts an array and returns the index of the minimum value stored in it. It is used to find the cluster with the minimum difference for a data point to move to:
private int MinIndex(double[] distances)
{
int _indexOfMin = 0;
double _smallDist = distances[0];
for (int k = 0; k < distances.Length; ++k)
{
if (distances[k] < _smallDist)
{
_smallDist = distances[k];
_indexOfMin = k;
}
}
return _indexOfMin;
}
The Cluster Method
Here, we put the last piece of our code to cluster the data. It is a very simple method that uses most of the code we already talked about:
public void Cluster(List<DataPoint> data, int numClusters)
{
bool _changed = true;
bool _success = true;
InitializeCentroids();
int maxIteration = data.Count * 10;
int _threshold = 0;
while (_success == true && _changed == true && _threshold < maxIteration)
{
++_threshold;
_success = UpdateDataPointMeans();
_changed = UpdateClusterMembership();
}
}
This method accepts a collection of type DataPoint and a desired number of clusters. It calls the InitializeCentroids method to set some random centroids for the data points. Finally, it calls the UpdateDataPointMeans and UpdateClusterMembership methods in a loop. I have used a while loop. The three conditions to stop the loop are also important. First, the _success flag must be true; this is set by the UpdateDataPointMeans and is always true unless one of the clusters is empty. The next condition is that the _changed flag must be true; this is also set by the UpdateClusterMembership method and is always true except when one of the clusters is empty or no change happens in the cluster membership for the data points. A threshold is also set for the number of times the clustering operation is performed. This is set to ten times larger than the number of data points that need to be clustered.
Clustering and Printing the Result
The last thing to do is to use all of this and cluster some data. This is the event handler for a button which calls the Cluster method:
private void btnCluster_Click(object sender, EventArgs e)
{
InitilizeRawData();
_numberOfClusters = int.Parse(txtNumberOfClusters.Text);
for (int i = 0; i < _numberOfClusters; i++)
{
_clusters.Add(new DataPoint(){Cluster = i});
}
Cluster(_normalizedDataToCluster, _numberOfClusters);
StringBuilder sb = new StringBuilder();
var group = _rawDataToCluster.GroupBy(s => s.Cluster).OrderBy(s => s.Key);
foreach (var g in group)
{
sb.AppendLine("Cluster # " + g.Key + ":");
foreach (var value in g)
{
sb.Append(value.ToString());
sb.AppendLine();
}
sb.AppendLine("------------------------------");
}
txtOutput.Text = sb.ToString();
}
This method is very straightforward. It reads the number of clusters specified by the user and adds the right number of data points to the _clusters collection. It then calls the Cluster method passing the _normalizedDataToCluster collection and the number of clusters. After the clustering operation is done, it groups the items in the _ rawDataToCluster collection according to their Cluster property and then it prints out the members in each cluster.
Conclusion
There you have it! The K-Means Clustering algorithm in C#. This is a very beautiful and efficient clustering algorithm. I tried to explain the procedure in the simplest words possible. Hope you enjoyed it.
