Introduction
I was interested by your article, January 1, on converting a Sudoku program from VB.Net and WinForms to C# and WPF http://www.codeproject.com/Articles/855699/Complete-Sudoku-Game-in-Csharp-WPF-Silverlight as I made a somewhat similar, but perhaps more extreme, conversion a couple of years ago. Before I started I had no experience with C# or WPF – I had not even heard of them and my experience with object oriented programming extended no further than creating simple controls in Visual Basic for Excel. I hope that my experiences will persuade others that learning C# is not as daunting as it at first appears. In fact, like going for a long run, the hardest part is actually deciding to start.
Background
When I first learnt about Sudoku I thought it would be an interesting challenge to automate a solution on the computer. Since my only recent programming was using Visual Basic to write Excel macros I decided to use Excel as the front end and write all the code in VB. This worked very well but then I got too ambitious for these tools. I’d seen other Sudoku problems with different geometries, like Samurai, and I wanted to be able to handle these. This was not too difficult but I decided I needed a solver that would handle any Sudoku problem whatever the size or geometry or type of characters.
My VB code held all variables in global arrays and it became a nightmare to re-dimension these for different problems and even then it was not general enough. I needed a more powerful programming language and somehow I needed to move away from Excel as the front end as this required manually redrawing each new geometry. I decided to switch to C# for no better reason than my computer literate son in law recommended this to me as I discussed the problem with him on a ski lift in Tignes. This was a momentous event so I remember it well but I subsequently learnt that he did all his programming in C and had never actually used C# (he was going to be my mentor!). I used WPF instead of WinForms simply because I didn’t know I had a choice. Both decisions were ultimately extremely fortuitous and I continue to be impressed by the power and flexibility of this combination of tools.
Before Excel and VB I used to code in Fortran IV (mainly scientific computing in Nuclear Engineering back in the 1970s) so my prejudice was to create large shared arrays – something I found very difficult, maybe even impossible, in C#. It was only after many frustrated attempts at creating variably dimensioned global arrays that I started to understand the concept of classes and life became simpler.
Use Of Classes
I have a class called "Cell" which stores the detail of each little box in the problem, detail such as what possibilities are still available and what larger structures "Shapes" this Cell is a part of. I have a class called "Shape" which is roughly the same as the Rows, Columns and Boxes that I see in several other Sudoku programs, although somewhat more general. My definition of a Shape is any collection of one or more, not necessarily contiguous, Cells. A Sudoku Shape always has the same number of Cells equal to the number of unknowns in the problem and also has the rule that the solution in each of these Cells must be different. Different types of Shapes are used for Killer problems.
The coding for the Cell class and Shape class is included below.
public class Cell
{
private static int numSolvedCells;
string tag;
bool solved;
int solution;
int solOrder;
int nShape = 0;
int maxShape;
bool[] possibilities;
int[] shapeNums;
public void Add(string Tag)
{
this.tag = Tag;
possibilities = new bool[Characters.NumChars];
maxShape = 5;
shapeNums = new int[maxShape];
for (int nS = 0; nS < maxShape; nS++)
{
shapeNums[nS] = -1;
}
ForceUnSolve();
}
public void AddShape(int ShNum)
{
if (!shapeNums.Contains(ShNum))
{
expandIfFull();
shapeNums[nShape++] = ShNum;
}
}
public bool RemoveShape(int ShNum)
{
bool found = false;
if (shapeNums.Contains(ShNum))
{
found = true;
for (int i = 0; i < nShape; i++)
{
if (shapeNums[i] == ShNum)
{
if (i + 1 < nShape)
{
int temp = shapeNums[i + 1];
shapeNums[i + 1] = shapeNums[i];
shapeNums[i] = temp;
}
else shapeNums[i] = -1;
}
}
nShape--;
}
return found;
}
public int ForceSolve(int n)
{
int possEliminated;
if ((n < 0) | (n >= Characters.NumChars))
{
InOutUtilities iO = new InOutUtilities();
iO.Display_And_Pause(
" Invalid n in ForceSolve, n= ",
n.ToString(), " Cell = ", this.tag.ToString());
return 0;
}
if (this.solved) return 0;
possEliminated = recalculateNumPossibilities() - 1;
this.solved = true;
this.solOrder = numSolvedCells++;
this.solution = n;
for (int nCh = 0; nCh < Characters.NumChars; nCh++)
{
possibilities[nCh] = (nCh == n);
}
return possEliminated;
}
public void ForceUnSolve()
{
this.solved = false;
this.solOrder = 0;
this.solution = -1;
for (int nCh = 0; nCh < Characters.NumChars; nCh++)
{
this.possibilities[nCh] = true;
}
}
public static int NumSolvedCells
{
get { return numSolvedCells; }
}
public static void ResetNumSolvedCells()
{
numSolvedCells = 0;
}
public string Tag
{
get { return this.tag; }
}
public bool Solved
{
get { return this.solved; }
}
public int NumPossibilities
{
get
{
return recalculateNumPossibilities();
}
}
private int recalculateNumPossibilities()
{
int n = 0;
for (int nCh = 0; nCh < Characters.NumChars; nCh++)
{
if (possibilities[nCh])
{
n++;
this.solution = nCh;
}
if (n > 1) solution = -1;
}
return n;
}
public int Solution
{
get { return this.solution; }
}
public int NumShapes
{
get { return this.nShape; }
}
public int[] ShapeNums
{
get { return this.shapeNums; }
}
public int SolOrder
{
get { return this.solOrder; }
}
public bool[] Possibilities
{
get { return this.possibilities; }
}
public bool this[int Index]
{
get { return this.possibilities[Index]; }
set
{
this.possibilities[Index] = value;
}
}
private void expandIfFull()
{
if (nShape == maxShape)
{
maxShape += 5;
int[] newShapeNums = new int[maxShape];
this.shapeNums.CopyTo(newShapeNums, 0);
this.shapeNums = newShapeNums;
for (int nS = nShape; nS < maxShape; nS++)
{
shapeNums[nS] = -1;
}
}
}
}
public class Shape
{
private static int maxShapeNo = -1;
private static int numActiveShapes = 0;
private int num;
private ShapeType type;
private string label;
private int sum;
private int size;
private string[] cellTags;
private string identifier;
private int[,] partitions;
private int nPartition = 0;
private int nActivePartition;
private bool noRepeatSolns;
public int Add(ShapeType Type, string Label, int Sum, string[] CellTags)
{
this.num = ++maxShapeNo;
numActiveShapes++;
this.type = Type;
this.label = Label;
this.sum = Sum;
this.size = CellTags.Count();
this.cellTags = new string[size];
CellTags.CopyTo(cellTags, 0);
this.identifier = Shared.CreateShapeIdentifier(type, label, sum, cellTags);
switch (this.type)
{
case ShapeType.Sudoku:
case ShapeType.Killer:
noRepeatSolns = true;
break;
case ShapeType.Super:
case ShapeType.Created:
noRepeatSolns = false;
break;
}
return num;
}
public static void ResetShapeCount()
{
numActiveShapes = 0;
maxShapeNo = -1;
}
public static int MaxShapeNo
{
get { return maxShapeNo; }
}
public int Num
{
get { return this.num; }
}
public ShapeType Type
{
get { return this.type; }
}
public string Label
{
get { return this.label; }
}
public int Sum
{
get { return this.sum; }
}
public int Size
{
get { return this.size; }
}
public string Identifier
{
get { return this.identifier; }
}
public string[] CellTags
{
get { return this.cellTags; }
}
public bool NoRepeatSolns
{
get { return this.noRepeatSolns; }
set { this.noRepeatSolns = value; }
}
}
Generality Of The Code
Armed with these two classes the coding becomes very straightforward. For example, if we solve a Cell we do not have to eliminate that solution from each Row, Column and Box that contains the Cell but simply from every Shape that contains the Cell.
Having created the above classes the next step was to store them in sorted lists. This avoided the need to dimension arrays and made it simple to keep the code general. This means that exactly the same code is used to solve a samurai problem, Figure 1, as a regular 9X9 Sudoku problem, or as a 9X9X problem where numbers cannot repeat on the diagonals, Figure 2, or even as a 3 dimensional Tredoku problem, Figure 3. A little extra code was required to draw Figure 3 but no extra code was needed to draw and solve the identical problem shown as a 2 dimensional mapping in Figure 4,
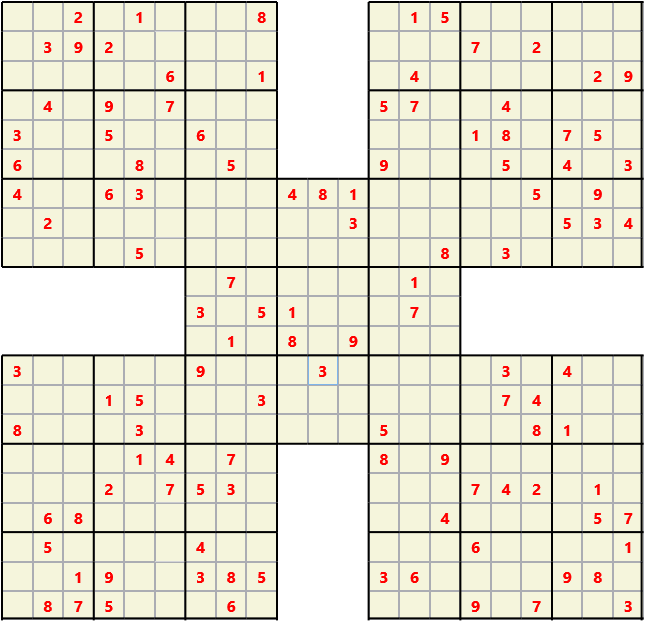
Figure 1: Samurai problem

Figure 2: 9X9X problem

Figure 3: Tredoku 3 dimensional problem

Figure 4: Solution of Figure 3 but shown as a 2 dimensional mapping, the shading is used to pick out some of the Shapes.
Note that in the 9X9X and Tredoku problems the Shapes do not all contain contiguous Cells. In fact the word contiguous has no meaning since the diagrams, above, are simply a way of mapping the problem into something we would recognise. It’s critical to the philosophy of the program that Cells are simply classes that can contain a number of possible solutions and Shapes are simply classes that reference collections of Cells. A further generalisation allows the number of unknowns to be an input parameter, this defines the sizes of the Sudoku Shapes (in normal parlance the sizes of the Rows, Columns and Boxes). Then the unknowns can be mapped to "any" symbol. I have restricted this to mean any symbol that can be represented as a single Unicode character, simply to be able to display mark-up during the solution without needing separators, Figure 5.

Figure 5. Toroidal problem with diabolical character set
The struct for the character information is shown below. This is one of the very few arrays that are used in the program.
Struct Characters
public struct Characters
{
public static int NumChars { get { return Chars.Count(); } }
public static string[] Chars { get; set; }
public static int[] Values { get; set; }
}
Algorithms
With these concepts it was relatively easy to write code that implements most of the well-known algorithms, Table 1, for solving very general Sudoku problems. It does not use the "X-Wing" algorithm because this seems to require knowledge of the geometry of the problem.
| Standard Name | My Program |
| Naked single | Single character in a Cell |
| Hidden single | Single character in a Shape |
| Naked Pair / Triple / Quad | N possibilities in N Cells |
| Hidden Pair / Triple / Quad | N possibilities in N Cells |
| Block / Column / Row | Overlapping Shapes |
| X Wing | Not implemented |
Table 1: Algorithms used in the Sudoku solver program
I give an example of the code for Naked and Hidden Pairs etc, below. This gives an example of how simple the code can be if we are not encumbered with concepts of Rows, Columns and Boxes. In fact I have 2 versions of this code, the special version, shown here, is fast but requires that at least one Cell contains an exact match. The general version allows for combinations such as (1,2), (2,3), (1,3) but is slow so is only used if all else fails.
private int nPossInNCellsInShapeSSpecial(int n, Shape s)
{
int possibilitiesEliminated = 0;
string[] cellTags = getListOfSuitableCells(n, s);
if (cellTags != null)
{
foreach (string tag in cellTags)
{
Cell c = (Cell)Collections.Cells[tag];
if (c.NumPossibilities == n)
{
List<string> selectedCells = new List<string>();
selectedCells.Add(tag);
foreach (string otherTag in cellTags)
{
if (otherTag != tag)
{
Cell otherC = (Cell)Collections.Cells[otherTag];
bool subset = true;
for (int ch = 0; ch < Characters.NumChars; ch++)
{
if (otherC[ch] && !c[ch])
{
subset = false;
break;
}
}
if (subset)
{
selectedCells.Add(otherTag);
}
}
}
if (selectedCells.Count == n)
{
possibilitiesEliminated += removePossibilitesFromRemainingCells(n, s, selectedCells);
}
}
}
}
return possibilitiesEliminated;
}
User Interface
A significant part of the programming was to develop the user interface. But most of the issues were due to my ignorance and inexperience rather than to the inherent difficulty of the task.
Choosing WPF for the user interface was originally a mistake. I wasn’t even aware that there was another possibility – Windows Forms. Every time I got stuck and needed to search for help my search would find a WinForms solution (there seems to be far more help available for WinForms than for WPF) which I would unwittingly try to implement and then wonder why it didn’t work. Eventually I twigged and now always include "wpf" in my search string. But this was not obvious at the time and may be a source of confusion to other learners. It would be helpful if there were clearer documentation about differences and why both exist and reasons for choosing each. I read somewhere that WPF is Microsoft’s preferred direction but all the help documentation seems to indicate otherwise. The actual solution grid shown in the above diagrams could not be generated in XAML since it needed to be dynamic but it is relatively easy to create an array of TextBoxes and then delete any that are not wanted. Writing the code to generate the Shape boundaries was a lot of fun, especially for Killer problems where I wanted to identify the Killer Shapes and also put the sum in the top left Cell, see Figure 6.

Figure 6: Typical Killer Problem
All the rest of the user interface, including all controls was written using XAML, and this turned out to be very easy. I like the way that, if I want to change controls around and maybe place one inside another I can simply cut and paste the XAML code.
Creating Sudoku Problems
I wanted to add the capability to create Sudoku problems and for this I am very grateful to an article published here entitled "Sudoku using Microsoft Solver Foundation" http://www.codeproject.com/Articles/419389/Sudoku-using-MS-Solver-Foundation
I use MS Solver Foundation to populate the solution grid then successively hide Cells until left with the smallest number which still gave a unique solution. This makes it easy to create new problems for any geometry.
Limitations
This was all written for PC. I have not attempted to write it for phone since I have no Silverlight knowledge. I also did not try to make this an interactive game program where the user is presented with a problem that he attempts to solve directly on the PC. Both the phone and the interactive game are currently beyond a learner’s capability so I decided to stick with a Sudoku solver and problem creator.
Conclusion And Summary
Overall this has been a great experience which has lifted my coding capability from unstructured code in Fortran IV to a semblance of competence in a modern object oriented language. I have only included a few code examples since these illustrate the power of using a language like C# and the full code is rather long and mainly involved in the user interface. I’m sure that an experienced programmer could write this much better than I can.
The points I want to stress are the general definition of Shape, which eliminates the need for separate code for Row, Column and Box, plus the use of classes for Cell and Shape which hide a lot of the complexity and enable the code to be made very general.
