Finding the solution to the game of Solitaire

• Download source code - 26.5 KB
• Download source and demo - 142 KB

Introduction

The game of Solitaire - the one where you move pins on a board - has four solutions. In order to write up a program that can systematically find one of the four, recursive programming technique can be used to iterate through possible moves - eventually finding the correct path.

Background

The game is played by one person and he has to move pins from one hole on the board to another, jumping over one pin that can subsequently be moved. The object of the game is to end up with only one pin - in the center position on the board.

The board itself is a square of 7 by 7 holes, but the 2 by 2 in each corner are not used. The game starts with 32 pins set into the holes - leaving the center hole empty.

Using the Code

The board is defined and the analysis can begin. The function Analyze can find any moves possible on the board in its current state. If there are possible move(s), pick the first one, perform it and analyze again. This is repeated until no further moves are possible. If there is more than one pin left, undo the last move and pick the next one in line.

In order to see the progress and to control the process the system uses delegates (_history and _count) to report the current status back to the WinForm.

An enumerator is used to indicate the direction of the move:

public enum Direction
{
    Up = 0,
    Down = 1,
    Left = 2,
    Right = 3
}

A given move is stored in a separate class that can both tell which pin was moved from where and to where - but also keeps track of direction and a link to the previous move as well as an indicator if this particular move has already been dealt with (see above).

public class SolitaireMove
{
    private int _id = 0; // Unique ID
    public int Id { get { return _id; } }

    private int _parent = 0; // Link to parent ID
    public int Parent { get { return _parent; } }

    private Point _from = new Point(); // The original point of the move
    public Point From { get { return _from; } }

    private Point _to = new Point(); // The point after the move
    public Point To { get { return _to; } }

    private SolitaireClass.Direction _movedirection = SolitaireClass.Direction.Up;
    public SolitaireClass.Direction MoveDirection { get { return _movedirection; } }

    private bool _used = false; // Indicate that this has already been tried
    public bool Used { get { return _used; } set { _used = value; } }

    private List<solitairemove> _moves = new List<solitairemove>();
    public List<solitairemove> Moves { get { return _moves; } set { _moves = value; } }

    public SolitaireMove()
    { }

    public SolitaireMove(int id, int par, Point fr, Point to, SolitaireClass.Direction dir)
    {
        this._id = id;
        this._parent = par;
        this._from = fr;
        this._to = to;
        this._movedirection = dir;
        this._used = false;
    }
}

The key function here can analyse the board in a given state and find possible moves (if any).

private static List<solitairemove> Analyze(int parent)
{
    List<solitairemove> temp = new List<solitairemove>();

    for (int i = 0; i <= 6; i++)
    {
        for (int j = 0; j <= 6; j++)
        {
            if (Board[i, j] == Cell.Full)
            {
                //up
                if (i >= 2)
                {
                    if ((Board[i - 1, j] == Cell.Full) && (Board[i - 2, j] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                             new Point(i, j), new Point(i - 2, j), Direction.Up));
                        movecount++;
                    }
                }

                // down
                if (i <= 4)
                {
                    if ((Board[i + 1, j] == Cell.Full) && (Board[i + 2, j] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                                 new Point(i, j), new Point(i + 2, j), Direction.Down));
                        movecount++;
                    }
                }

                //right
                if (j <= 4)
                {
                    if ((Board[i, j + 1] == Cell.Full) && (Board[i, j + 2] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                                 new Point(i, j), new Point(i, j + 2), Direction.Right));
                        movecount++;
                    }
                }
                //left
                if (j >= 2)
                {
                    if ((Board[i, j - 1] == Cell.Full) && (Board[i, j - 2] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                                 new Point(i, j), new Point(i, j - 2), Direction.Left));
                        movecount++;
                    }
                }
            }
        }
    }
 
    if (_history !=null)
        _history("To Parent " + parent.ToString() + " - added " + temp.Count.ToString() + " nodes");
    
    string s = "    ";
    foreach (SolitaireMove sm in temp)
    {
        s += sm.Id.ToString() + ": (" + sm.From.X.ToString() + "," + 
             sm.From.Y.ToString() + ") -> (" + sm.To.X.ToString() + "," + sm.To.Y.ToString() + "), ";
    }
    if (_history !=null)
        _history(s.Substring(0, s.Length - 2));

    if (_count != null)
        _count(movecount);

    return temp;
}

The function that is used recursively - i.e., call itself is listed here:

private static List<solitairemove> Analyze(int parent)
{
    List<solitairemove> temp = new List<solitairemove>();

    for (int i = 0; i <= 6; i++)
    {
        for (int j = 0; j <= 6; j++)
        {
            if (Board[i, j] == Cell.Full)
            {
                //up
                if (i >= 2)
                {
                    if ((Board[i - 1, j] == Cell.Full) && (Board[i - 2, j] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                                 new Point(i, j), new Point(i - 2, j), Direction.Up));
                        movecount++;
                    }
                }

                // down
                if (i <= 4)
                {
                    if ((Board[i + 1, j] == Cell.Full) && (Board[i + 2, j] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, 
                                 new Point(i, j), new Point(i + 2, j), Direction.Down));
                        movecount++;
                    }
                }

                //right
                if (j <= 4)
                {
                    if ((Board[i, j + 1] == Cell.Full) && (Board[i, j + 2] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, new Point(i, j), 
                                 new Point(i, j + 2), Direction.Right));
                        movecount++;
                    }

                }

                //left
                if (j >= 2)
                {
                    if ((Board[i, j - 1] == Cell.Full) && (Board[i, j - 2] == Cell.Empty))
                    {
                        temp.Add(new SolitaireMove(movecount, parent, new Point(i, j), 
                                 new Point(i, j - 2), Direction.Left));
                        movecount++;
                    }
                }
            }
        }
    }
 
    if (_history !=null)
        _history("To Parent " + parent.ToString() + " - added " + 
                 temp.Count.ToString() + " nodes");
    
    string s = "    ";
    foreach (SolitaireMove sm in temp)
    {
        s += sm.Id.ToString() + ": (" + sm.From.X.ToString() + 
             "," + sm.From.Y.ToString() + ") -> (" + sm.To.X.ToString() + 
             "," + sm.To.Y.ToString() + "), ";
    }
    if (_history !=null)
        _history(s.Substring(0, s.Length - 2));

    if (_count != null)
        _count(movecount);

    return temp;
}

and the whole process is started from here (where max indicates the maximum number of moves allowed - this is in order to control that the loop ends within a given acceptable time).

public static void Run(int max)
{
    _maxcount = max;
    SolitaireMove root = new SolitaireMove();
    root.Moves = Analyze(-1);

    Moves.AddRange(root.Moves);
    GoDeeper(root);
}

The WinForm is shown here:

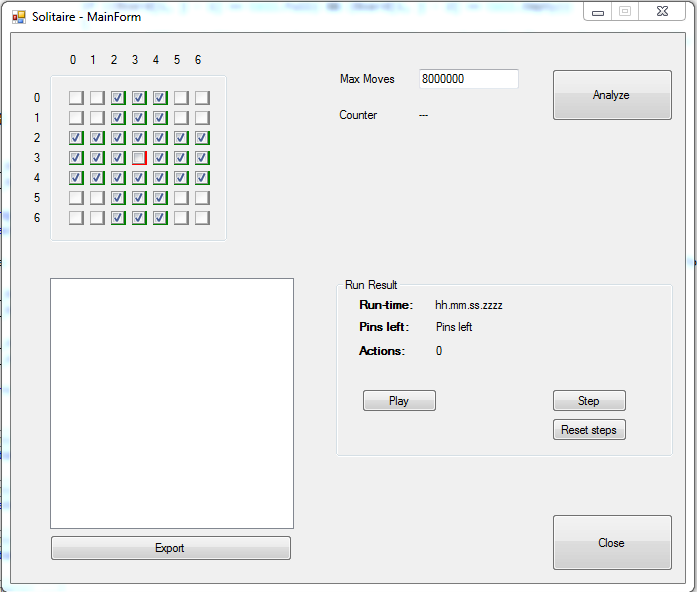
Points of Interest

By setting the max iterations to 8,000,000 the first solution is found. Due to reasons of symmetry the four solutions are actually identical.

History

This is the original version from September 2012.