Table of Contents
When it comes to optimization, majority of developers turn to parallelism but per CPU core isn't cheap. We could look to eliminate some operations to increase the per-thread performance first. That doesn't mean accuracy has to be sacrificed. With all other things being equal, the code with lesser operations shall be more performant, hence the tip title: no code is fastest code since no code needs to be executed.
We'll use the task of finding the shortest distance as an example. The formula of the length of a line is used to find the distance between 2 points, as shown below:
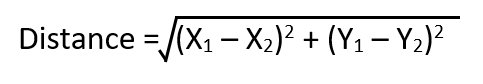
We have to compare and store the shorter distance. The interesting property of relationship of 2 numbers and their square roots is shown below: Given square root of D1 is lesser than that of D2, it should also be true that D1 is lesser than D2. We will make use of that property to forgo square root calculation.

Below is the C# code using length of line formula, meaning with Math.Sqrt() to find the nearest distance with respect to dest. The C++ code is identical, except for the sqrt() call, so it is not shown here to avoid repetition.
double shortest = 10000000.0;
int shortest_index = 0;
for (int j = 0; j < list.Count; ++j)
{
Point pt = list[j];
double x = (pt.x - dest.x);
double y = (pt.y - dest.y);
x *= x;
y *= y;
double distance = Math.Sqrt(x + y);
if (distance < shortest)
{
shortest = distance;
shortest_index = j;
}
}
This is the C# code to find the shortest distance without using Math.Sqrt() in the tight loop but Math.Sqrt() is still used to compute the distance outside the loop at the end when the shortest distance is found.
double shortest2 = 10000000.0;
int shortest_index2 = 0;
for (int j = 0; j < list.Count; ++j)
{
Point pt = list[j];
double x = (pt.x - dest.x);
double y = (pt.y - dest.y);
x *= x;
y *= y;
double distance = x + y;
if (distance < shortest2)
{
shortest2 = distance;
shortest_index2 = j;
}
}
shortest2 = Math.Sqrt(shortest2);
The benchmark is done on the computer with these specs: Intel(R) Core i7-8700 @ 3.2GHz CPU with 16GB RAM. The executable is built in Release x64 mode. Only one thread is utilized. The outer loop is done 1 million times while the inner loop is done on the List (or vector in C++) with one thousand elements.
VC++ 2019 16.4 update, /Ox
============================
With sqrt timing: 4855ms
Without sqrt timing: 1264ms
In Visual C++, we get a 74% speedup over the sqrt version. G++ and Clang++ benchmark are built and run in Windows Subsystem for Linux (Ubuntu 1804). It does seem like G++ and Clang++ has a more optimized sqrt() implementation over VC++'s. Both compilers generate faster code than VC++, despite having WSL overhead running on Windows.
Clang++ 6.0.0, -O3
============================
With sqrt timing: 1830ms
Without sqrt timing: 1047ms
With Clang++, we get 42% speedup.
G++ 7.4.0, -O3
============================
With sqrt timing: 2388ms
Without sqrt timing: 1211ms
With G++, we get almost 50% speedup, but its timing isn't as good as Clang++'s.
C# 7, .NET Framework 4.6.1
============================
With sqrt timing: 1938ms
Without sqrt timing: 1840ms
The result is surprising with C# 7. Only about 100 milliseconds shaved off the total time. So don't bother with this optimization in C# since the speed improvement is negligible (only 5% better).
- 18th January, 2020: Add bailout before squaring code suggested by scjurgen to C++ and C# benchmark
- 9th January, 2020: Initial release
