In order to draw geometrical shapes, for examples, lines, stars, circles, triangles, squares, n-gens, motiff and daisy patterns, spriographs, islamic art patterns, etc., we can use parametric forms of geometric formulae. In this text, I'll present a simple and easy way, that, with this approach, we can get symmetric or non-symmetric, regular or irregular many shapes in many types.
Introduction
Everbody knows that in digital geometry (i.e., computer graphics), we use screen coordinate system (based on Cartesian coordinate system, but vertically flipped). Yet, in the real world (i.e., mathematics, physics), this coordinate system is not enough itself to express some geometric shapes. So, we need some extra useful and facilitating coordinate systems. For examples, polar/angular, cylindrical, barycentric, logaritmic, log-polar, complex planes, and others.
In a 2D plane, we present a point P by P.X and P.Y values. Also, the same point P, we present it in polar form as P.Radius and P.Angle. From geometric aspect, P.Radius is Euclidian distance, i.e., it is the hypotenuse of right triangle sides P.X and P.Y. P.Angle is tangential ratio of P.Y/P.X.
In a similar manner, if P point is given in polar form, we get P.X and P.Y values by calculating the projection values on x- and y- coordinates. In math language, P.X = P.Radius * Cos(P.Angle) and P.Y = P.Radius * Sin(P.Angle).

The Method
The method is based on polar coordinates to calculate polygon vertex points' X and Y values. But, while drawing, it is based on screen coordinates and only use Delphi's line drawing functions, MoveTo/LineTo, nothing more.
P.S.: If we want to draw filled shapes, we can use Delphi's Polygon function instead of MoveTo/LineTo functions.
Let's explain the method by examples.
If we want to draw a simple pentagon (not filled), we first calculate the vertex points, then, connect by drawing lines between them.

Now, if we want to draw a simple star (not filled), we use same vertex points, but different order.

The main idea of this method actually is to drawing a sinusoidal wave around a circle by tracking circumference. This looks like a ripple shape.

Then, I combine the two steps above to draw the magic shapes.
The Code
Here is the magic code!
dTheta := 2*Pi / nPoints;
rotAngle := 2*Pi * rotAngle / 360.0;
for k:=0 to nPoints do
begin
theta := k * dTheta;
ripple := radius2 * Cos(nGenPer * theta);
if not SymmetricRipple then ripple := abs(ripple);
if ReverseInOut then ripple := -1.0 * ripple;
p[k].X := trunc(cX + (radius1 + ripple) * Cos(theta + rotAngle) + 0.5);
p[k].Y := trunc(cY - (radius1 + ripple) * Sin(theta + rotAngle) + 0.5);
if (k = 0) then
imgShape.Canvas.MoveTo(p[k].X, p[k].Y)
else
imgShape.Canvas.LineTo(p[k].X, p[k].Y);
end;
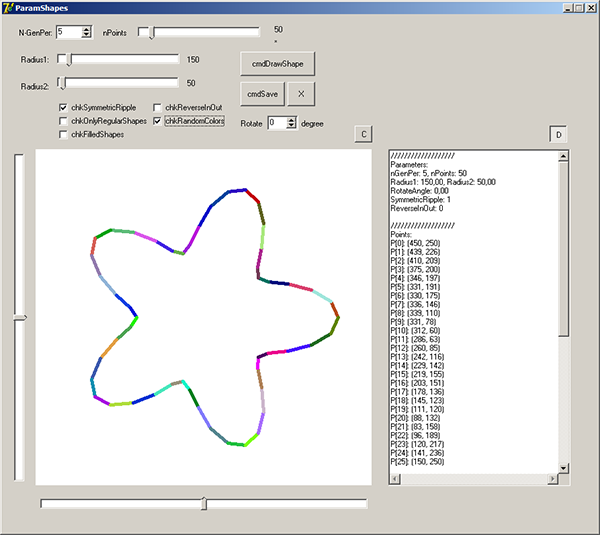
Now, let's look at the parameters that users can choose:
nGenPernPointsRadius1Radius2SymmetricRippleReverseInOutrotAngle
To understand the effects of these parameters, please try the application.
Gallery




















































Enjoy!
Conclusion
- Because of cosinus function's nature, the method behaves like modular arithmetic, and so, as a result, we get same shape by different parameters. Maybe, this superfluities and trade-off situations could be eliminated with some extra checkings.
- For quick draw, presets can be prepared. For example, if you want to draw Mitsubishi logo, just call it.
- Vertex points can be exported to vectorel formats, such as SVG or XML. Now, it saves into ordinary text files.
- Maybe sameone extends this method to 3D and we get volumetric objects easily.
References
- Wikipedia articles "Cartesian coordinate system" and "Polar Coordinate System"
- Wikipedia article "List of two-dimensional geometric shapes"
- Embarcadero topics "MoveTo/LineTo" and "Polygon"
History
- 21st April, 2020: Initial version
