Step by Step Dynamic Programing on Optimal Segment Regression Problem

• Download source - 7.4 KB

Introduction

The piecewise regression, also known as segmented regression or broken-stick regression is a method in regression analysis in which the independent variable is partitioned into intervals and as a separate line segment is fit to each interval. Piecewise regression is useful when the independent variables, clustered into different groups, exhibit different relationships between the variables in these regions or segments. The boundaries between those segments are breakpoints.

Optimal Piecewise Regression is the optima l choice of break points so that the overall fit of error is minimized. The overall fit of error is usually defined as the sum of square error between fitted data and original data.

This article use dynamic programming to find those optimal breakpoints given an array of dependent variable, x, independent variables, y, and a number of segments, k. The length of both x and y is n.

Step by Step Dynamic Programming

The key to do a dynamic programming is to define states correctly and concisely by a set of parameters.

For this particular problem, we can define a state with two parameters, i, j, cost(i, j) as the minimum error for fitting j +1 segments regressing from x[i] through x[n-1]. Please note that cost(0, k-1) is the optimal minimum cost we are looking for after solving this problem.

In order to find the optimal breakpoints, we define another state with two parameters i, j, length(i, j) as the length of first segment for fitting j+1 segments regressing from x[i] through x[n-1] with optimal minimal error. Please note length(0, k-1) is the length of the first segment for this fit. Using this length(0, k-1), we can find the first breakpoint for this optimal fit, and continue to use this length, a matrix data structure, we can continuously fine the second, the third all the way to the k th breakpoints for this optimal fit.

After defining states of a problem, the next step is to formulate a relationship between states. For this particular problem, let us assume n = 5, finding the minimum error of fitting x[0] through x[4] with 3 segments is calculated as the following:

• error[0] = cost[0,1]
• error[1] = cost[1,1] + segErr[0,0]
• error[2] = cost[2,1] + segErr[0,1]
• error[3] = cost[3,1] + segErr[0,2]

where:

• error[0] = min error of fitting 2 segments regressing from x[0] to x[4]
• error[1] = min error of fitting 2 segments regressing from x[1] to x[4] plus the error of regressing from x[0] to x[0].
• error[2] = min error of fitting 2 segments regressing from x[2] to x[4] plus the error of regressing from x[0] to x[1]
• error[3] = min error of fitting 2 segments regressing from x[3] to x[5] plus the error of regressing from x[0] to x[2]

The minimum error of fitting 3 segments from x[0] through x[5] in the minimum of error[1], error[2] and error[3].

In the above, as you can see, we define segErr[i,j] as the error of regression from x[i] to x[j], which is the sum of square error between fitted data, y_fit and original data, y from y_fit[i], y[i] to y_fit[j], y[j].

If we draw a dependent graph, we can get following. Please note I do not include segErr(i,i) in this graph simply because segErr(i, i) is always zero.

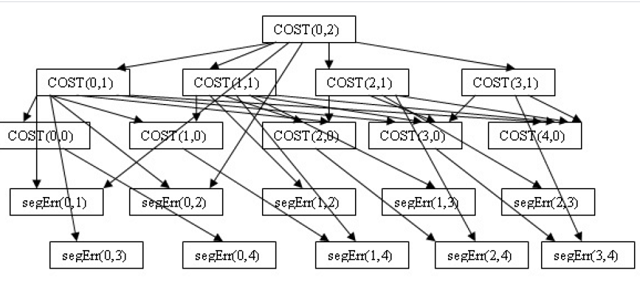
As seen above, most nodes in the above graph have been reused multiple times, so we should not use recursive solution, re computing those nodes (or sub problems) again and again, instead, we use dynamic solution to store those results somewhere, reuse the results of those nodes if needed.

There are two ways to implement dynamic programming, bottom up (or Tabulation) approach and top down approach (or memorization). From the dependent graph above, all the sub problems are needed to be solved at least once, so it is better to use bottom up approach.

The first step for bottom up approach is to fill the initial value for the states cost(i, j) and length(i, j). In order to do that, for this particular problem, we need calculate segErr(i, j) first as below:

for (int i = 0; i < len - 1; i++)
    for (int j = i + 1; j < len; j++)
        segment_error[i, j] = regression(x_value, y_value, i, j);

and then intilialize the states cost(i,0) and length(i,0):

for (int i = 0; i < len; i++){
    cost[i,0]   = segment_error[i,len-1];
    length[i, 0] = len - i;
}

The second step is to build up states cost[i, j] and length[i, j] using the dependency graph above. As shown in the graph, the j segment states are build from j-1 segment states, so outer loop should be on the segment number. The next level loop is on the index of the array of the independent variable, and dependent variable being regressed. Within this level of loop, we need compare all the choices to find the minimum error, like the example we gave above for cost[0,2].

            double temp_cost;
            for (int col = 1; col < _num_piece; col++){
                for (int row = 0; row <= len-col; row++){
                    min_cost = cost[row,col - 1];
                    min_length = 0;

                    for (int index = 1; index <= len-row-col; index++){
                        temp_cost = cost[row +index,col - 1] + 
                                    segment_error[row,row +index - 1];

                        if (temp_cost < min_cost){
                            min_cost = temp_cost;
                            min_length = index;
                        }
                    }

                    cost[row,col]   = min_cost;
                    length[row,col] = min_length;
                }
            }

The final step is usually simple, the last states is usually the optimal result. However for this particular problem, we want not only the minimal error but also we want the slopes for each segment, as well each breakpoints for this optimal fit. So we need following code as below, and output a list of data structure called piecelinear with segment length, position, and slope as its members.

public class pieceLinear{
    private double _segment_len;
    private double _error;
    private double _position;
    private double _slope;

    public pieceLinear(double sl, double err, double pos, double slope)
    {
        _segment_len = sl;
        _error = err;
        _position = pos;
        _slope = slope;
    }
}

while (position < len){
    segment_length = length[position, segment];

    if (segment_length > 0){
        error = regression
                (x_value, y_value, position, position +segment_length - 1);

        tmp = position +segment_length - 1;

        slope = (y_value[tmp] - y_value[position]) /
                (x_value[tmp] = x_value[position]);

        pl.Add(new pieceLinear(tmp-position, Math.Sqrt(error), position,slope));
    }

    position += segment_length;

    segment--;
}

Points of Interest

I found that it is quite interesting that dynamic programming can be used to data analysis problem like this one.

History

• 10^th October, 2020: Initial publication
• 11^th October, 2020: Added source code