How to Program Reversible Workflows using Finite State Machines

Introduction

The method shown here is a good way to implement complex sequences that should be reversible. It is a robust way and by following the method, it is error-proof.

Background

During my time as a programmer, I saw a lot of approaches to implement things. There is no strict way how things must be programmed, but some are easier as other ones.

The Principle

The principle of my method is shown in the next state machine. There are two types of states:

1. Stationary states (yellow)
2. Transition states (green)

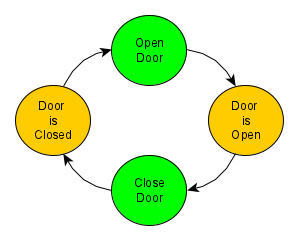
The rule is that the lower transition must be the opposite of the upper one. In this simple example "Open Door" is the opposite to "Close Door". In theory, if we do the exact opposite of something, we should restore the old situation. Therefore in the example, I have created a closed loop.

Now let's do more things, then only open the door. Let's see the sequence of going out of the house.

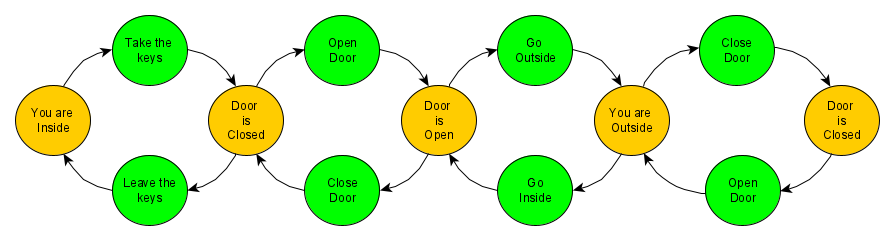
As can be seen, by reversing the individual steps, it is simple to revert the whole sequence.

To make the state machine very robust, I would suggest to implement one variable for the current state and one for the target state. The transitions can then be done from inside of the state machine by setting the target variable from outside. If the target equals the current state, then nothing is to do (ready). Let's see the first three steps from the example above.

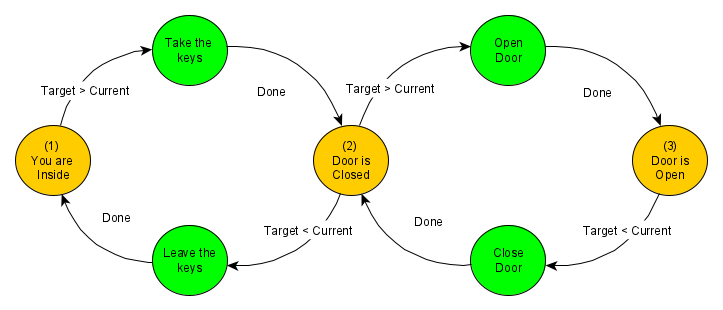
Here an Arduino sketch for that (Why Arduino? Because I have implemented a home automation for my douthers Playmobil house using Arduino today):

enum StateType 
{
  S_INSIDE = 1,
  S_INSIDE_DOOR_CLOSED,
  S_INSIDE_DOOR_OPEN,
  T_TAKE_KEYS,
  T_LEAVE_KEYS,
  T_OPEN_DOOR,
  T_CLOSE_DOOR
};

StateType _Current; 
StateType _Target; 

void setup() 
{
  _Current = S_INSIDE;
  _Target = S_INSIDE_DOOR_OPEN;
  Serial.begin(115200);
  Serial.println("Go");
}

void loop() 
{
  switch(_Current)
  {
    case S_INSIDE:
    if(_Target > _Current)
    {
      Serial.println("1->2");
      _Current = T_TAKE_KEYS;
    }
    break;
  
    case S_INSIDE_DOOR_CLOSED:
    if(_Target > _Current)
    {
      Serial.println("2->3");
      _Current = T_OPEN_DOOR;
    }
    else if(_Target < _Current)
    {
      Serial.println("2->1");
      _Current = T_LEAVE_KEYS;
    }
    break;
  
    case S_INSIDE_DOOR_OPEN:
    if(_Target < _Current)
    {
      Serial.println("3->2");
      _Current = T_CLOSE_DOOR;
    }
    //go back
    _Target = S_INSIDE;
    break;
  
    case T_TAKE_KEYS:
    _Current = S_INSIDE_DOOR_CLOSED;
    break;
  
    case T_LEAVE_KEYS:
    _Current = S_INSIDE;
    break;
  
    case T_OPEN_DOOR:
    _Current = S_INSIDE_DOOR_OPEN;
    break;
  
    case T_CLOSE_DOOR:
    _Current = S_INSIDE_DOOR_CLOSED;
    break;
  
    default:
    break;
  }
}

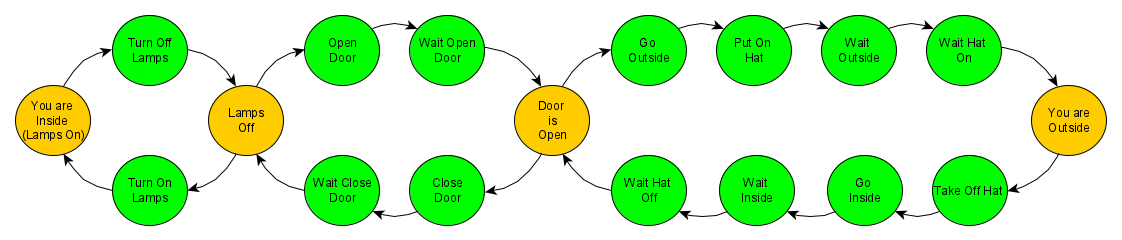
What if things must be done simultaneously? In general, I prefer to implement a wait state after a transition state. Then, it is clear that a wait time for something is required. To do things in parallel, it is possible to trigger multiple things and then add wait states for them later. The next state machine shows three situations (no wait, wait, and double wait).

Decisions can be programmed too. For example, what if there are two doors (front and back). See here:

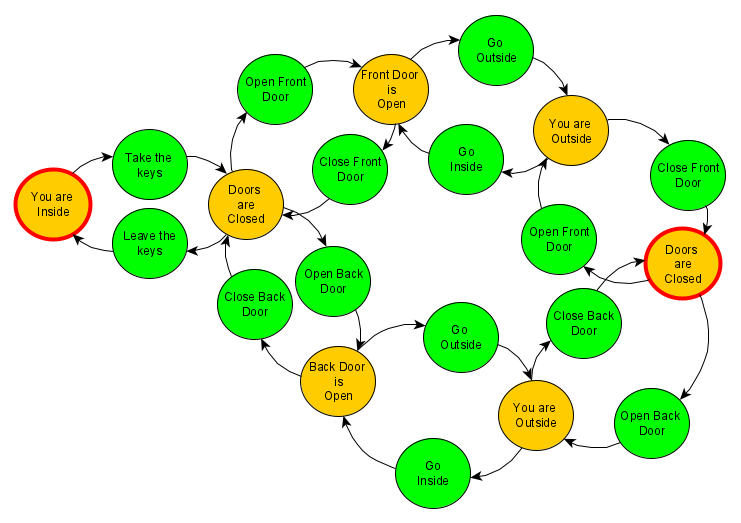
In this example, the starting point is:

1. You are inside your house.
2. The keys are on the table.
3. Both doors are closed.

The target state is:

1. You are outside.
2. You have your keys.
3. Both doors are closed.

No matter which door you choose to go outside or inside, the end result is the same.

Of course, the simple transition method with destination and current state doesn't work for this example. Some sort of pathfinding algorithm is required here.

The Rules

1. From one stationary state to another, there must be at least one transition state.
2. For every transition state, there must be the opposite one that shows back to the previous state.

In the simple Arduino code, stationary states have been marked with "S_" and transition states with "T_". That allows an easy review by checking that inside stationary states, there is no other "S_" present.

History

• 24^th January, 2021: Initial version