NoisyCrypt

• Download demo - 265.9 KB
• Download source code - 25.7 KB

Introduction

In the last decade, visual cryptography, again, has become a popular interest topic in security (encryption) and data hiding areas. For the first time, it was introduced at EUROCRYPT'94 by M.Naor and A.Shamir. It is based on sharing secrets at least by two separated/split (and also encrypted) image components. For decryption, all image components are required; elsewhere, it is not possible to get accessing the original materials. Also, the difference between normal cryptography and visual cryptography is that the stacked/blended (and also decrypted) image must be seen and approved visually by a human or humanoid.

The Method

In this tip, I'll present a simple visual cryptic method for color and black-white images using random colors (i.e., 2D noise), me named it NoisyCrypt. It's clear that there are well-known methods for implementing visual cryptography and data hiding in pictures. The most famous one is secret sharing. NoisyCrypt is conceptually based on secret sharing, but it is different as technically, very simple and also "too" funny for me. :)

As a summary, here is some well-known methods:

• Secret sharing by split components
• Using LSBs (least significant bits)
• Using selected bit plane(s)
• Bit/block shifting
• Rubic's Cube rules
• Watermarking techniques using wavelets or fractals
• Inserting into picture's non-used alpha (or auxiliary) channels
• Inserting into picture's metadata areas.

The Steps

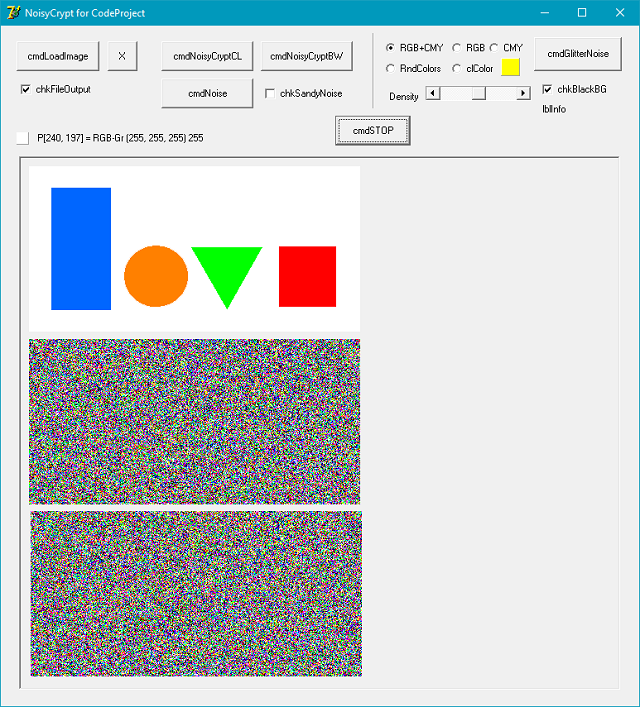
The steps are... hold a coin, toss it for heads or tails. Then, set a threshold, T, and pick a pixel from input image. If pixel value is less then T, and coin is on tail, the output pixel is the same as the picked pixel for Share 1 and inverted for Share 2, and otherwise, the output pixel is a random color. As you predict, there are four probable situations according to threshold and tossing. For color images, random color's red, green, and blue component values are thresholded to 0 or 255 before decision. While deciding for output pixel's value, it is applied for only one component but not for the other two components. That's all... Easy? Of course!

Please examine the code snippet below.

The following pictures are explaining the procedure roughly.

Input image	Noise
Share 1	Share 2
Stacked/Blended image (Color)	Stacked/Blended image (Black/White)

NOTE that the noise itself, share 1 & 2, and stacked/blended images consist of only R,G,B + C,M,Y + B,W, i.e., only 8 essential colors located at RGB cube's vertices.

To get back the original input picture from Shares 1 and Share 2 images, in Photoshop or similar apps that support layers, you must use the "Difference" or "Exclusion" blend modes for upper layer. Maybe, you can use some other blend modes, but, you'll get a nonclear image as a result.

The Code

Here is the principal code:

//
...

  H := imgInput.Height;
  W := imgInput.Width;

  nSize := abs(H * W);

  Randomize;

  T := 128; // threshold

  for y:=0 to H-1 do
  begin
    for x:=0 to W-1 do
    begin
      // c1: input color
      c1 := imgInput.Picture.Bitmap.Canvas.Pixels[x, y];
      r1 := 255 - GetRValue(c1);
      g1 := 255 - GetGValue(c1);
      b1 := 255 - GetBValue(c1);
      
      // thresholded random colors (ie 2D noise)
      r := 255 * (random(256) mod 2);
      g := 255 * (random(256) mod 2);
      b := 255 * (random(256) mod 2);

      rndNum := random(nSize);

      // sandy noise or normal noise
      if chkSandyNoise.Checked then
        flag := ( rndNum < (nSize div 2) )
      else
        flag := True;
      
      // c0: output color
      if (flag = True) then
      begin
        // tossing: heads or tails
        if (rndNum mod 2 = 0) then
        begin
          r0 := 255 - r;
          g0 := 255 - g;
          b0 := 255 - b;
        end
        else
        begin
          r0 := r;
          g0 := g;
          b0 := b;
        end;
      end;

      // ar, ag, ab for Share 1 (ie Layer A); br, bg, bb for Share 2 (ie Layer B)
      if (r1 < T) then begin ar := r0; br := 255 - r0; end else begin ar := r0; br := r0; end;
      if (g1 < T) then begin ag := g0; bg := 255 - g0; end else begin ag := g0; bg := g0; end;
      if (b1 < T) then begin ab := b0; bb := 255 - b0; end else begin ab := b0; bb := b0; end;
	  
	  // ac: output color for Share 1
      ac := RGB(ar, ag, ab); imgModified1.Canvas.Pixels[x, y] := ac;

      // bc: output color for Share 2
      bc := RGB(br, bg, bb); imgModified2.Canvas.Pixels[x, y] := bc;
    end; // x

    Application.ProcessMessages;
    if STOP then break;
  end; // y

...

Limitations and Conclusion

In this tip, I've ignored the performance issues. I mean, for simplicity, I've preferred simple and more understandable code.

On the other hand, the method demonstrated in this article doesn't care about output quality. But, it is useful for general visual cryptography on B/W and color images. Maybe, in the next post, I hope to demonstrate my own lossless, fully reversible visual cryptic method for color images.

References

1. Wikipedia, Visual cryptography
2. DataGenetics, Visual Cryptography

History

• 24^th October, 2021: Initial version