This article explains how to use sort extension for sorting two dimensional array by selected column index in selected column sort order with quick sort algorithm.
Introduction
In the realm of programming, sorting data is a fundamental task that allows for more efficient data manipulation, searching, and presentation. While sorting one-dimensional arrays is a common practice, applications often require the sorting of multi-dimensional arrays based on specific sort directives. This article introduces a C# extension class, SortExtensions, designed to extend the sorting capabilities of two-dimensional arrays using the QuickSort algorithm.
The SortExtensions class provides static methods to sort two-dimensional arrays according to given sorting directives. These directives specify the columns to sort by and the sort order (ascending or descending) for each column. This utility class can significantly enhance the way data is organized in applications dealing with complex data structures, such as spreadsheets, database records, or any application requiring multi-dimensional data sorting.
Background
QuickSort, developed by Tony Hoare in 1960, is not just a widely used algorithm in programming for its efficiency but also serves as a foundational concept in computer science education due to its elegant divide-and-conquer strategy. Its efficiency and effectiveness in handling large datasets make it a preferred choice in a myriad of applications, from system software to commercial products requiring sorted data.
The Efficiency of QuickSort
QuickSort's efficiency comes from its ability to sort "in-place" without requiring additional storage proportional to the size of the input array, making it resource-efficient. The key to its speed lies in the choice of the pivot and how effectively the array is divided into partitions. In the average case, QuickSort has a time complexity of O(n log n), making it one of the fastest sorting algorithms available.
However, its worst-case performance is O(n²), which can occur when the smallest or largest element is always chosen as the pivot. This is mitigated in practical implementations using techniques like "median-of-three" pivot selection and switching to alternative sorting methods for smaller subarrays, ensuring that the algorithm remains robust across various datasets.
Divide and Conquer Strategy
The divide-and-conquer approach employed by QuickSort is a powerful method in algorithm design, breaking a problem down into smaller sub-problems, solving each sub-problem recursively, and combining their solutions to solve the original problem. This strategy not only simplifies the sorting process but also significantly enhances performance on large arrays.
QuickSort first divides the array into two parts based on the pivot's position: elements less than the pivot and elements greater than the pivot. This partitioning ensures that, with each recursive call, the pivot element is placed in its correct position in the sorted array. The algorithm then recursively applies the same logic to the sub-arrays formed by partitioning, which gradually leads to a fully sorted array.
Using the Code
To sort a two-dimensional array, the QuickSortArray method is exposed as a public static method, which can be called on any two-dimensional array. It requires the array to be sorted and a two-dimensional integer array (sort_directive) specifying the sorting directives.
public static void QuickSortArray<T>(this T[,] array,
int[,] sort_directive)
where T : IComparable<T>
The T type parameter indicates that the method can sort arrays of any type that implements the IComparable<T> interface, making it versatile for various data types.
The actual sorting logic is encapsulated within private methods: QuickSort and Partition. The QuickSort method recursively sorts segments of the array, while the Partition method organizes the array around a pivot selected from the 'high' index according to the sorting directives.
Key Components of the QuickSort Implementation:
- Partitioning: The
Partition method determines the correct position of the pivot in the array and moves all elements smaller than the pivot to its left and larger elements to its right, according to the specified sorting directives. - Comparison and Swapping: Inside
Partition, the IsBefore method is used to compare array elements against the pivot based on the sorting directives. The SwapRows method swaps two rows in the array to reposition elements during the partitioning process.
public static class SortExtensions
{
public static void QuickSortArray<T>(this T[,] array,
int[,] sort_directive)
where T : IComparable<T>
{
QuickSort(array, sort_directive, 0, array.GetLength(0) - 1);
}
#region QuickSortArray private
private static void QuickSort<T>(T[,] array,
int[,] sort_directive,
int low,
int high)
where T : IComparable<T>
{
if (low < high)
{
int pi = Partition(array, sort_directive, low, high);
QuickSort(array, sort_directive, low, pi - 1);
QuickSort(array, sort_directive, pi + 1, high);
}
}
private static int Partition<T>(T[,] array,
int[,] sort_directive,
int low,
int high)
where T : IComparable<T>
{
T[] pivot = new T[array.GetLength(1)];
int i = 0;
for (i = 0; i < array.GetLength(1); i++)
{
pivot[i] = array[high, i];
}
i = low - 1;
for (int j = low; j < high; j++)
{
if (IsBefore(array, sort_directive, j, pivot))
{
i++;
SwapRows(array, i, j);
}
}
SwapRows(array, i + 1, high);
return i + 1;
}
private static bool IsBefore<T>(T[,] array,
int[,] sort_directive,
int row,
T[] pivot)
where T : IComparable<T>
{
for (int i = 0; i < sort_directive.GetLength(0); i++)
{
int column = sort_directive[i, 0];
int order = sort_directive[i, 1];
int comparison = array[row, column].CompareTo(pivot[column]);
if (comparison != 0)
{
if ((order == 1 && comparison > 0) ||
(order == -1 && comparison < 0))
{
return false;
}
else if ((order == -1 && comparison > 0) ||
(order == 1 && comparison < 0))
{
return true;
}
}
}
return true;
}
private static void SwapRows<T>(T[,] array, int i, int j)
{
for (int col = 0; col < array.GetLength(1); col++)
{
T temp = array[i, col];
array[i, col] = array[j, col];
array[j, col] = temp;
}
}
#endregion
}
Using SortExtensions to sort a two-dimensional array involves just a few steps:
string[,] TABLE = new string[7, 3]
{
{ "John", "Porter", "1234 Oak street, Pensacola, FL 32503" },
{ "John", "Porter", "1891 3rd Street North Westlake, OH 44145" },
{ "William", "Patterson", "4534 Virginia Street Dallas, GA 30132" },
{ "Marry", "Cortez", "7642 Fairview Avenue Milwaukee, WI 53204" },
{ "John", "Patterson", "1368 Street Road Morristown, NJ 07960" },
{ "Elizabet", "Cortez", "3698 Cedar Avenue Saratoga Springs, NY 12886" },
{ "Marry", "Mosley", "4575 11th Street Sacramento, CA 95820" }
};
- Sorting Directives: And a two-dimensional integer array for sorting directives. The first column of the sorting directives specifies the column index to sort by, and the second column specifies the sort order (1 for ascending, -1 for descending).
int[,] SORT_DIRECTIVE = new int[3, 2]
{
{0, 1},
{1, -1},
{2, 1}
};
-
And Call QuickSortArray: Use the QuickSortArray method to sort the array. Since it's an extension method, you can call it directly on the array object, passing the sorting directives as the second argument.
TABLE.QuickSortArray(SORT_DIRECTIVE);
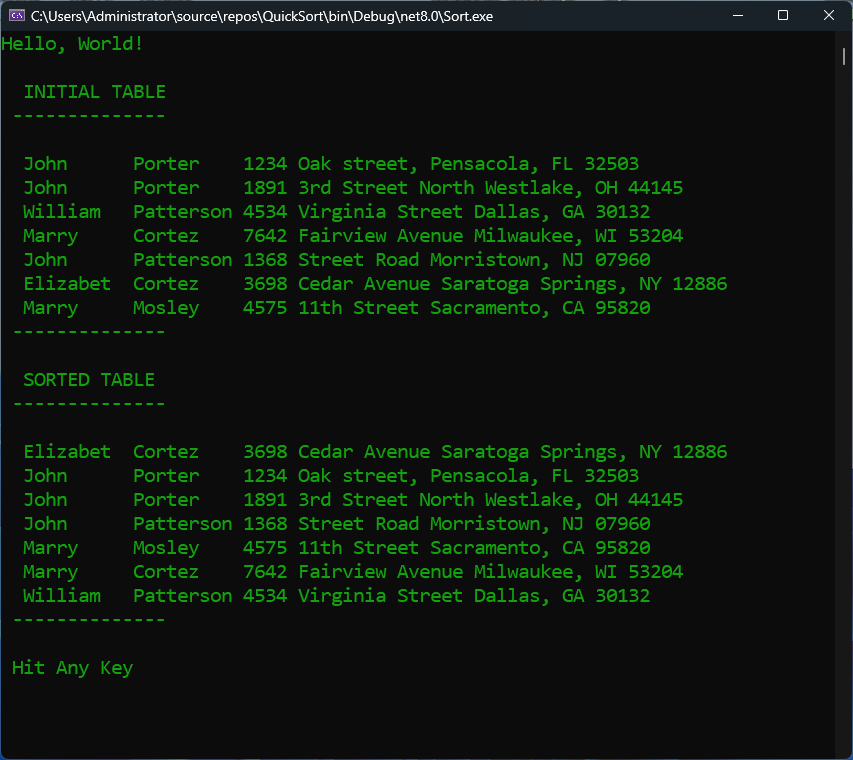
Note: The names and addresses shown in the picture are fictional.
Points of Interest
Understanding QuickSort's underlying principles, its divide-and-conquer strategy, and its practical applications underscores the importance of efficient algorithm design in software development. As developers and engineers continue to push the boundaries of data analysis and software performance, algorithms like QuickSort remain at the heart of innovation, driving the efficient processing and management of data across industries.
History
- 8th March, 2024: Initial version
