Algorithm to find all Roots of a Polynomial (of 1 variable and real coefficients) through finding the successive derivatives and employing only the Bisection method.
Introduction
Present algorithm finds Polynomials' Real and Imaginary Roots. The Polynomial may have only real coefficients, but roots may be imaginary conjugate and a root may have or not multiplicity more than one. The algorithm will find out real and imaginary roots.
Background
For example, (x^2+1)*(x-2) has two conjugate imaginary roots at -i, +i; and a real root x=2. The code will find the three roots. The code first does the multiplication
(x^2+1)*(x-2) = x^3-2*x^2+x-2
and then obtains the roots. So, you may enter the polynomial in either way x^3-2*x^2+x-2 or (x^2+1)*(x-2)
Using the code
There is one class: BisectionRootFinder. To instantiate, it is possible to pass a Math10 polynomial (Math10 is the code from my CAS calculator). More presumably, you will call shared method BisectionRootFinder.ParseFromString(strPolynomial) passing the polynomial as a string.
When instantiating, finding roots is performed.
Now, you may get the roots as an array of Double, calling rrf.GetRealRoots and rrf.GetImaginayRoots.
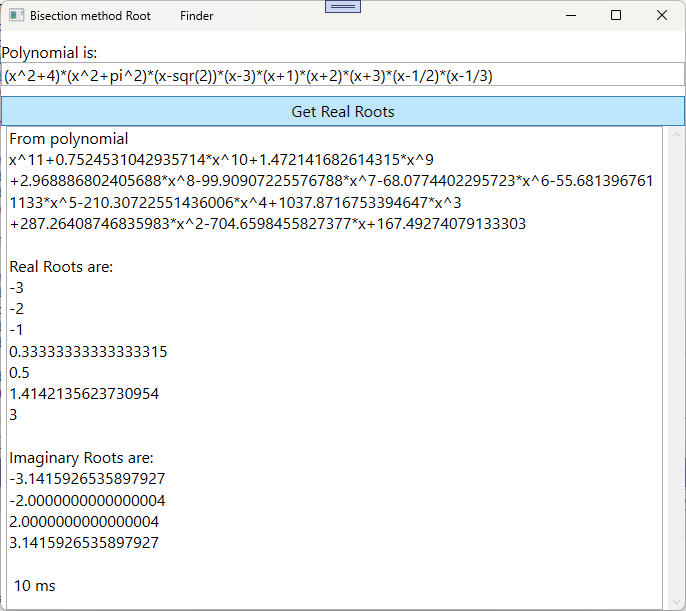
Private Sub btnRoots_Click(sender As Object, e As RoutedEventArgs) Handles btnRoots.Click
Dim sb As New System.Text.StringBuilder
Try
Globalization.CultureInfo.CurrentCulture = New Globalization.CultureInfo("en-US")
Dim ts As Int64 = Now.Ticks
Dim rrf As BisectionRootFinder = BisectionRootFinder.ParseFromString(tbPolynomial.Text)
sb.Append("From polynomial " + vbCrLf + rrf.GetInitialPolynomial.ToString + vbCrLf + vbCrLf)
sb.Append("Real Roots are:" + vbCrLf)
If rrf.GetRealRoots.Length = 0 Then
sb.Append("No real roots where found.")
Else
sb.Append(rrf.ToString)
End If
sb.Append(vbCrLf)
sb.Append("Imaginary Roots are:" + vbCrLf)
If rrf.GetImaginaryRoots.Length = 0 Then
sb.Append("No imaginary roots where found.")
Else
sb.Append(rrf.ToStringImaginaryRoots)
End If
sb.Append(vbCrLf)
Dim ts2 As New TimeSpan(Now.Ticks - ts)
sb.Append(" " + Math.Round(ts2.TotalMilliseconds).ToString + " ms")
tbRoots.Text = sb.ToString
Catch ex As Exception
tbRoots.Text = ex.Message
End Try
End Sub
Basically, if "p" is our polynomial and is of degree 4, for example, it will obtain the polynomials' successive derivatives of "p", of degree 3, 2 an 1. Then it will obtain the bounds of polynomial degree 1 (by Cauchy's bounds); next of degree 2 and 3. Through bisection method, degree 1 polynomial root (if any) is added as a new bound (interval) for degree 2 polynomial and, here on, up to polynomial of degree 4. Each new root, in polynomials of degree < 4 is evaluated in "p", to ackwnoledge if there is multiplicity. In case of multiplicity, "p" is deflated and .FindRoots is invoked recursively.
History
Version (1.0.2 2024/05/20
Naturally, the next step was to find the imaginary roots. This is done by changes of variable: y=-i*x; and z=sqr(y)
