Application's code finds the roots of a polynomial based on two points 'a' and 'b' whose real and imaginary signs are opposed. These points are obtained from or derived from the polynomial's upper Cauchy's bound.
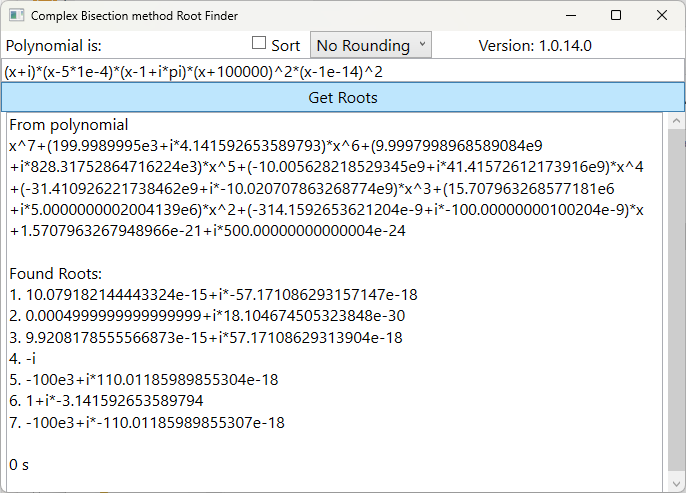
As far as I know, Bisection method has had as drawback the impracticability of knowing beforehand where p(a)*p(b) = -1. This is, where the polynomial (over real numbers) changes its' sign. In my previous article (Real Imaginary Root Finder using Bisection method), these points are found deriving the polynomial. Now, for polynomials over complex numbers, just the "upper" bound is needed.
Background
If P(x) = cnxn+an−1xn−1>+...c0, from Cauchy's radius all the roots will be inside a circle of radius
Upper radius = max { 1, ||c0/cn||, ||c1/cn||, ...,||cn-1/cn|| }. The lower radius will be the inverse, i.e.,
Lower radius = 1/(Upper radius). (If Upper < 1, then swap upper by lower).
If the radius is 1, the limits of real and imaginary parts may be ±1 and ±i.
Now, the application finds where inside these bounds two points have opposite signs in the real and imaginary parts of the polynomial value (Re(P(a))=-Re(P(b)) and Im(P(a))=-Im(P(b)) ). When these points are found, for ex. "a" and "b", it is certain that the roots will be within the set of circles of all possible pairs (a, b) centered at (a+b)/2 and radius (a-b)/2.
History
Version 1.0.4.0
Fixed some bugs.
Version 1.0.8.0
Fixed some bugs.
Version 1.0.10.0
Fixed a bug in Complex class. Powers of complex numbers elevated to non integer numbers was failing, so the last two roots, mostly, where erroneously calculated.
Version 1.0.11.0
Bisection method has been improved and so has the response.
Version 1.0.12.0 (2024/06/19)
Obtaining roots accuracy has been improved, especially when there is multiplicity.
Version 1.0.13.0 (2024/06/23)
In this release, the roots' precision is selectable and therefore the execution time.
Version 1.0.14.0 (2024/06/26)
Some variables have changed its type from Double to Rational for better accuracy.
After each successfull iteration through the circle defined by "a" and "b", the code checks for Banach's fixed point theorem conditions. If the conditions are met, Newton's method is applied .
These changes make selection of precision unnecessary, so it has been removed.
