Breaking weak RSA with C++ & GMPXX library - Part I

Introduction

Rivest-Shamir-Adleman (RSA) algorithm an asymmetric cryptography algorithm and I've provided an explanation of RSA at the following link, which is my LinkedIn profile.

"Public Key or RSA algorithm, how it is calculated and used. A simple explanation."

"C/C++ code for 4096 bit integer, RSA public key encryption using Multiple Precision Arithmetic library : GMP"

If the prime factors p and q are close, I will describe in detail in this post how to break weak RSA using only the public modulo N. Using the GMPXX (C++ GNU Multiple Precision Arithmetic) package, I have provided the C++ code. Additionally, if the difference for a given pair of numbers is huge such as |p - q|² < 2²²√N or |p - q| < 2¹¹, even if |p - q| < 2¹⁰²⁴ the code will function. And if p and q are mathematically related then it is still possible to break RSA.

Background

This article is based on a LinkedIn post by @Profssor Bill Buchanan, in which he poses the challenge, "Given only the public key (N, e), such that the prime factors p and q are close, how to decrypt the given cipher text

https://www.linkedin.com/feed/update/urn:li:activity:7202375661129216000/

I will also give two further examples in which one of the example has the modulo N is 4096 bits and is being factored as p and q with a huge difference without the encryption text.

Professor @Dan Boneh, who heads the computer security lab and leads the applied cryptography group, has an assignment problem that serves as another example.

There are two examples with the Solution 1 and the C++ code and output result. Third example is just a Solution 2 without the code and output result.

Output

Example 1

The problem statement from @Professor Bill Buchanan. Given the Public Modulo N

Quote:

N=139985042453534191530814338630181605151083085316793042716222557353976947 315273177835521525749840053133030855380542806571666507770967095566644784849 872363216671790790178991932306774136746501625197899629158716598807039762413 315491667057829160271196105730383640876012723708906672870020514209809347940669608802423

The value of prime factor p and q are as shown in the image below. Having found the private key, the decrypted message for the cipher text C is highlighted.

Quote:

C=759403557749605329827397277511270391153358711253814758994265586537563834 069578951317106641271769359009763155459549100243237444918414776051520819739 308951078932471044935528938901932839125585139958615291047606279321516578306 03055827610345212590943506302746823964240665504252713259356862520153054934758430461775

is as shown in the image below. The decrypted message is "led zepplin".

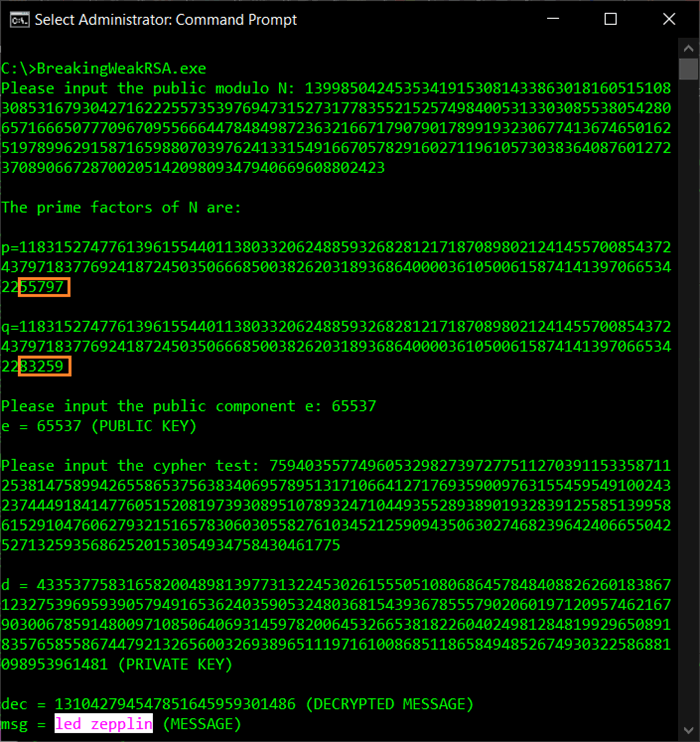
Look at the difference between p and q is marked in orange box, is very small.

Example 2

The modulo in this example is huge and it is 4096 bits modulo where [(A - √N) < 2³²] or |p - q| < 2¹⁰²⁴. Given the Public Modulo N

Quote:

N=136701171352748557830760791067094073451052752717330296857467287200427749 314688454994360294350385596122243967672715335028160598238200895345922797530 312396745491689826853365977473725783879527408074801633878039202701433848516 058779075653300544455805093591770085766567220922624447839794244041182174834 468239556270336669113098148086565069103792403512719311465515121288449125459 571651433490921460112580652868108100301221860197231066864120475986292904735 279305068898762832182264929029689869871909358261877551847323992509552576244 184871370554211041507630648451495598193666647444177437656319076781277943805 078597732600807500600893552081283155774820550135171212021686309341249855432 864490067347685237436212916753489269022611304526341310619253728832585519231 291972763114367440503019507423972430439294427235477110880889644167852035630 823920209429788013804119315895906963850736459907145365807106222701707550220 744229452130569352399727351142786657144424992223335899295744976046212307204 299032048140436036417832629288639445270301178913821429373055988904096433718 415454333119110661673671969783466126593115213492392854396433838395287150461 016374371342854881582427787463795478474958675936693110335523210170294494217 747530167920687561509467853544120731

The value of prime factor p and q are as shown in the following output. It took around 1 hour in my machine. Please also look at the difference in the prime p and q marked in an orange box. Number of iterations is 1483934994. Whereas in the above solution the number of iterations is just <2. It means RSA with 2048 bits modulo N can be easily broken.

Using the code in C++

This code works for both the above examples and is self-explanatory.

#define NOMINMAX 

#include <stdio.h>

#include <iostream>
using namespace std;

#include "gmp.h"
#include "gmpxx.h"
#pragma comment(lib, "mpir.lib")
#pragma comment(lib, "mpirxx.lib")

// Conver the hexa decimal string to ASCII string
string HexToStr(string szHex)
{
    string szMsg;
    for (int i = 0; i < szHex.length(); i += 2)
    {
        string szSub = szHex.substr(i, 2);
        //char ch = stoul(szSub, nullptr, 16);
        char ch = stoul(szSub, nullptr, 16);
        szMsg += ch;
    }
    return szMsg;
}
void wmain()
{
    mpz_class N("0");

    cout << "Please input the public modulo N: ";
    string szN;
    cin >> szN;
    N = szN;

    // Since there is no ceiling function in GMP so we increment by 1
    // and perform sqrt and then decrement by 1 to get ceiling effect.
    mpz_class A = N + 1; 
    mpz_sqrt(A.get_mpz_t(), A.get_mpz_t());
    A -= 1;

    // We iterate till 2^128 and to find A(i) using √N
    mpz_class pow;
    mpz_ui_pow_ui(pow.get_mpz_t(), 2, 128); // 2^128

    mpz_class p, q;
    // Iterate A(i) by one and fine x(i)
    for (mpz_class i = 0; i < pow; i++)
    {
        mpz_class AS = A * A;
        mpz_class XS = AS - N;
        // We perform absolute is in case XS is negative.
        mpz_abs(XS.get_mpz_t(), XS.get_mpz_t());
        // Find x
        mpz_class X;
        mpz_sqrt(X.get_mpz_t(), XS.get_mpz_t());
        // Find p(i) and q(i)
        p = A - X;
        q = A + X;
        // Multiply p(i) and q(i) and compare with the original modulo N
        // If both are same then p(i) and q(i) are the prime factors of N
        // and stop iterating.
        mpz_class NN = p * q;
        if (N == NN)
        {
            cout << endl << "The prime factors of N are:" << endl << endl;
            cout << "p=" << p.get_str() << endl << endl;
            cout << "q=" << q.get_str() << endl << endl;
            //cout << "N=" << NN.get_str() << endl;
            break;
        }
        A++;
    }
    mpz_class e(0);
    cout << "Please input the public component e: ";
    string sze;
    cin >> sze;
    e = sze;
    if (e != 0)
    {
        cout << "e = " << e.get_str() << " (PUBLIC KEY)" << endl << endl;

        mpz_class enc(0);
        cout << "Please input the cypher test: ";
        string szenc;
        cin >> szenc;
        enc = szenc;

        // Calculate the totient of N
        mpz_class phi;
        phi = (p - 1) * (q - 1);

        // Calculate the private key d. d and n together form the private key.
        // d = (e ^ -1) mod phi. d is the inverse of e mod phi.
        mpz_class d;
        // This was giving wrong result. It worked for small number.
        //mpz_powm_ui(d, e, -1, phi);
        // So I used mpz_invert to find the inverse of e.
        mpz_invert(d.get_mpz_t(), e.get_mpz_t(), phi.get_mpz_t());
        cout << endl << "d = " << d.get_str() << " (PRIVATE KEY)" << endl << endl;

        // Decrypte the encrypted message enc using the PRIVATE KEY d such that
        // dec = (enc ^ d) mod n
        mpz_class dec;
        mpz_powm(dec.get_mpz_t(), enc.get_mpz_t(), d.get_mpz_t(), N.get_mpz_t());
        cout << "dec = " << dec.get_str() << " (DECRYPTED MESSAGE)" << endl;

        string szMsg = "";
        szMsg = HexToStr(dec.get_str(16));
        cout << "msg = " << szMsg.c_str() << " (MESSAGE)" << endl;
    }
}

How It Works

Solution 1

Suppose we have two points p and q so,

N = p X q, and 

A is the midpoint of p and q. The relationship between p, q, A and N can be shown in the image as follows.

The only value from the above figure that is known is N; the other values are unknown. x is distance between, p and A, and, q and A, respectively. Always remember that √N < A. I have given explanation below for beginners. Our aim is to find the prime factors of N, p and q. We can find the prime factor by iterating √N towards either p or q but this is not a workable option. However, there is usually a better way to do. From the previous image, we also know that N = p X q.

since A is the midpoint between p and q, therefore p = (A - x) & q = (A + x),

Since N = p X q, substituting p and q from the above equation we get,

N = (A - x) X (A + x) = (A² - x²). So, N = A² - x². Therefore,

Finding 'A' by Iteration

Since N is known we need to find A. We will find A using √N. We will iterate √N towards A such that,

A₀=ceiling(√N) <- By ceiling we ignore the fractional part.

A₁=A₀+1 <- Increment by one for every iteration

.......

A_(i-1)=A_(i-2)+1

A_i=A_(i-1)+1.

For every value of A_i we will substitute for A in the above equation and find x_i (i.e. x). 

We have A_i and x_i, we get,

p_i=(A_i-x_i) and q_i=(A_i+x_i)

If N = (p_i X q_i) then p_i and q_i are the prime factors of N.

p=p_i and q=q_i

Solution 2

Following is the problem posted by Professor Dan Boneh. Given modulus N which is a product of two close primes p and q. Find the two factors. Hint:

Let p' = 3p and q' = 2q and N' = p' X q' = 3p X 2q = 6N.

Given p', q' and N' we can use the same technique described in Solution 1 as shown in the figure below.

However, the dilemma mentioned above has a twist. p and q are odd numbers since they are prime. That is, 2q is even and 3p is odd and moreover, 3p+2q is odd. As a result, the midpoint A is a fraction rather than an integer, and its fractional value is always .5. Since Solution 1 iterates by 1, Solution 1 cannot solve the aforementioned problem. Solution 1 will work for this case, and you can factor the modulo with ease if we iterate by .5 instead of 1. If you would rather not work with fractions, you can multiply every point in the line above by 2, including A. This will make A's midpoint an integer, as seen in the picture below.

However, Solution 2 will still not allow the C++ code to function. It won't function unless you make a few changes to the code which I have not provided.

For Beginners

If you still have difficulty in understanding the above problems, please read this.

Given two points a and b

Let N = a X b. If a = b then

N = a X a or b X b = a² or b²

The average A is,

Therefore,

If the distance between a and b is growing, then

Conclusion

Most professional programmers could, given sufficient time/motivation, implement an elliptical crypto application that would be able to encrypt and decrypt data. However, such an application would inevitably be vulnerable to a number of side-channel attacks, and as such would not actually be secure. Implementing crypto isn't inherently that difficult, but securely implementing crypto is, and so is discouraged for the same reason as inventing your own cryptosystem. This is Part I, means there is another attack called Wiener's attack which I will be posting it later.