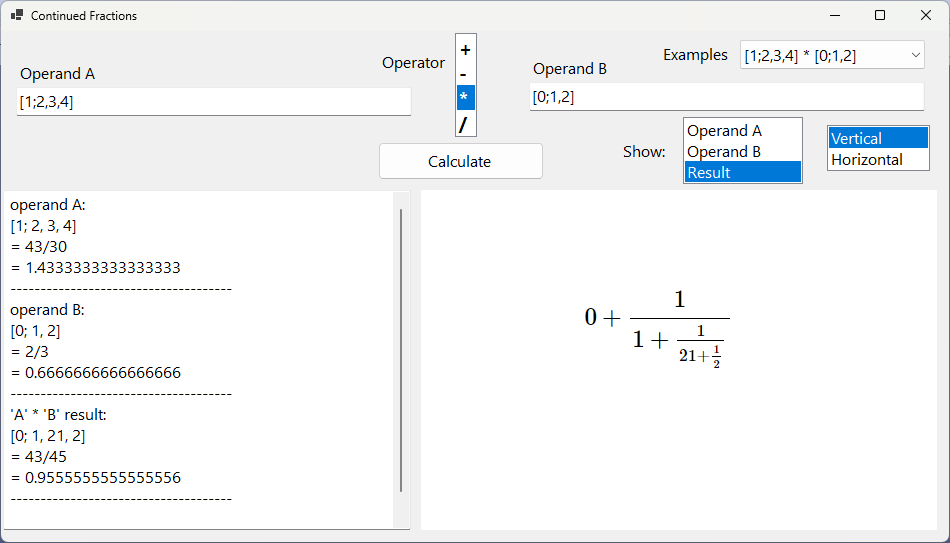
The calculator does basic operations (-, +, *, /) of two finite simple continued fractions operands and shows the result, or the operands, in a browser control (with MathJax).
Introduction
I am new to simple continued fractions (SCF) but there is a lot of literature about them out there
and, as it seems, many mathematical applications, including fractals.
Background
CF class is the only class to do the four basic operations (-, +, *, /). I have followed two documents from S. Mugassabi [1] [2] to perform them.
Using the code
Instantiation can be done in three ways, depending on the arguments passed:
- a numerator and a denominator
- a double
- a List(Of BigInteger) object
Passing a Double, it is converted into a numerator and a denominator equal to one. If the double value is not integer, it is multiplied by 10 (as well as the denominator) as much as needed until it is converted into an integer. This is because the terms are stored as Biginteger and if not the decimal places would be lost. For example, if we instantiate:
Dim operandA as new CF(1.5)
1.5 is converted to a numerator (=15) and a denominator (=10) and simplified to 3/2 (=1+1/2). The integer part is one and the fraction is 1/2. So, it will define two terms [1; 2] = 1+1/2
Passing a list of BigInteger is the equivalent to define the SCF. For example, if the list is {1,2,3} the SCF will look like:
1
1 + --------------
1
2 + -----
3
To operate just do the math as with numbers:
Dim operatorA = new CF(1.5)
Dim operatorB = new CF(0.5)
Dim operatorC = operatorA + operatorB
Console.WriteLine(operatorC.ToString)
Limitations
The calculator can operate small or big Double values, for example 1e-100 or 1e+100, but the ToDouble() method will be limited, of course, to Double maximum and minimum.
This is not the case of method ToNumDen() that returns a BigInteger array of two elements: the calculated numerator and denominator of all the SCF.
History
Version 1.0.3 (2024/07/12)
Some fixes, including the CF class was sometimes generating a single term.
Version 1.0.5 (2024/07/21)
There was a fix in the particular case of addition and subtraction where the result had two terms. For example, 1/3+1/6.
Released a Console (Cli) version.
Version 1.0.6.0 (2024/07/24)
There was a fix in some particular cases of multiplication and division where the shorter operand had less than three terms.
Showing periodic continued fractions has been improved.
References
[1]. Mugassabi, S. I., & Mistiri, F. (2015). “The Elementary Arithmetic Operators of Continued Fraction”.
[2]. Mugassabi, S. I., & Amsheri, S., M. (2019). “The Multiplication and Division of Simple Continued Fractions”.
