Introduction
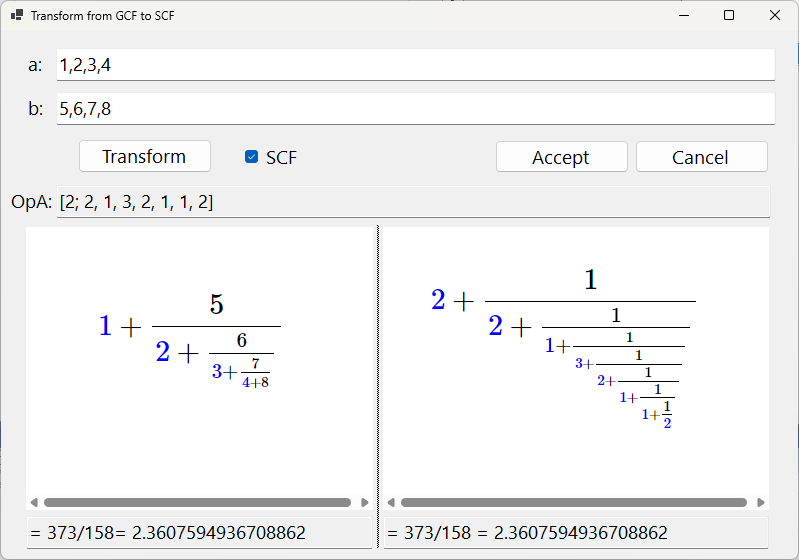
Generalized continued fractions are transformed into simple continued fractions (SCF) and
basic operations (-, +, *, /) can be done.
So it is possible to operate (-, +, *, /) SCF or and also, if you allow me to, "simple rational continued fractions" (SRCF). SRCF will have all numerators equal to one but the terms may be rational, like in the image:

Background
CF class does the four basic operations (-, +, *, /) where the operands may be SCF or SRCF.
Transform_GCF_2_SRCF class transforms GCF to SCF or SRCF that, later, can be operated.
Using the code
Instantiation can be done in five ways, depending on the arguments:
- a numerator and a denominator
- a Rational;
- a double
- a List(Of Rational) object
- a List(Of Rational) object and the term index where starts the terms periodicity. No
periodicity is indicated by passing index = -1. If there is periodicity some extra terms are
added.
Passing a Double, it is converted into a numerator and denominator equal to one. If the double is not integer, it is multiplied by ten (as well as the denominator) as much as needed until it is an integer.
To operate just do the math as with numbers:
Dim operandA = New CF(1.5)
Dim operandB = New CF(0.5)
Dim result = operandA + operandB
Trace.WriteLine(result.ToString())
Dim A() As Rational = {New Rational(2.0), New Rational(2.0, 3.0)}
Dim B() As Rational = {New Rational(-1.0), Rational.ParseFraction("-2 / 3")}
Dim lstA As New List(Of Rational)
lstA.AddRange(A)
Dim lstB As New List(Of Rational)
lstB.AddRange(B)
Dim opA As New CF(lstA)
Dim opB As New CF(lstB)
result = opA + opB
Trace.WriteLine(result.ToString())
Limitations
The calculator can operate small or big Double values, for example 1e-100 minus 1e+100, but the ToDouble() method will be limited, of course, to Double maximum and minimum.
This is not the case of method ToNumDen() that returns a Rational having BigIntegers in the numerator and the denominator.
Conclusion and Points of Interest
I have found interesting that CF of π:

converted to SRCF seems to also follow a pattern:

History
Version 1.0.3.0 (2024/07/09)
Some fixes have been taken.
A new feature when transforming CF window, allows to include formulas. In this manner, for example:
4,(k*2-1)^2 will generate terms
4,(1*2-1)^2,(2*2-1)^2,...
2,1 will generate terms
2,1,1,...
the last term -if Not otherwise indicated- will repeat
as many times as we later indicate
Version 1.0.4.0 (2024/07/10)
- Some improvements have been made, especially in the formula code.
- BigIntegers now display all their digits.
Version 1.0.5.0 (2024/07/11)
- Fixed a bug on recursion causing stack overflow.
- Updated Math10's Rational class so fractional outputs are displayed as fractions instead of decimals.
Version 1.0.6.0 (2024/07/12)
Some fixes, including the CF class was sometimes generating a single term.
Version 1.0.7.0 (2024/07/21)
There was a fix in the particular case of addition and subtraction where the result had two terms. For example, 1/3+1/6.
Version 1.0.8.0 (2024/07/24)
There was a fix in some particular cases of multiplication and division where the shorter operand had less than three terms.
Showing periodic continued fractions has been improved.
Version 1.0.9.0 (2024/07/27)
Still, there was a bug when showing periodic continued fractions.
References
[1]. Mugassabi, S. I., & Mistiri, F. (2015). “The Elementary Arithmetic Operators of Continued Fraction”.
[2]. Mugassabi, S. I., & Amsheri, S., M. (2019). “The Multiplication and Division of Simple Continued Fractions”.
[3]. https://r-knott.surrey.ac.uk/Fibonacci/cfINTRO.html#section11.1
[4]. https://en.wikipedia.org/wiki/Generalized_continued_fraction
[5]. https://poset.jp/posts/continued-fractions-attempt-1/continued-fractions-part-2/
[6]. A remarkable Continued Fraction for pi - Mathematics Stack Exchange
