CalcStar: A C++ Math Expression Evaluator

The following is an example implementation using the GT Graphical User Interface system.

Download source

Download GtCalculatorApp_20170114.zip

Version 1.1.0
Date: 12/01/2016
Author: Anthony Daniels
email:  AnthonyDaniels99@gmail.com

Introduction

CalcStar is an expandable, fast C++ function evaluator that gives the user the same computational power as a scientific calculator. The library can be used to provide function evaluation capability in any C++ project. The function evaluator tokenizes any input function and compiles it into an RPN stack before evaluating it providing the user an answer. Functions are typed in a C++ syntax format and in in-fix notation (i.e 2 + 2). CalcStar supports the use of variables in the functions. Using CalcStar starts with including the library header.

#include <CalcStar.h>

From there, the user declares a function evaluator, sets the expression to be evaluated and variables, then evaluates the function giving an answer. Once an equation has been compiled, the user can evaluate with the existing RPN stack to avoid the extra computational effort of compiling every execution. However, it should be noted that compiling is very fast. Below is an example usage of the function evaluator that can be found in the supplied TestApp.

Std::string strFunc;
strFunc = "(2 + 2)/3 * pow(3,2) - 2";
this->m_objFuncEvaluator.Set_strExpression(strFunc);
m_objFuncEvaluator.Evaluate();
dblAnswer = m_objFuncEvaluator.Get_dblCurrValue();

Setting variables is as simple as:

CSVariable objVarTemp;
objVarTemp.m_strVarName = "X1";
objVarTemp.m_dblCurrVal = varValue;
m_objFuncEvaluator.AddVariable(objVarTemp);

Updating the value of a variable is simple as well.

m_objFuncEvaluator.UpdateVariable(strVarName,dblNewVal);

CalcStar Design

CalcStar is a general purpose calculator. Essentially, it is on par with any infix notation scientific calculator (think TI-83). When the CalcStar calculates the answer to an expression, it goes through three phases: Tokenization, Compilation, and Execution. In Tokenization, the string mathematical expression is parsed into a collection of "tokens" or mathematical words. The token is the basic unit of operation in a mathematical expression. Below is the list of token types in CalcStar:

enum CSTAR_DLLAPI CSTokenType
 { //IMPORTANT NOTE!!! these operators are in order of operation prescedence
  //THE HIGHER THE NUMBER THE HIGHER THE PRESCEDENCE
  //DO NOT CHANGE THIS ORDERING, HARDCODING IS USED BASED ON ENUMERATED TYPES
  //
  NOOP = -1,
  OPENPAREN = 0,
  OPENBRACKET,
  OPENBLOCK,
  CLOSEPAREN,
  CLOSEBRACKET,
  CLOSEBLOCK,
  COMMA,
  LT,
  GT,
  LTE,
  GTE,
  NEQ,
  EQ,
  AND,
  OR,
  NOT,
  SUB,
  ADD,
  DIV,
  MULT,
  POW,
  NEG,
  ASSIGN,
  NUMBER,
  VAR,
  FUNC
 };

Function is used for any type of user defined function, such as pow() for power. Functions have a "signature" followed by an "(". It should be noted that if CalcStar can’t find the function signature in its registry, it will consider that token a variable. The CSToken object has the following member variables:

//This is a thin class, so member
variables are public
//like in a typical struct
//!The token type of this RPN Unit
CSTokenType m_objTokenType;
 
//!The string representation of the token, also the signature
std::string m_strToken;
 
//!Token's associativity
CSAssociativity m_objAssociativity;
 
//!Numeric version of token if applicable
double m_dblToken;

Once the expression has been tokenized, that stack is compiled into a Reverse Polarity Notation (RPN) stack to allow for computation. It creates the RPN stack by using a modified version of the Shunting Yard Algorithm, a well known algorithm in computer science. RPN stacks preserve order of operations and allows the computer to simply scan through the stack once performing the operations along the way. As operations are performed, their inputs and the operator are replaced with a single CSRpnUnit that is the output number for that portion of the calculation. The process continues until a single output number is left. This is the answer of the expression.

CalcStar Expressions

The user may write any infix notation C++ style mathematical expression that evaluates to a single number. An example of this is: ( 2 + 3) * X – 1, where X is a variable equal to 3.1415926. The built in operators and functions of CalcStar are as follows:

Basic Functions

Name	Signature	Name	Signature
Add	+	Boolean And	&&
Subtract	-	Boolean Equal	==
Multiply	*	Boolean Not	!
Divide	/	Boolean Not Equal	!=
Exponential	exp	Boolean Or	||
Power	pow	Greater Than	>
Natural Log	ln	Greater Than or Equal	>=
Log2	log2	Less Than	<
Log10	log10	Less Than or Equal	<=
Absolute Value	abs	Ceiling	ceil
Square Root	sqrt	Floor	floor
	Truncate	trunc

Trigonometric Functions

Name	Signature	Name	Signature
Sine	sin	Arc Sine	asin
Cosine	cos	Arc Cosine	acos
Tangent	tan	Arc Tangent	atan
Hyp Sine	sinh	Arc Hyp Sine	asinh
Hyp Cosine	cosh	Arc Hyp Cosine	acosh
Hyp Tangent	tanh	Arc Hyp Tangent	atanh

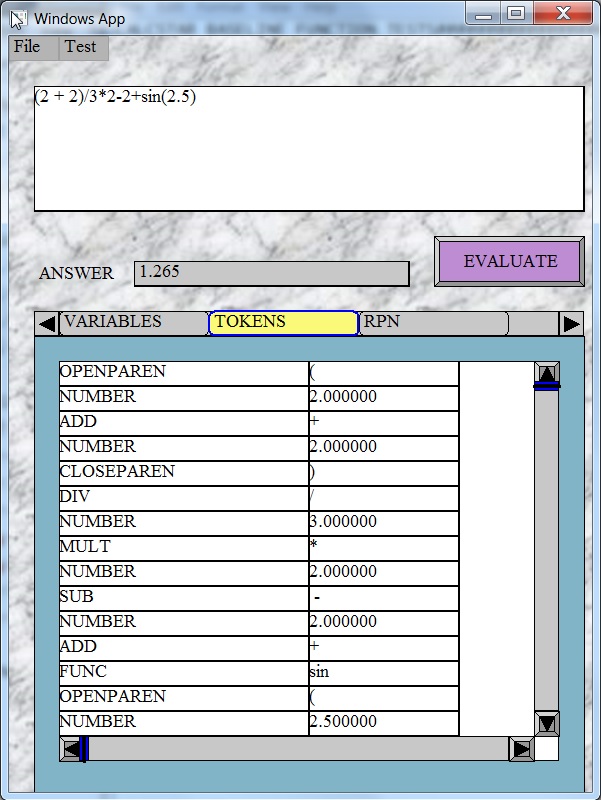
The following is a screen shot from the GT based Calculator application.  For more information on GT please see this article.

https://www.codeproject.com/tips/897483/gt-a-cplusplus-graphical-user-interface-library-and-system

The Test Menu runs the Prashtow test series from ExprTK.  It has approximately 6600 tests and the answers were generated in the Excel file in the Calculator\TestSuite folder.  The results are shown in the "TestCalcStar_Results.txt" file that is generated.  Currently out of the 6600 tests CalcStar is only failing 20 tests.  Most of these failures revolve around precision issues of large numbers coming out of the CSV generated answers file.  The others revolve around the log function.  This is being investigated.

 

Expanding CalcStar

One of the most important features of CalcStar is the ease with which it can be expanded. The user can add new functions to the system with minimal effort using the existing set of operators and functions as an example. Every CSRpnUnit has a pointer to an CSOpBase object that is responsible for performing the actual calculation when Evaluate() is called. CSOpBase is the base class for all operations and functions in CalcStar. It is essentially a functor design, with a virtual function:

virtual int OpEval(std::vector<CSRpnUnit> &
arrObjCalcStack, bool & blnCalcSuccessful,int intCurrPos) = 0; 

This function gets overridden whenever the user inherits from CSOpBase. To illustrate this, let’s look at the CSOpPower function in detail.

class CSOpPower: public CSOpBase
{
public:
//!Default Constructor
CSOpPower();
//!Default Destructor
~CSOpPower();
 
//!Perform the operation on the stack
virtual int OpEval(std::vector<CSRpnUnit> & arrObjCalcStack,
bool & blnCalcSuccessful,int intCurrPos);
 
};
 
//OBJECT FACTORY REGISTRATION CODE
static bool blnCSOpPower_Registered = 
CSTAR::GetOpBaseFactoryPtr()->Register<CSOpPower>("pow");

CSOpPower inherits from CSOpBase and implements the virtual OpEval function to perform the actual power calculation. Outside and after the class definition, the new function is registered with the OpBase Factory by the GetOpBaseFactoryPtr()… line of code. The template argument is the class being registered. The string supplied to the function is the signature of the function. Registering is all the user has to do to install new functions to be used. When the library compiles, it registers all of the functions this way. In the implementation of the OpEval:

//!Perform the operation on the stack
int CSOpPower::OpEval(std::vector<CSRpnUnit> & arrObjCalcStack,
bool & blnCalcSuccessful,int intCurrPos)
{
   //FUNCTION: pow(Number, numdecimal)
   //first determine if the necessary inputs are valid, if they are,
   //then get the input numbers and perform the calculation,
   // Once the calculation is made
   // then replace the operation and input tokens
   // with the output number token
 
   char chrOutput[256];
   for (int i = 0; i < 256; chrOutput[i++] = '\0');
   blnCalcSuccessful = true;
   bool blnValid;
   double dblOutput;
   CSRpnUnit
   objOutput;
 
   try{
      this->ValidOpInputs(arrObjCalcStack,blnValid,intCurrPos,2);
 
      if(blnValid)
      {
          //then valid inputs, perform the power calculation
          //then replace the sin calculation results with the single number
          double dblNum, dblPower;
          this->GetOpNumber(&(arrObjCalcStack.at(intCurrPos - 1)),dblPower);
          this->GetOpNumber(&(arrObjCalcStack.at(intCurrPos - 2)),dblNum);
 
          dblOutput = pow(dblNum,dblPower);
 
          objOutput.m_objTokenType = NUMBER;
          objOutput.m_dblToken = dblOutput;
          sprintf_s(chrOutput,"%f",dblOutput);
          objOutput.m_strToken = chrOutput;
 
          this->ReplaceOp(arrObjCalcStack,intCurrPos - 2,intCurrPos,objOutput);
          blnCalcSuccessful = true;
          return 1;
 
      }else{
          blnCalcSuccessful = false;
          return 0;
      }
   }catch(...){
      blnCalcSuccessful = false;
      return -1;
   }//end try catch
 
};

The operation first performs a ValidOpInputs() to check and see if the correct inputs are there for the function in the stack. If valid, then the power calculation is performed. Next the ReplaceOp() is called replacing the operator and inputs with a single output number CSRpnUnit. It is recommended that the user follow this pattern (validate, calculate, replace). It is also recommended that in making a new function, just copy an existing function and change the name and inner workings. It is easier that way and the user will be less likely to forget something or make mistakes.