Introduction
This WPF C# .NET 4.5 code takes advantage of a 2-dimensional system of linear difference equations that gives a very fast implementation of generating large Fibinocci numbers (and Fibonacci numbers modulo N).
The Fibonacci numbers series starts 0,1,1,2,3,5,8,13,21,34,55,89.....
and is defined as: F[n] = F[n-2] + F[n-1]
They are found everywhere in mother nature and define the most efficient packing order of two dimensional objects:
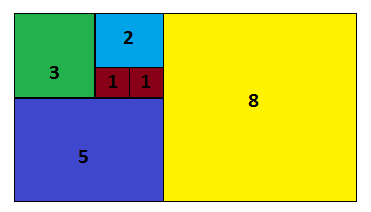
They have some interesting properties when it comes to prime numbers. In fact, the algorithm (in the code below) tests for primality. The first few pseudoprimes are: 4181, 5777, 6479, 6721.
The graph of the first 332 pseudoprimes looks like this:

(If you can create an algorithm to test for the pseudoprimes, please be sure to drop a line in the comments below. I'd be glad to investigate it.)
Also, the Fibonacci sequence can be used to calculate the golden ratio. This is because F[n+1] / F[n] approaches the golden ratio as n approaches infinity.
Background
While looking for new methods for integer factorization and primality testing, I stumbled accross the Fibonacci series and was thoroughly fascinated by its properties.
I've always wondered: is there an efficient way to calculate the index (i) of Fib(i) where Fib(i) modulo m is congruent to zero and the factors of m are unknown?
And what about calculating the index (i) where Fib(i) % m is positve or negative one (and the factors of m are unknown)?
Some Speed Tests
Fibonacci.Fib(1000000);
Takes ~ 9169 milliseconds.
Fibonacci.FibMod(BigInteger.Parse("1000000000000"), BigInteger.Parse("1000000000001")) ;
Takes ~ 2 milliseconds
Using the Code
You will need to reference System.Numerics in C# .NET 4.5 or higher.
This implementation makes use of some simple matrix operations for calculating Fibonacci numbers by index:
public static BigInteger Fib(BigInteger idx)
{
if (idx == 0) return 0;
if (idx == 1) return 0;
var m = new FibMatrix(1, 1, 1, 0);
m = m.RaiseMatrixByPower(idx - 1);
return m.Result();
}
The matrix is raised to a power (idx - 1) and the resultant value in cell location (0,0) is the Fibonacci value. The first few digits of the 1 millionth Fibonacci number is:
195328212870775773163201494759625633244354299659187339695340519457162525788701569476664198...
Also note, to calculate the golden ratio you can simply divide two consecutive Fibonacci numbers:
var dgs = BigInteger.Parse
("10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000");
var f1 = Fibonacci.Fib(10000);
var f2 = Fibonacci.Fib(10001) * dgs;
var rs = f2 / f1;
var tmp = rs.ToString();
which gives (after placing the decimal):
1.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374
The following method handles the modular reduction of our Fibonacci numbers by some divisor:
public static BigInteger FibMod(BigInteger idx, BigInteger divisor)
{
if (idx == 0) return 0;
if (idx == 1) return 0;
var m = new FibMatrix(1, 1, 1, 0);
m = m.RaiseMatrixByPowerMod(idx - 1, divisor);
return m.Result();
}
And it can be used to test for probable primality:
public static bool IsProbablePrime(BigInteger value)
{
if (value <= 6)
{
if (value == 2) return true;
if (value == 3) return true;
if (value == 5) return true;
return false;
}
if (value % 2 == 0) return false;
if (value % 3 == 0) return false;
if (value % 6 != 1 && value % 6 != 5) return false;
var md = FibMod(value, value);
var primeTest = false;
var res = value % 5;
if (res == 2 || res == 3)
{
if (md == (value - 1)) primeTest = true;
}
else
{
if (md == 1) primeTest = true;
}
return primeTest;
}
Notice that this is a "probable prime" test. That means if it returns "true", there's a strong possibility that the number being tested is prime. However, if it returns false, it's absolutely NOT a prime.
Also, if you are asked to calculate the last 5 digits of the 10,000th Fibonacci number:
var f1 = Fibonacci.FibMod(BigInteger.Parse("10000"), 100000);
which gives: 66875.
Points of Interest
- Consecutive Fibonacci numbers are the worst case scenario in Euclid's GCD problem
- Primality testing
- Pisano periods, totients, and integer factorization
- Possible to create a non-recursive method (to prevent stack overflows)
- Possible speedups that utilize multiple threads
Some Interesting Equations
- Golden Ratio = (1 + SQRT(5)) / 2
- F(n) = [(1 + SQRT(5))^n - (1 - SQRT(5))^n] / [2^n * SQRT(5)]
- GCD(F(m), F(n)) = F(GCD(m,n))
References
