Introduction
I needed to find the distance from a Point to a Bezier Segment. Turns out you need lot of Math tools. A polynomial class which can do simple math, derivate and find its roots. As well as Complex arithmentics.
The source can also be found on GitHub:
https://github.com/superlloyd/Poly
Using the code
There is a Complex.cs class which supports simple arithmetics. ex:
var c1 = 1 + 2 * Complex.I;
var c2 = c1 * c1;
var conjugate = !c1;
Assert.AreEquals(c2 / c1, c1);
There is a Polynomial.cs class which supports simple arithmetics, which is defined by listing its coefficient
var X = new Polynomial(0, 1);
var x2mx = X * (1 - X) + 1;
var x3 = new Polynomial(1,0,-1,2);
It also support Pow() Derivate() and Integrate()
var Xp1 = 1 + Polynomial.X();
var X2 = Xp1.Pow(2);
Assert.AreEquals(X1, new Polynomial(1,2,1))
var X = new Polynomial(0, 1);
var X2 = 1 + X + (X^3);
Assert.AreEquals(X2.Derivate(), 1+3*(X^2));
var X = new Polynomial(0, 1);
var X2 = 1 + X;
Assert.AreEquals(X2.Integrate(), X + (X^2)/2);
It also have its most interesting method: FindRoots()
public Complex[] FindRoots(int maxIteration = 10)
Which uses the Durand-Kerner algorithm:
http://en.wikipedia.org/wiki/Durand%E2%80%93Kerner_method
It's a very simple and quick algorithm which find all the root at once. The implementation is only 55 lines long!
It will be used later to calculate distance to a Bezier curves
I also added the Bezier curves equations:
http://en.wikipedia.org/wiki/B%C3%A9zier_curve
public static Polynomial LinearBezierCurve(double p0, double p1)
{
var T = new Polynomial(0, 1);
return p0 + T * (p1 - p0);
}
public static Polynomial QuadraticBezierCurve(double p0, double p1, double p2)
{
var T = new Polynomial(0, 1);
return (1 - T) * LinearBezierCurve(p0, p1) + T * LinearBezierCurve(p1, p2);
}
public static Polynomial CubicBezierCurve(double p0, double p1, double p2, double p3)
{
var T = new Polynomial(0, 1);
return (1 - T) * QuadraticBezierCurve(p0, p1, p2) + T * QuadraticBezierCurve(p1, p2, p3);
}
Distance to Bezier Segment
Now that I have all these basic math tools I can finally find the distance from a point to a Bezier segment!
If the curve equations is: BC(t),
The distance from P to the curve is the minimal distance of P to all the points BC(t).
To find the mimums of the distance I need to find the root / 0 of D'(t) (of the derivate of D(t))
Also t is between 0,1 for this reason I should also consider the segment extremities.
Which leave me with this very simple C# implementation of the distance:
public static double DistanceToBezier(this Point p, Point start, Point cp1, Point cp2, Point end)
{
var BX = Polynomial.CubicBezierCurve(start.X, cp1.X, cp2.X, end.X);
var BY = Polynomial.CubicBezierCurve(start.Y, cp1.Y, cp2.Y, end.Y);
var dsquare = (BX - p.X) * (BX - p.X) + (BY - p.Y) * (BY - p.Y);
var deriv = dsquare.Derivate().Normalize();
var deriveRoots = deriv.FindRoots();
return deriveRoots
.Where(x => Math.Abs(x.Imaginary) < Polynomial.Epsilon && x.Real > 0 && x.Real < 1)
.Select(x => (double)x.Real)
.Concat(new double[] { 0, 1 })
.Select(x => Math.Sqrt(dsquare.Compute(x)))
.OrderBy(x => x)
.First();
}
Points of Interest
Bezier curve and Polynomial.FindRoots() are implemented in a very clear and simple fashion. Thanks Wikipedia!
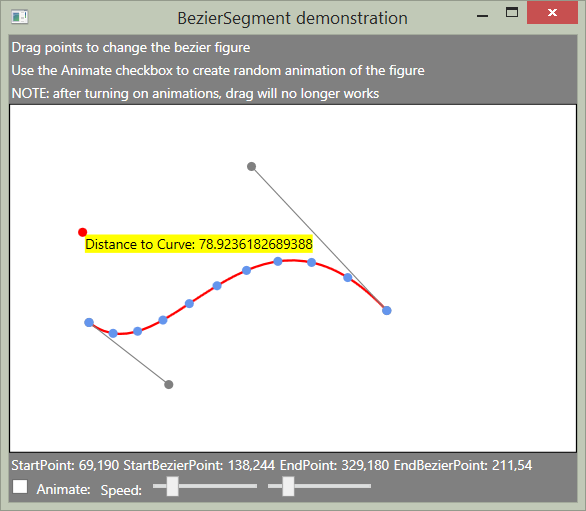
The code code with a Utility libray (including the unit tests) and a WPF application which show live calculated point and calculated distance.
I should thanks Jeremy Alles, as I used his application as the basis of my visual test application.
History
First release fo now...
Code change on GitHub: https://github.com/superlloyd/Poly
