Table of Contents
Problem Statement
In this blog, I'd like to apply the technique and software presented in my CodeProject article Simple Software for Optimal Control [1] to governance of a two-link manipulator. .NET code for the article provides solution for this problem. The mathematic model of the manipulator is taken from write-up A two-link manipulator: simulation and control design [2] by Stephen Dodds (advisor Dr. Mahboub Baccouch). It is expected that the reader is familiar with [1] since its terminology, notation and formulas are widely used here.
The simplified model of the two-link vertically oriented manipulator is depicted below [2].
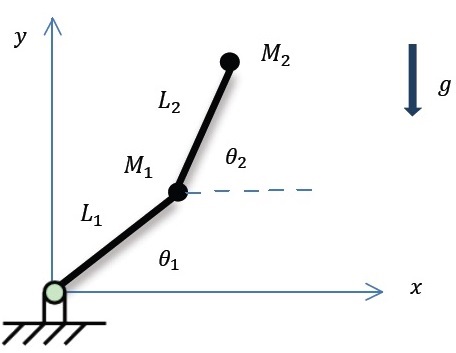 |
| Simplified model of a two-link manipulator |
Here Mi are lumped masses, Li are lengths of the links and Θi are links' displacement angles. Math description of the model is given with formulas (1).
The system is essentially nonlinear. For its optimal control, we will apply method of linear-quadratic control combined with quasilinearization and appropriate software provided in [1].
According to notation used in [1], state vector x corresponds to vector z in (1). The system is actuated with two motors producing torques T1 and T2 rotating the links. For the sake of simplicity, it is assumed that the motors are inertialess. Control vector m of dimension 2 corresponds to the torques. The torques are denotes as fΘ1 and fΘ2 in formulas (1).
Our goal is to suggest such control of the system which provides transition from its initial position to a prescribed final position and its fixation in the final position. The transition should be fast. However, during this transition values of angular velocities and torques should be kept within some reasonable limits to avoid damage of system's mechanics.
For numerical sample, it is assumed masses in kg, lengths in m, time in s and torques in N⋅m. Therefore g = 9.81 m/s2. Angles are assumed in degrees for a better reading. The following parameters are taken for numeric sample:
Δt = 0.01, N = 1001.
Optimization Policies
The goal spoken out above should be formalized. The suggested approach is to minimize integral quadratic cost function described in [1]. Below, we demonstrate application of two optimization policies to the system. The case 1 is characterized with:
- permanent desirable final values for Θ1 and Θ2 angles which are desirable coordinates r0 and r2 respectively,
- permanent weight factors for the Θ-s as Q00 and Q22, and
- permanent limits to external control parameters (torques) implemented with unit matrix Z and zero vector u.
The case 2 implies:
In both cases, we confine ourselves with just one iteration enabling in conjunction with constant weight matrices to achieve constant values of feedbacks.
These two optimization policies are applied to the following two movements.
Movements
The first movement
| xinit = | $ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} $ | , | xfinal = | $\begin{bmatrix} 45 \\ 0 \\ 30 \\ 0 \end{bmatrix}$ |
and
The second movement
| xinit = | $ \begin{bmatrix} 45 \\ 0 \\ 30 \\ 0 \end{bmatrix} $ | , | xfinal = | $\begin{bmatrix} 60 \\ 0 \\ -30 \\ 0 \end{bmatrix}$ |
The First Movement
Input
Case 1
$ Q = \begin{bmatrix} 5000 &0 &0 &0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 5000 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , Z = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , r = \begin{bmatrix} 48.5 \\ 0 \\ 32 \\ 0 \end{bmatrix} , u = 0$
Case 2
$ Q = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} , Z = 0 , r = \begin{bmatrix} (2)where \hspace{2 mm} s=0.6, r_{final}=48.6\\ 0 \\ (2)where \hspace{2 mm} s=0.6, r_{final}=32\\ 0 \end{bmatrix} $
Result Transients
 |
| Θ1 |
 |
| dΘ1/dt |
 |
| T1 |
 |
| Θ2 |
 |
| dΘ2/dt |
 |
| T2 |
The Second Movement
Input
Case 1
$ Q = \begin{bmatrix} 5000 &0 &0 &0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 5000 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , Z = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , r = \begin{bmatrix} 66.5 \\ 0 \\ -19 \\ 0 \end{bmatrix} , u = 0$
Case 2
$ Q = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} , Z = 0 , r = \begin{bmatrix} (2) where \hspace{2 mm} s=0.6, r_{final}=66.5\\ 0 \\ (2) where \hspace{2 mm} s=0.6, r_{final}=-20.5\\ 0 \end{bmatrix} $
Result Transients
 |
| Θ1 |
 |
| dΘ1/dt |
 |
| T1 |
 |
| Θ2 |
 |
| dΘ2/dt |
 |
| T2 |
Calculated Feedbacks and Permanent Inputs of Close-Loop System
Case 1
Feedback
| 46.7 | 7.07 | -46.6 | -7.06 |
| 46.6 | 7.06 | 46.6 | 7.06 |
Input for the First Movement
Input for the Second Movement
Case 2
Feedback
| 49.9 | 50.5 | -49.8 | -50.5 |
| 49.7 | 50.5 | 49.8 | 50.5 |
Although formally in the case 2 input of close-loop system is not constant, calculations show results very close to the constant values below.
Input for the First Movement
Input for the Second Movement
Discussion
Problem of two-link manipulator optimal control is not a simple one. The system is essentially nonlinear. Its solution requires effective coordinated control by two channels (torques). As it is shown above, the technique for minimization of integral quadratic cost function presented in [1] allows designer to easily calculate various control policies. In fact, I performed a lot of calculations with various values of desirable vectors and weight matrices members, and the above results constitute just a small part of them. For both discussed sets of input data, we managed to obtain reasonable control policies with just one iteration ensuring constant value of feedbacks. It is interesting that obtained control policies include positive feedbacks from angle and angular velocity of the second link to the first actuator in both control cases. Both control channels have similar feedback values because masses M1 and M2 and link lengths L1 and L2 are equal.
For further research, check the system controlled with suggested policies for stability and sensitivity to model inaccuracy is required. And of course, it is always interesting to generate more control policies, e.g., with more that one iterations process. For technical implementation of control will be useful to provide effective measurement / estimation of feedback parameters (that are links angles and angular velocities). For the real life system dynamics of actuators should be included to mathematical model of controlled object.
