Introduction
What is Gamma Function?
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers (look at Wikipedia).
Simple Explanation: What is the factorial of non-Integer number? The answer is gamma function!
In this tip, I show you how to calculate gamma function. Simple, fast and accurate!
Background
First of all, you need to know some basic rules about factorials:
- Γ(x) = (x - 1)!
- x! = (x -1)! * x
- x! = (x+1)! / x
To calculate gamma function, we use taylor series.
Note: taylor series does not converge fast enough for all real numbers. So, we expand this series at the range of numbers between -1 and 1. stepping size is 0.05 and we calculate 9 terms of series to achieve high precision.
This is the taylor series of x! (look at Wolframalpha).
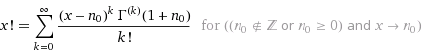
where n0 is expansion point and Γ(k) is the kth derivative of gamma function.
Note: As you choose n0 closer to x, you will get more accurate results. Thus, choose the closest n0 to x.
Note: Γ(k) (1 + n0)/ k! is a constant so we precalculate all these values and keep them in arrays.
Note: To calculate Γ(x), for x between -1 and 1, use taylor series directly.
Note: To calculate Γ(x), for x more than 1 or less than -1, first use factorial rules to shift x between -1 and 1, then multiply result by Γ(x) using series.
Using the Code
Store all precalculated Gamma derivatives inside arrays.
Initialize arrays once. Because these arrays are constant, so mark them as readonly.
You will have 41 arrays (because -20 < x / 0.05 < 20), each array has a length of 10.
First index is n0 and rest of the arrays are constant part of 9 terms of the series.
Since step size is 0.05, we should choose the array that is closest to the x.
For example, when x = 0.5784, then we have x/0.05=11.568 therefore we choose 11th or 12th array.
static class GammaDerivative
{
private static readonly double[]
GammaDerivativesRange20N =
{
0D, Double.NaN, 0D, 0D, 0D, 0D, 0D, 0D, 0D, 0D
};
private static readonly double[]
GammaDerivativesRange19N = {
-0.95, 19.4700853112555D, -399.0947906775D,
7999.22620441159D, -159999.192130127D,
3199999.2329081D, -63999999.259529D, 1279999999.29272D, -25599999999.3247D,
511999999999.356D
};
private static readonly double[]
GammaDerivativesRange18N = {
-0.90, 9.51350769866873D, -99.166472874637D,
999.336741961287D, -9999.32866773128D,
99999.3941978608D, -999999.440326772D, 9999999.48975095D, -99999999.5347559D,
999999999.576533D
};
private static readonly double[]
GammaDerivativesRange17N = {
-0.85, 6.22027287404988D, -43.6724944505672D,
295.725305699639D, -1974.74565909015D,
13168.2411259365D, -87791.0668614162D, 585276.261230467D, -3901843.90519612D,
26012294.5899988D
};
private static readonly double[]
GammaDerivativesRange16N = {
-0.80, 4.5908437119988D, -24.281155551781D,
124.506711961476D, -624.523806406947D,
3124.61123747756D, -15624.6683906425D, 78124.723097606D, -390624.768282098D,
1953124.80661177D
};
private static readonly double[]
GammaDerivativesRange15N = {
-0.75, 3.62560990822191D, -15.3270974171567D,
63.5726995550479D, -255.593913429678D,
1023.68469107349D, -4095.74053268546D, 16383.7921939606D, -65535.8329260497D,
262143.866126271D
};
private static readonly double[]
GammaDerivativesRange14N = {
-0.70, 2.99156898768759D, -10.4780428417585D, 36.6662258367875D, 123.107763832927D,
411.265075256399D, -1371.53707456811D, 4584.60422680214D, -653.188004194767D,
1905.18212638032D
};
private static readonly double[]
GammaDerivativesRange13N = {
-0.65, 2.54614697721229D, -7.56478311429081D,
23.0015368028935D, -66.3366289787721D,
190.18514185276D, -543.82748921185D, 1574.64401643923D, -222.01988683161D, 555.081610140393D
};
private static readonly double[]
GammaDerivativesRange12N = {
-0.60, 2.21815954375769D, -5.68155957280492D, 15.3452802672229D, -38.7987670035651D,
97.4812519180141D, -244.009046282463D, 610.258055159647D, -1525.81152787317D,
3814.64906436589D
};
private static readonly double[]
GammaDerivativesRange11N = {
-0.55, 1.96813640060238D, -4.39590870900005D,
10.7313082744161D, -24.1547234259443D,
54.046946033126D, -120.320539267501D, 267.543235620895D, -594.651805969081D,
1321.52636874769D
};
private static readonly double[]
GammaDerivativesRange10N = {
-0.50, 1.77245385090552D, -3.48023090691326D,
7.79008872120313D, -15.7947670515358D,
31.8788248211608D, -63.9126957469214D, 127.942612101477D, -255.961228074064D,
511.974131361039D
};
private static readonly double[]
GammaDerivativesRange9N = {
-0.45, 1.61612426873358D, -2.80552587449537D,
5.82967843679375D, -10.7451701862446D,
19.7681401306886D, -36.054376432714D, 65.6387780703025D, -119.396066949852D,
217.118739506589D
};
private static readonly double[]
GammaDerivativesRange8N = {
-0.40, 1.48919224881282D, -2.29427819170183D,
4.47481216055898D, -7.55158129739921D,
12.7751466003399D, -21.3737135387477D, 35.6862016537667D, -59.5142819897528D,
99.2145860007862D
};
private static readonly double[]
GammaDerivativesRange7N = {
-0.35, 1.38479510202651D, -1.89765322148743D,
3.50997923688594D, -5.45315568098083D,
8.54726981248489D, -13.2092750442655D, 20.3698140233823D, -31.3648094688375D,
48.2704560546125D
};
private static readonly double[]
GammaDerivativesRange6N = {
-0.30, 1.29805533264756D, -1.58365807983323D,
2.80542638961667D, -4.02911317569611D,
5.89012621801116D, -8.4577012051428D, 12.1192152879838D, -17.3323878441919D,
24.772584430011D
};
private static readonly double[]
GammaDerivativesRange5N = {
-0.25, 1.22541670246518D, -1.33063205864388D,
2.27987153689211D, -3.03563250547648D,
4.16393568279721D, -5.58283545990313D, 7.47255601476381D, -9.97739134364727D,
13.3118755327171D
};
private static readonly double[]
GammaDerivativesRange4N = {
-0.20, 1.1642297137253D, -1.12349164735875D,
1.88064759057317D, -2.32570573138395D,
3.00999174853583D, -3.78401986966253D, 4.75293897617795D, -5.95139905960929D,
7.44560973380385D
};
private static readonly double[]
GammaDerivativesRange3N = {
-0.15, 1.11248373694847D, -0.951474631732596D,
1.57262112883441D, -1.8076083166106D,
2.21911024240823D, -2.62497750703055D, 3.10679421302081D, -3.66254589040758D,
4.313599542982D
};
private static readonly double[]
GammaDerivativesRange2N = {
-0.10, 1.06862870211932D, -0.806736606716814D,
1.33175429379401D, -1.42237555998628D,
1.66505223223746D, -1.85860162426187D, 2.08047822528401D, -2.31712549060625D,
2.57813819793116D
};
private static readonly double[]
GammaDerivativesRange1N = {
-0.05, 1.03145331712903D, -0.683450886596578D,
1.14123138250983D, -1.1310941970201D,
1.26930701966673D, -1.34008996998964D, 1.42357900301788D, -1.50248828254655D,
1.58428059433746D
};
private static readonly double[]
GammaDerivativesRange0 = {
0.00, 1D, -0.577215664901533D, 0.989055995327973D,
-0.907479076080886D, 0.9817280868344D,
-0.981995068903145D, 0.993149114621276D, -0.996001760442431D, 0.998105693783129D
};
private static readonly double[]
GammaDerivativesRange1 = {
0.05, 0.973504265562776D, -0.484654222619487D,
0.866519543079475D, -0.733402094741922D,
0.76951527826578D, -0.730068352575782D, 0.705106859611967D, -0.673517910757183D,
0.643103417607824D
};
private static readonly double[]
GammaDerivativesRange2 = {
0.10, 0.951350769866873D, -0.403139588794969D,
0.767201321491692D, -0.596124811841251D,
0.610752054797181D, -0.54983481640542D, 0.508648322752892D, -0.4637246400447D,
0.422897453990549D
};
private static readonly double[]
GammaDerivativesRange3 = {
0.15, 0.933040931107482D, -0.330601293535208D,
0.68630140437857D, -0.486543163883966D,
0.490509800318163D, -0.418903275959234D, 0.372323153930381D, -0.324548950953126D,
0.28330369492238D
};
private static readonly double[]
GammaDerivativesRange4 = {
0.20, 0.918168742399761D, -0.265387398357406D,
0.620186840514084D, -0.39804931991382D,
0.398441088563801D, -0.322440650940798D, 0.276228878711926D, -0.230558813523784D,
0.19304025682217D
};
private static readonly double[]
GammaDerivativesRange5 = {
0.25, 0.906402477055477D, -0.206164446067268D,
0.566077471605273D, -0.325778802371648D,
0.327259338693816D, -0.250442097877781D, 0.20751580468742D, -0.166037551807169D,
0.133605517985885D
};
private static readonly double[]
GammaDerivativesRange6 = {
0.30, 0.897470696306277D, -0.151843864839965D,
0.521824909277723D, -0.266103313090753D,
0.271758743992428D, -0.196047114034794D, 0.157734240896269D, -0.121073949387992D,
0.0938120535339359D
};
private static readonly double[]
GammaDerivativesRange7 = {
0.35, 0.891151442024301D, -0.101527112789497D,
0.485754766721896D, -0.216283339676781D,
0.228170669693991D, -0.154479371387366D, 0.121233525593135D, -0.0893005718326651D,
0.0667563410353867D
};
private static readonly double[]
GammaDerivativesRange8 = {
0.40, 0.887263817503075D, -0.0544642853642779D,
0.456552534084234D, -0.174226534203179D,
0.193733763640491D, -0.122366594971248D, 0.0941757813954528D, -0.0665559896195936D,
0.0480978731915532D
};
private static readonly double[]
GammaDerivativesRange9 = {
0.45, 0.885661380271072D, -0.0100225184476424D,
0.433180014487195D, -0.138317267258814D,
0.166402288962429D, -0.0972966372492549D, 0.0739167619019626D, -0.0500770651916732D,
0.0350599673777081D
};
private static readonly double[]
GammaDerivativesRange10 = {
0.50, 0.886226925452758D, 0.032338397448885D, 0.414813453688301D, -0.107294804564772D,
0.144645359044622D, -0.0775230522998542D, 0.0586103038171763D, -0.0380019355548651D,
0.0258376064557562D
};
private static readonly double[]
GammaDerivativesRange11 = {
0.55, 0.888868347803466D, 0.0730850377611226D,
0.400797265741192D, -0.0801651656407642D,
0.127306885634156D, -0.0617669073040915D, 0.0469515059524152D, -0.0290587521158863D,
0.0192397787722501D
};
private static readonly double[]
GammaDerivativesRange12 = {
0.60, 0.89351534928769D, 0.112625333791716D,
0.390609104633555D, -0.0561366178805398D,
0.113506662804717D, -0.0490815229087629D, 0.0380074535123248D, -0.0223675400849471D,
0.0144696107189241D
};
private static readonly double[]
GammaDerivativesRange13 = {
0.65, 0.900116816317232D, 0.151320508059681D,
0.383833282488433D, -0.0345719557515931D,
0.102569697134353D, -0.0387589662876536D, 0.0311040709330098D, -0.0173121313620963D,
0.0109869666606985D
};
private static readonly double[]
GammaDerivativesRange14 = {
0.70, 0.90863873285329D, 0.189494676764298D,
0.380140392898439D, -0.0149528333706117D,
0.0939751769116959D, -0.0302646255888054D, 0.025749496445827D, -0.0134562029505838D,
0.00842125681577184D
};
private static readonly double[]
GammaDerivativesRange15 = {
0.75, 0.919062526848883D, 0.227442658482271D,
0.379271594025204D, 0.00314715778474762D,
0.0873192566214339D, -0.0231909121301314D, 0.0215815511697291D, -0.010487492971643D,
0.00651530589057573D
};
private static readonly double[]
GammaDerivativesRange16 = {
0.80, 0.931383770980243D, 0.265436395838301D,
0.38102642509978D, 0.0200830054660084D,
0.0822876674447171D, -0.0172241471941937D, 0.0183313112798304D, -0.0081802715094781D,
0.00508872743379526D
};
private static readonly double[]
GammaDerivativesRange17 = {
0.85, 0.945611176406195D, 0.303730299975759D,
0.385253327776652D, 0.0361540597154019D,
0.0786353894364008D, -0.012120638567738D, 0.0157975740371346D, -0.00636979382563056D,
0.00401372112712226D
};
private static readonly double[]
GammaDerivativesRange18 = {
0.90, 0.961765831907387D, 0.342565756074187D,
0.391842257697791D, 0.0516162898063564D,
0.0761714490274338D, -0.00768922959822524D, 0.0138287784937392D, -0.00493471626161532D,
0.00319888753179316D
};
private static readonly double[]
GammaDerivativesRange19 = {
0.95, 0.979880651272581D, 0.382174974862283D,
0.400718926787762D, 0.0666918953407411D,
0.0747474716632996D, -0.00377845182343007D, 0.0123100828773469D, -0.00378486540133988D,
0.0025782820740309D
};
private static readonly double[]
GammaDerivativesRange20 =
{
0D, 1D, 0D, 0D, 0D, 0D, 0D, 0D, 0D, 0D
};
public static double[] GetGammaArray(double x)
{
switch ((int) (x / 0.05))
{
case -20:
return GammaDerivativesRange20N;
case -19:
return GammaDerivativesRange19N;
case -18:
return GammaDerivativesRange18N;
case -17:
return GammaDerivativesRange17N;
case -16:
return GammaDerivativesRange16N;
case -15:
return GammaDerivativesRange15N;
case -14:
return GammaDerivativesRange14N;
case -13:
return GammaDerivativesRange13N;
case -12:
return GammaDerivativesRange12N;
case -11:
return GammaDerivativesRange11N;
case -10:
return GammaDerivativesRange10N;
case -9:
return GammaDerivativesRange9N;
case -8:
return GammaDerivativesRange8N;
case -7:
return GammaDerivativesRange7N;
case -6:
return GammaDerivativesRange6N;
case -5:
return GammaDerivativesRange5N;
case -4:
return GammaDerivativesRange4N;
case -3:
return GammaDerivativesRange3N;
case -2:
return GammaDerivativesRange2N;
case -1:
return GammaDerivativesRange1N;
case 0:
return GammaDerivativesRange0;
case 1:
return GammaDerivativesRange1;
case 2:
return GammaDerivativesRange2;
case 3:
return GammaDerivativesRange3;
case 4:
return GammaDerivativesRange4;
case 5:
return GammaDerivativesRange5;
case 6:
return GammaDerivativesRange6;
case 7:
return GammaDerivativesRange7;
case 8:
return GammaDerivativesRange8;
case 9:
return GammaDerivativesRange9;
case 10:
return GammaDerivativesRange10;
case 11:
return GammaDerivativesRange11;
case 12:
return GammaDerivativesRange12;
case 13:
return GammaDerivativesRange13;
case 14:
return GammaDerivativesRange14;
case 15:
return GammaDerivativesRange15;
case 16:
return GammaDerivativesRange16;
case 17:
return GammaDerivativesRange17;
case 18:
return GammaDerivativesRange18;
case 19:
return GammaDerivativesRange19;
case 20:
return GammaDerivativesRange20;
}
return null;
}
}
Note: double is floating point so sometimes method will not correctly select array (example: it will choose next or previous array), but it will not affect the result more than Epsilon!
Note: If range equals to -20 or 20 means x was Integer. If you notice, we have two more arrays: GammaDerivativesRange20 and GammaDerivativesRange20N. These arrays are filled with 0 and contain exception.
GammaDerivativesRange20N[1] = Double.NaN
GammaDerivativesRange20 [1] = 1
The main Factorial and Gamma method:
public static double Gamma(double x)
{
return (x - 1d).Factorial();
}
public static double Factorial(this double x)
{
if (x.Equals(Double.NaN)) return Double.NaN;
if (x >= 170.602544778489474d)
return Double.PositiveInfinity;
if (x <= -178.477785816716264d) return System.Math.Abs((x - (int) x))
< Double.Epsilon? Double.NaN : 0;
or 0(for non-Integer)
var resault = 1d;
if (x > 0) while (x > 1) resault *= x--;
else while (x < -1) resault /= ++x;
var gammaDerivativesRange = GammaDerivative.GetGammaArray(x);
x -= gammaDerivativesRange[0];
return
((((((((gammaDerivativesRange[9]*x + gammaDerivativesRange[8])*x + gammaDerivativesRange[7])*x +
gammaDerivativesRange[6])*x + gammaDerivativesRange[5])*x + gammaDerivativesRange[4])*x +
gammaDerivativesRange[3])*x + gammaDerivativesRange[2])*x +
gammaDerivativesRange[1])*resault;
}
Run the code:
static void Main()
{
Console.WriteLine(Gamma(Double.Parse(Console.ReadLine())));
}
Compare results at www.wolframalpha.com !
Accuracy
With taylor series expanded at 41 different points up to 9 terms, this algorithm will give you 15 decimal parts all correct!
Performance
For optimization i - introduced arrays inside class and initialized them once. Performance difference: about 0.08 secs.
- Used expression when returning result except for using
for loop. Performance difference is about 3.5 secs !! - Used parenthesis inside expression: Performance difference: about 1 sec !
- Removed separate factorial algorithm for integer numbers. Performance difference: about 0.5 secs
- Used Horners rule for evaluating expression: Performance difference: about 0.05 secs
(Thanks to YvesDaoust for his suggestion.)
Take a look at this benchmark.
static void Main()
{
for (int i = 0; i < 10; i++)
{
var timer = new Stopwatch();
timer.Start();
for (var j = -10d; j < 10d; j += 0.000001)
{
var r = Math.Factorial(j);
}
Console.WriteLine(timer.Elapsed);
}
}
Results:
00:00:00.5542497
00:00:00.5417712
00:00:00.5415342
00:00:00.5416845
00:00:00.5418725
00:00:00.5413725
00:00:00.5441604
00:00:00.5412434
00:00:00.5402805
00:00:00.5426584
History
- Returning final result expression changed based on horners scheme (thanks to YvesDaoust!)
- Added exception for
double.NaN inputs - A few changes to
switch case, removed if else condition
