Parametric Curves and Surfaces in the Public Domain Geometry Utilities Library

Introduction

This page describes parametric curves and surfaces and how to generate them using my public-domain Geometry Utilities Library.

Source code for the latest version of the library is available at the Geometry Utilities Library's project page.

Contents

• Introduction
• Contents
• What Is a Parametric Surface?
  • Why Two Variables?
• Parametric Surfaces in the Geometry Utilities Library
• Chaining Surface Functions
• Parametric Curves
  • Generating Parametric Curves
• Curve and Surface Evaluators in the Geometry Utilities Library
• Other Pages

What Is a Parametric Surface?

A parametric surface is a surface generated by evaluating the results of a vector function. This vector function takes two numbers, U and V, and returns a 3D point, X, Y, and Z. Each (U, V) point corresponds to an (X, Y, Z) point that lies on the surface.

A vector function in 3D is a combination of three functions, one for each dimension:

• F(u, v) = [ x(u, v), y(u, v), z(u, v) ];

The x function returns an X coordinate given u and v, and likewise for y and z. Since the z function returns a Z coordinate, the surface will be in 2D if z always returns the same value.

For example, if we have a parametric surface defined by the following functions:

• x(u, v) = u * v
• y(u, v) = -u
• z(u, v) = u * sqrt(v)

and we evaluate the UV point (2, 4), then we have:

• F(2, 4) = [ 2 * 4, -2, 2 * sqrt(4) ];
• F(2, 4) = [ 8, -2, 4 ];

So (8, -2, 4) is one point that lies on this parametric surface, and any other point on the surface can be found by evaluating different UV points. By the way, the surface looks like this:

Why Two Variables?

The surface functions take two variables, u, and v, because a parametric surface can be a seen as a "warped" version of a rectangular grid. The vector function "warps" this grid into a three-dimensional surface.

Parametric Surfaces in the Geometry Utilities Library

The Geometry Utilities Library supports parametric surfaces using a class named SurfaceBuilder. It helps generate vertex coordinates and other attributes using a parametric surface function. The following helper function, makeMesh, generates a parametric surface mesh. The comments explain how makeMesh works in detail.

function makeMesh(func,resolutionU, resolutionV){
   "use strict";
   if(typeof resolutionV === "undefined" || resolutionV === null)resolutionV = resolutionU;
   if(typeof resolutionU === "undefined" || resolutionU === null)resolutionU = 50;
   if(typeof resolutionV === "undefined" || resolutionV === null)resolutionV = 50;
      // define a color gradient evaluator for
      // demonstration purposes. Instead of X, Y, and Z,
      // generate a Red/Green/Blue color based on
      // the same parameters U and V as the surface
      // function for 3D points.
   var colorGradient = {
     "evaluate":function(u, v) {
       return [1 - u, v, u];
     }
   };
   return new H3DU.SurfaceBuilder()
      .positionNormal(func)
      .attribute(colorGradient, H3DU.Semantic.COLOR)
     // Evaluate the surface and generate a triangle
     // mesh, using resolution+1 different U coordinates,
     // and resolution+1 different V coordinates.
     // Instead of H3DU.Mesh.TRIANGLES, we could use
     // H3DU.Mesh.LINES to create a wireframe mesh,
     // or H3DU.Mesh.POINTS to create a point mesh.
      .evalSurface(H3DU.Mesh.TRIANGLES, resolutionU, resolutionV)
      .toMeshBuffer();
}

In the Geometry Utilities Library, surface evaluator objects define a method, evaluate, which returns a 3D point given a U parameter and a V parameter. (By default, U and V each range from 0 through 1.)

The following code is a very simple surface evaluator object.

var evaluator = {
  "evaluate":function(u, v){
    // Take the U parameter as the X coordinate,
    // the V parameter as the Y coordinate, and 0 as
    // the Z coordinate.
    return [u, v, 0];
  }
};

That evaluator simply generates a square at the top-right quadrant:

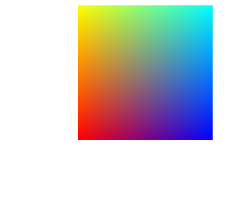
And the following evaluator generates a circular disc:

var evaluator = {
  "evaluate":function(u, v){
     // Return disc coordinates.
     return [u*Math.cos(v),u*Math.sin(v),0];
  },
  // Declare the usual range of the coordinates
  "endPoints":function(){ return [0,1,0,Math.PI*2]; }
};

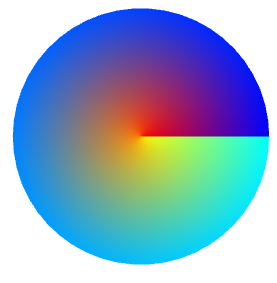
Now here's the interesting part: This evaluator returns not a disc, but a cone, whose length runs along the negative Z axis:

var evaluator = {
  "evaluate":function(u, v){
     // Return cone coordinates, using the u
     // parameter as the Z axis.
     return [u*Math.cos(v),u*Math.sin(v),-u];
  },
  // Declare the usual range of the coordinates
  "endPoints":function(){ return [0,1,0,Math.PI*2]; }
};

The following shape was rotated to show the Z axis; the rotation isn't perfect.

Note that all three examples above use a value named evaluator. A mesh buffer for the surface evaluator can be generated using something like the following:

var meshBuffer = SurfaceBuilder.surfaceToBuffer(evaluator);

The generated 3D mesh buffer from a parametric surface is just like any other mesh buffer, and the same functions and methods you use for other mesh buffers can be used on this mesh buffer as well. For more information, see the API references for the H3DU.MeshBuffer and Shape classes.

Chaining Surface Functions

The technique of using surface evaluator objects is very flexible. In fact, you can chain evaluators, using the output of one evaluator as the input of another evaluator. This can be used to transform the surface's points to new positions.

As an example, we'll define a new evaluator that shifts the position of a parametric surface. It takes an existing surface evaluator and the X, Y, and Z of how many units to shift the surface. Note that this class includes its own evaluate method, allowing itself to be passed to the H3DU.SurfaceBuilder class's method or the makeMesh method above.

function SurfaceShifter(evaluator, x, y, z) {
 // Shift the surface by X units.
 this.x = x;
 // Shift the surface by Y units.
 this.y = y;
 // Shift the surface by Z units.
 this.z = z;
 this.evaluator = evaluator;
 // Define the surface shifter function
 this.evaluate = function(u, v){
  // Get the coordinates from the source evaluator
  var retval = this.evaluator.evaluate(u, v);
  // Shift the coordinates
  retval[0]+=this.x;
  retval[1]+=this.y;
  retval[2]+=this.z;
  // And return the new coordinates.
  return retval;
 }
 this.endPoints=function(){
  return this.evaluator.endPoints()
 }
}

And here's an example of its use. We'll take the disc surface given above, and create a SurfaceShifter object that shifts the disc by 3 units horizontally and vertically (by default, the disc will be centered at the origin (0, 0, 0)).

// This is the disc surface from before
var evaluator = {
  "evaluate":function(u, v){
     // Extend the range of v
     v*=Math.PI*2;
     // Return circle coordinates.
     return [u*Math.cos(v),u*Math.sin(v),0];
  },
  "endPoints":function() { return [0,Math.PI*2] }
}
// Create a shifter that results in the circle being moved 3 units
// up and 3 units to the right
evaluator = new SurfaceShifter(evaluator, 3, 3, 0);

Parametric Curves

The Geometry Utilities Library also includes support for generating parametric curves. A parametric curve is a curve generated by a vector function, like a parametric surface, except now, the function only uses a single variable, as shown below:

• C(u) = [ x(u), y(u), z(u) ];

As before, the x, y, and z functions return the corresponding coordinates of the curve. And each (U) point corresponds to an (X, Y, Z) point that lies on the curve.

The curve function takes a single u variable because a parametric curve can be a seen as a "warped" version of a line.

One simple example of a parametric curve is a circle. In fact, the same source code for the disc surface given above can also serve as the parametric curve function for the circle, since it only uses the variable u, not v.

Note that any surface evaluator that only uses u can easily serve as a parametric curve evaluator, and so can any surface in which the v parameter is kept to the same value, such as 0, 1, or any other constant number.

Generating Parametric Curves

The Geometry Utilities Library's CurveBuilder class generates vertices for a parametric curve.

Use code like the following to generate a mesh describing a parametric curve. It assumes that evaluator is a parametric curve object, just like the circle example above.

var meshBuffer = CurveBuilder.curveToBuffer(evaluator);

Curve and Surface Evaluators in the Geometry Utilities Library

The Geometry Utilities Library distribution includes the following evaluators of curves and surfaces. All the classes named below include an evaluate method that returns 3D points lying on the curve or surface.

General-purpose curves include:

• B-spline curves. These curves consist of control points (which control the shape of the curve but don't necessarily lie on the curve), and a knot vector, which controls the behavior of the control points. B-spline curves include NURBS curves (nonuniform and rational B-spline curves, with weights and non-uniform knots), making them a powerful way of setting the behavior of a curve. B-Spline curves are created using the BSplineCurve class.
• Bézier curves. These are curves in which the first and last control point are the curve's end points. Bézier curves are a subset of B-spline curves and are created using the BSplineCurve.fromBezierCurve method.
• Piecewise curves. These are curves made up of one or more other curves. Piecewise curves are created using the PiecewiseCurve class.

General-purpose surfaces include:

• Bézier surfaces. 3D surfaces where each grid line is a Bézier curve. Bézier surfaces are created using the BSplineSurface.fromBezierSurface method.
• B-Spline surfaces. 3D surfaces where each grid line is a B-Spline or NURBS curve. B-Spline surfaces are created using the BSplineSurface class.

Special surfaces include:

• Tubes. 3D surfaces in the form of a "thickened" 3D curve. Tubes are created using the CurveTube class, a supplemental extra in the Geometry Utilities Library.
• Surfaces of revolution. Surfaces generated by rotating a 2D curve. Surfaces of revolution are created using the SurfaceOfRevolution class, a supplemental extra in the Geometry Utilities Library.

Other Pages

The following pages of mine on CodeProject also discuss the Geometry Utilities Library, formerly the Public-Domain HTML 3D Library:

• Public-Domain HTML 3D Library
• Creating shapes using the Public Domain HTML 3D Library
• The "Camera" and the Projection and View Transforms
• Graphics Filters for the HTML 3D Canvas