Graph is everywhere

The traditional way to solve the ZigZag Conversion problem is to either build a 2d table or find a pattern among the index of the letters on the same row. There is also a beautiful solution which builds on top of the BFS(Breadth First Search).

Problem

The string "PAYPALISHIRING" is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)

P   A   H   N
A P L S I I G
Y   I   R

And then read line by line: "PAHNAPLSIIGYIR"

Write the code that will take a string and make this conversion given a number of rows:

string convert(string text, int nRows);

convert("PAYPALISHIRING", 3) should return "PAHNAPLSIIGYIR".

Breadth First Search

Make each letter in the string a node in the graph. If we link the nodes following the order in the original string, we actually build a graph. Each node can have at most two neighbors. The order of the letters in the original string is actually result of DFS(Depth First Search) on this graph.

E.g.,  for string “ABCDE”,

A   E
B D
C

the resultant graph is as follows. We create some virtual paths between the nodes on the first row and the Root.

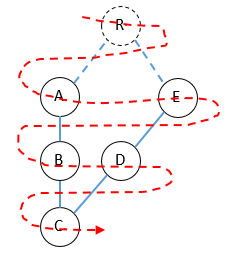
The BFS walk produces “AEBDC”, which is exactly what we want.

Just one thing left. What if the node “E” doesn’t exist?  For the last branch (e.g., it’s C->D here), we may need to create a virtual path to connect to the Root as show below.

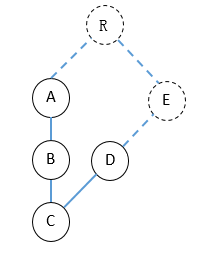
Here comes the code.

from collections import deque

class Node:
    def __init__(self, value):
        self.visited = False
        self.value = value
        self.neighbors = []

class Solution:
    # @param {string} s
    # @param {integer} numRows
    # @return {string}
    def convert(self, s, numRows):
        self.__s = s
        self.__numRows = numRows
        return self.__BFS(self.__buildGraph())

    def __connect(self, prev, this):
        prev.neighbors.append(this)
        this.neighbors.append(prev)

    def __buildGraph(self):
       '''Build the graph from DFS traversal of the string'''
       root = Node('')
       prev = None
       row = 0
       up = True
       for i in range(len(self.__s)):
           this = Node(self.__s[i])
           if prev is not None:
               self.__connect(prev, this)
           prev = this
           # Connect nearest nodes(those on row #0) to the root
           if row == 0:
               self.__connect(root, this)

           if up:
               if row < self.__numRows - 1:
                   row += 1
               elif row > 0:
                   row -= 1
                   up = False
           else:
               if row > 0:
                   row -= 1
               elif row < self.__numRows - 1:
                   row += 1
                   up = True

       # The triky part, for BFS later
       # Build a virtual path to connect to the root for the last branch, if not already
       if not up and row < self.__numRows - 2:
           for i in range(row, -1, -1):
               this = Node('')
               self.__connect(prev, this)
               prev = this
           self.__connect(prev, root)

       return root

 def __BFS(self, root):
     '''Breadth First Search gives the desired string'''
     work_queue = deque()
     root.visited = True
     work_queue.append(root)

     s = ''
     while work_queue:
         node = work_queue.popleft()
         # No special action for the root as it is an empty string;)
         s += node.value
         for i in node.neighbors:
             if not i.visited:
             i.visited = True
             work_queue.append(i)
     return s