C++ Implementations of Quicksort Methods for Sorting Arrays with Lots of Duplicates

Mikhail Semenov

4.83/5 (32 votes)

31 Aug 2015CPOL16 min read

55.2K

441

Efficient Quicksort methods for sorting arrays with lots of duplicate elements

Download QuickSortTests3.zip

Introduction

This article presents implementation of the Quicksort methods that are most suitable for sorting arrays with a lot of duplicate elements. Recursive implementations, as well as those using a stack and multithreading are provided. Benchmarks are included for 4-core and 2-core processors. Comparison with other sorting methods (Timsort, Heapsort and Mergesort) is given. The code attached has been tested using VC++ 2015 and GCC C++ 5.1.

Background

Since Tony Hoare wrote his article "Quicksort" [1-3], quite a few various Quicksort partitioning algorithms have been proposed. Some of them are not well suited for sorting arrays with duplicates. For example, with a lot of duplicates the Lomuto partitioning [4] can easily run out of stack space. In this article, I will look at the most appropriate, most efficient algorithms for sorting arrays with duplicates.

The task of sorting arrays with lots of duplicates may seem to be artificial and theoretical, but such tasks can be found in the real world: for example, sorting the words from a text. I will be presenting this example. In practice, we may find many problems like that when we use non-unique keys for sorting data: telephone calls (the phone number is the key), car service (the car make is the key), visitors to a museum (the place the visitors are coming from is the key).

Various Partitioning Schemes

I have selected the following three partitioning schemes: Hoare Partitioning, Three-Way Partitioning and Dual-Pivot Partitioning. During the preparation of this article, I investigated other methods (Lomuto Partitioning, Dijkstra Three-Way Partitioning [5] and their modifications). But they require more comparisons than the selected methods.

Hoare Partitioning

This partitioning remains one of the most efficient when it comes to general sorting. Here is a recursive implementation in C++:

typedef std::ptrdiff_t Index;

template <class Iterator, class Comparison = std::less<>>
void HoareQuickSort(Iterator a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= left)
        return;

    auto pivot = a[left + (right - left) / 2];

    Index i = left;
    Index j = right;

    while (i <= j)
    {
        while (compare(a[i], pivot))
            ++i;

        while (compare(pivot, a[j]))
            --j;

        if (i <= j)
        {
            std::swap(a[i++], a[j--]);
        }
    }

    HoareQuickSort(a, a + (j + 1), compare);
    HoareQuickSort(a + i, finish, compare);
}

I will use the Index type throughout the article. You may wish to define is as int, but do not use unsigned or std::size_t, as there are methods where negative values are needed.

Comparison can be submitted as a function or a comparison class. If the comparison object is not supplied, the array will be sorted in ascending order. Here are some examples:

bool gt(double x, double y)
{
    return x > y;
}

struct GT
{
    bool operator()(double x, double y) const
    {
        return x > y;
    }
};

int main()
{
    std::vector<double> a{ -5, 2, 3, 4.5 };
    HoareQuickSort(std::begin(a), std::end(a));
    for (auto&& e : a)
    {
        std::cout << e << " "; // -5 2 3 4.5
    }
    std::cout << std::endl;         

    std::vector<double> x{ -5, 2, 3, 4.5 };
    HoareQuickSort(std::begin(x), std::end(x), gt);
   
    for (auto&& e : x)
    {
        std::cout << e << " "; // 4.5 3 2 -5
    }
    std::cout << std::endl;

    std::vector<double> y{ -15, 20, 3, 4.5 };
    HoareQuickSort(std::begin(y), std::end(y), GT());   

    for (auto&& e : y)
    {
        std::cout << e << " "; // 20 4.5 3 -15
    }
    std::cout << std::endl;
}

Three-Way Partitioning

The partitioning scheme that I am going to discuss here is a slight modification of Bentley-McIlroy partitioning [6, 7], which was modified by Robert Sedgewick [8-10]. The method proposed here has fewer swaps than the original. This target of this partitioning scheme is to produce three partitions:

the elements, which are "less" than the pivot value (strictly-speaking where the compare object returns true);
the elements that are equal to the pivot value (!compare(a[i], pivot) && !compare(pivot,a[i]) is true);
the elements, which are "greater" than the pivot (where the compare function returns false).

But there are various ways of achieving that. In Bentley-McIlroy algorithm, the biginning is similar to Hoare partitioning: two indices move simultaneously from both ends of the array. But, meanwhile, extra comparisons is done and extra partitions are created from the elements that are equal to the pivot value. At first four partitions are created:

some of the elements that are equal to the pivot;
the element that are "less" than the pivot;
the elements that are "greater" than the pivot;
the rest of the elements that are equal to the pivot.

Then partitions 1 and 2 are moved between partitions 2 and 3. You may think that there are losts of swaps and there may be a faster way achieving Three-Way Partitioning. But it appears to be the fastest way. For example, Dijkstra Three-Way Partitioning [5] looks simpler, but requires more comparisons.

Here is a recursive Three-Way Quicksort implementation in C++:

template <class Iterator, class Comparison = std::less<>>
void ThreeWayQuickSort(Iterator a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= 0)
        return;

    Index idx1 = left + (right - left) / 2;   

    auto pivot = a[idx1];

    Index i = left;
    Index j = right;

    Index index1 = left - 1;
    Index index2 = right + 1;

    while (i <= j)
    {
        while (compare(a[i], pivot))
            ++i;

        while (compare(pivot, a[j]))
            --j;

        if (i < j)
        {
            if (compare(pivot, a[i]))
            {
                if (compare(a[j], pivot))
                {
                    std::swap(a[i], a[j]); // a[i] != pivot and a[j] != pivot
                }
                else
                {
                    std::swap(a[i], a[j]);  // a[i] != pivot and a[j] == pivot
                    std::swap(a[++index1], a[i]);
                }
            }
            else if (compare(a[j], pivot)) // a[i] == pivot a[j] != pivot
            {
                std::swap(a[i], a[j]);
                std::swap(a[j], a[--index2]);
            }
            else // a[i] == pivot and a[j] == pivot
            {
                std::swap(a[++index1], a[i]);
                std::swap(a[j], a[--index2]);
            }

            ++i;
            --j;
        }
        else if (i == j)
        {
            j = i - 1;
            i++;
            break;
        }
    }
   
    for (Index k = left; k <= index1; k++)
    {
        std::swap(a[k], a[j--]);       
    }

    for (Index k = right; k >= index2; k--)
    {
        std::swap(a[i++], a[k]);       
    };

    ThreeWayQuickSort(a, a + (j + 1), compare);
    ThreeWayQuickSort(a + i, finish, compare);
}

Dual-Pivot Partitioning

This scheme is similar to the method proposed by Vladimir Yaroslavskiy [11]. I have slighly simplified and modified it. The basic idea is that two pivots are selected and three partitions are created. Here is the main part of modification: there are to approaches depending on whether the pivots are the same or not. If the pivots are different and we order them so that compare(pivot1, pivot2) is true (we say, pivot1 is "less" than pivot2), then the following partitions are created:

the elements that are "less" than or equal to pivot1 (!compare(pivot1,a[i]) is true);
the elements that are between pivot1 and pivot2 (compare(pivot1,a[i]) && compare(a[i],pivot2) is true);
the elements that are "greater" than or equal to pivot2 (!compare(a[i],pivot2) is true).

If the selected pivots are the same, the partitions are slightly different:

the elements that are "less" than pivot1 (compare(a[i],pivot1) is true);
the elements that are equal to pivot1 (and obviously equal to pivot2) (!compare(pivot1,a[i]) && !compare(a[i],pivot1) is true);
the elements that are "greater" than pivot1 (compare(pivot1,a[i]) is true).

If the pivots are equal, obviously the second partition does not have to be sorted.

Here is a recursive Dual-Pivot C++ implementation:

template <class Iterator, class Comparison = std::less<>>
void DualPivotQuickSort(Iterator  a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= left)
    {
        return;
    }

    auto idx1 = left + (right - left) / 3;
    auto idx2 = right - (right - left) / 3;

    std::swap(a[idx1], a[left]);
    std::swap(a[idx2], a[right]);

    if (compare(a[right], a[left]))
    {
        std::swap(a[left], a[right]);
    }

    if (right - left == 1)
    {
        return;
    }

    auto pivot1 = a[left];
    auto pivot2 = a[right];

    if (compare(pivot1, pivot2))
    {
        Index less = left + 1;
        Index greater = right - 1;

        while (!compare(a[greater], pivot2))
        {
            greater--;
        }

        while (!compare(pivot1, a[less]))
        {
            less++;
        }

        Index k = less;
        while (k <= greater)
        {
            if (!compare(pivot1, a[k]))
            {
                std::swap(a[k], a[less++]);
            }
            else if (!compare(a[k], pivot2))
            {
                std::swap(a[k], a[greater--]);
                while (!compare(a[greater], pivot2))
                {
                    greater--;
                }

                if (!compare(pivot1, a[k]))
                {
                    std::swap(a[k], a[less++]);
                }
            }
            k++;
        }

        std::swap(a[less - 1], a[left]);
        std::swap(a[greater + 1], a[right]);

        DualPivotQuickSort(a, a + less - 1, compare);
        DualPivotQuickSort(a + greater + 2, finish, compare);
        DualPivotQuickSort(a + less, a + greater + 1, compare);
    }
    else
    {
        // pivot1 == pivot2
        Index less = left + 1;
        Index greater = right - 1;

        while (compare(pivot1, a[greater]))
        {
            greater--;
        }

        while (compare(a[less], pivot1))
        {
            less++;
        }
       
        Index k = less;
        while (k <= greater)
        {
            if (compare(a[k], pivot1))
            {
                std::swap(a[k], a[less++]);
            }
            else if (compare(pivot1, a[k]))
            {
                std::swap(a[k], a[greater--]);
                while (compare(pivot1, a[greater]))
                {
                    greater--;
                }

                if (compare(a[k], pivot1))
                {
                    std::swap(a[k], a[less++]);
                }
            }
            k++;
        }

        std::swap(a[less - 1], a[left]);
        std::swap(a[greater + 1], a[right]);
       
        DualPivotQuickSort(a, a + less - 1, compare);
        DualPivotQuickSort(a + greater + 2, finish, compare);
    }
}

First Indication of Efficiency: Counting Comparisons and Swaps

In this section I will look at the numbers of comparions and swaps for the selected partitioning methods. It will give a rough indication of the speed of the methods.

I have tested the Quicksort methods on vectors of 10 million random-generated elements with various numbers of distinct elements. The produced number of comparisons is shown in Figure 1. This may be a good indication of speed when the comparisons take much more time than the swaps, as in case of std::vector<std::string>.

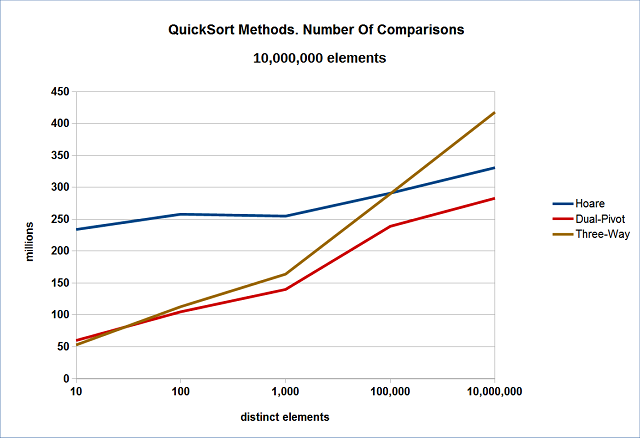
Figure 1. Number of Comparisons

As we can see, Hoare Quicksort is less dependent on the number of distinct elements and is outperformed by the other two methods when there are a lot of duplicates. Three-Way Quicksort is quite good when there are many duplicates, but starts losing its efficiency when the number of duplicates is smaller.

In Figure 2, the numbers of swaps is shown.

Figure 2. Number of Swaps

Three-Way Quicksort has the fewest number of swaps, except in cases when the number of distinct elements is close to 100%.

In Figure 3, I have shown the sum of comparisons and swaps. This may be of good indication of the speed when the comparisons and swaps take approximately the same amount of time, as in case of, for example, std::vector<double>.

Figure 3. Number of Comparisons plus Swaps. Good indication of speed for std::vector<double>

Implementations using a Stack

In order to use a stack, Hoare Partitioning itself can be implemented as follows:

template <class Elem, class Comparison>
struct HoarePartition
{
    ParamList operator()(Elem *a, Index left, Index right, Comparison compare)
    {
        Index i = left;
        Index j = right;
        Elem pivot = a[left+(right-left)/2];

        while (i <= j)
        {
            while (compare(a[i], pivot))
                ++i;

            while (compare(pivot, a[j]))
                --j;

            if (i <= j)
            {
                std::swap(a[i], a[j]);
                ++i;
                --j;
            }
        }

        return { {left,j}, {i, right} };
    }
};

For the other partitioning schemes, the implementations will be similar. The ranges of values are pushed into a ParamList object, where they are ordered in the descending order of range sizes. When the values will be moved from the ParamList object onto the stack, the largest range will be pushed first, which means that, according the LIFO access rule, it will be considered last. This will allow to minimize the size of the stack.

The definition of the related classes is as follows:

struct QuickSortParams
{
    Index m_left;
    Index m_right;
    QuickSortParams():m_left(0),m_right(0) {}
    QuickSortParams(Index left, Index right) :m_left(left), m_right(right) {}

    void setParams(Index left, Index right)
    {
        m_left = left;
        m_right = right;
    }

    void getParams(Index& left, Index& right)
    {
        left = m_left;
        right = m_right;
    }
};

bool CompareParams(const QuickSortParams& p1, const QuickSortParams& p2)
{
    Index d1 = p1.m_right - p1.m_left;
    Index d2 = p2.m_right - p2.m_left;

    if (d1 > d2)
        return true;
    return false;
}

template<class Elem, class Comparison = std::less<Elem>>
void SmallSort(Elem* a, Index left, Index right, Comparison compare = Comparison())
{
    for (Index i = left; i < right; i++)
    {
        for (Index j = i; j >= left && compare(a[j + 1], a[j]); --j)
        {
            std::swap(a[j + 1], a[j]);
        }
    }
};

struct ParamList
{
    std::vector<QuickSortParams> m_vector;
    ParamList() {}

    ParamList(std::initializer_list<QuickSortParams> list) : m_vector(list)
    {
        SmallSort(m_vector.data(), 0, m_vector.size() - 1, CompareParams);
        for (Index i = 0; i < m_vector.size(); i++)
        {
            if (m_vector[i].m_right - m_vector[i].m_left <= 0)
            {
                m_vector.erase(std::begin(m_vector) + i, std::end(m_vector));
                break;
            }
        }
    }

    std::size_t size() const
    {
        return m_vector.size();
    }
   
    QuickSortParams& operator[](std::size_t i)
    {
        return m_vector[i];
    }

    std::vector<QuickSortParams>::iterator begin()
    {
        return m_vector.begin();
    }

    std::vector<QuickSortParams>::iterator end()
    {
        return m_vector.end();
    }
};

Here is the stack implementation:

template <template<class, class> class Method, class Iterator, class Comparison>
void QuickSortRun(Iterator start, Iterator finish, Comparison compare)
{
    Index right = (finish - start) - 1;
    Index left = 0;

    if (right <= 0)
        return;

    typedef typename std::remove_reference<decltype(*start)>::type Elem;
    Elem* a = &*start;

    const Index stackDepth = 64;
    QuickSortParams stack[stackDepth];
    Index stackIndex = -1;

    Method<Elem, Comparison> method;

    while (true)
    {

        if (right - left <= 32)
        {
            SmallSort(a, left, right, compare);
            if (stackIndex != -1)
            {
                stack[stackIndex--].getParams(left, right);
                continue;
            }
            break;
        }

        Index dist = (right - left);
        Index i0 = left;
        Index i1 = left + dist / 3;                    
        Index i2 = left + dist / 2;               
        Index i3 = right - dist / 3;
        Index i4 = right;

        SmallSort(a, { i0,i1,i2,i3,i4 }, compare);       

        ParamList params = method(a, left, right, compare);

        for (auto& p : params)
        {           
            stack[++stackIndex].setParams(p.m_left, p.m_right);        
        }

        if (stackIndex != -1)
        {
            stack[stackIndex--].getParams(left, right);
        }
        else
        {
            break;
        }
    }
}

First of all, if the distance between the first and the last index is less than 32, SmallSort is used, which is based on Insertionsort. Then five elements are selected and ordered using the following, different SmallSort implementation:

template<class Elem, class Comparison = std::less<Elem>>
void SmallSort(Elem* a, std::vector<Index> idx, Comparison compare = Comparison())
{
    Index left = 0;
    Index right = idx.size() - 1;
    for (Index i = left; i < right; i++)
    {
        for (Index j = i; j >= left && compare(a[idx[j + 1]], a[idx[j]]); --j)
        {
            std::swap(a[idx[j + 1]], a[idx[j]]);
        }
    }
}

Then the partitioning method is called, which is provided as a template parameter. The method returns a collection of ranges, which are pushed onto the stack. Then ranges are taken off the stack (if available) and the loop continues until the stack is empty.

Finally, the stack implementation HoareQuickSort will be as follows:

template <class Iterator, class Comparison = std::less<>>
void HoareQuicksort(Iterator start, Iterator finish, Comparison compare = Comparison())
{
   QuickSortRun<HoarePartition>(start, finish,compare); 
}

Multithreading Implementations

The approach is similar to the stack implementation. But instead of pushing values onto the stack, we create threads:

const unsigned SortThreadCount = 7;

template <template<class, class> class Method, class Iterator, class Comparison>
void ParQuickSortRun(Iterator start, Iterator finish, Comparison compare)
{
    Index right = (finish - start) - 1;
    Index left = 0;

    if (right <= 0)
        return;

    typedef typename std::remove_reference<decltype(*start)>::type Elem;
    Elem* a = &*start;

    std::vector<std::thread> threads;

    if ((right-left) < 100000)
    {
        QuickSortRun<Method, Elem*, Comparison>(a + left, a + right + 1, compare);
        return;
    }

    Index range = (right - left) / SortThreadCount;
    
    Method<Elem, Comparison> method;

    while (true)
    {

        if (right - left < range)
        {
            threads.push_back(std::thread(QuickSortRun<Method, Elem*, Comparison>, a + left, a + right + 1, compare));
            break;

        }

        Index dist = (right - left);       
        Index i0 = left;
        Index i1 = left + dist / 3;       
        Index i2 = left + dist / 2;       
        Index i3 = right - dist / 3;       
        Index i4 = right;

        SmallSort(a, { i0,i1,i2,i3,i4 }, compare);

        ParamList params = method(a, left, right, compare);

        bool first = true;

        Index n = params.size();
        for (Index i = n - 1; i >= 0; i--)
        {
            QuickSortParams& p = params[i];
            if (first)
            {
                first = false;
                left = p.m_left;
                right = p.m_right;
            }
            else
            {
                threads.push_back(std::thread(ParQuickSortRun<Method, Iterator, Comparison>, start + p.m_left, start + p.m_right+1, compare));
            }                       
        }

        if (first)
            break;
    }

    for (unsigned i = 0; i < threads.size(); i++)
    {
        threads[i].join();
    }
}

There is the SortThreadCount constant, which I have set to 7. It seems to work well for both 2-core and 4-core processors. But, obviously, for processors with more cores this constant value should be increased. If the distance between the first and the last index is less than 100,000 we don't use multithreading. Then, in the same way as for the stack case, we order the selected 5 elements and call the method. When the list of ranges is returned the last range is used in the current thread, the rest are used for new threads.

The loop continues until either there are no ranges left of the range size is less than the size of the whole array divided by SortThreadCount. In the latter case the non-multithreading method will be used for the last time. After the loop has finished, the ParQuickSortRun function must wait until all the threads have terminated.

Benchmarking

Random-Generated Data

The following tests have been carried out to produce benchmarks:

using stack and multithreaded implementations for the three QuickSort algorithms, as well as using std::sort;
all the tests have been compiled both in VC++2015 and GCC C++ 5.1 for an i7-4790, 4 cores, 3.6 GHz with 8 GB memory;
all the tests have been compiled for GCC C++ 5.1 for an i5-2410, 2 cores, 2.3 GHz, with 6 GB memory;
the three types of arrays have been considered: std::vector<string> (with strings over 71 characters long -- slow on comparison, but fast on swap), std::vector<double> (fast on comparison and swap), std::vector<Block>(where Block is a class, containing a 31-charater array -- slow on both comparison and swap).

Tests for std::vector<Block>

The Block class and the comparison function were defined as follows:

struct Block
{
    static constexpr std::size_t N = 31;
    unsigned char x[N];
    Block(unsigned v = 0)
    {
        for (int i = 0; i < N; i++)
        {
            x[i] = (v >> i) & 1;
        }
    };
};

bool operator<(const Block& a, const Block& b)
{
    for (int i = 0; i < Block::N; i++)
    {
        if (a.x[i] < b.x[i])
            return true;
        if (a.x[i] > b.x[i])
            return false;
    }
    return false;
}

The tests for VC++ on i7-4790 are shown in Figure 4, for GCC C++ on i7-4790 in Figure 5, for GCC C++ on i5-2410 in Figure 6.

Figure 4.

Figure 5.

Figure 6.

I use the word "Par" to name multithreaded implementations. The results show that on average the multithreaded implemetations performed over 3.5 times as fast as their non-multithreaded versions on the 4-core i7 processor, and more than twice as fast on the 2-core i5. Dual-Pivot Quicksort was faster than Hoare QuickSort in all cases. Three-Way Quicksort was faster than Dual-Pivot only in some cases when there were very few distinct elements.

The std::sort on VC++ seems to be similar in peformance to Three-Way Quicksort; and on GCC C++ it is similar to Hoare QuickSort.

Tests for std::vector<std::string>

The sorting of std::vector<std::string> tests for VC++ on i7-4790 are shown in Figure 7, for GCC C++ on i7-4790 in Figure 8, for GCC C++ on i5-2410 in Figure 9.

Figure 7.

Figure 8.

Figure 9.

Here the results are a bit similar to blocks. Dual-Pivot Quicksort was faster than Hoare Quicksort (almost the same when the number of distinct elements was close to the size of the array). Dual-Pivot Quicksort was slightly less efficient than Three-Way Quicksort in some cases when the numbers distict element were less than 1000.

The std::sort performed not as good the corresponding Three-Way on VC++ and Hoare on GCC C++.

Tests for std::vector<double>

The sorting of <font face="Courier New">std::vector<double></font> tests for VC++ on i7-4790 are shown in Figure 10, for GCC C++ on i7-4790 in Figure 11, for GCC C++ on i5-2410 in Figure 12.

Figure 10.

Figure 11.

Figure 12.

Here Dual-Pivot Quicksort beats Hoare Quicksort. Dual-Pivot was slightly slower than Three-Way Quicksort in the mid-range of duplicates (distinct elements in the range between 100 and 100,000). GCC C++ implementation of std::sort was faster than Hoare Quicksort and was faster than single-threaded Dual-Pivot Quicksort. The VC++ std::sort ran slower than single-threaded Three-Way QuickSort.

Comparison with Other Methods

Here I would like to show some comparison with other methods: Timsort [12-15], Heapsort [8] (std::sort_heap) and Mergesort [8]. I will use the following implementation of Mergesort:

template<class Elem, class Comparison>
void merge(Elem *v, Elem* a, Index left, Index right, Index rightEnd, Comparison compare)
{
    Index temp = left, leftEnd = right - 1;
    Index start = left;

    for (Index i = start; i <= rightEnd; i++)
    {
        a[i] = std::move(v[i]);
    }

    while ((left <= leftEnd) && (right <= rightEnd))
    {
        if (compare(a[left], a[right]))
        {
            v[temp++] = std::move(a[left++]);
        }
        else
        {
            v[temp++] = std::move(a[right++]);
        }
    }
    while (left <= leftEnd)
    {
        v[temp++] = std::move(a[left++]);
    }

    while (right <= rightEnd)
    {
        v[temp++] = std::move(a[right++]);
    }
}

template<class Elem, class Comparison>
void mSort(Elem *a, Elem* v, Index left, Index right, Index limit, Comparison compare)
{
    if (left<right)
    {

        if (right - left < 32)
        {
            SmallSort(a, left, right, compare);
            return;
        }

        bool sorted = true;
        for (Index i = left; i < right; i++)
        {
            if (compare(a[i + 1], a[i]))
            {
                sorted = false;
                break;
            }
        }

        if (sorted)
            return;

        // checking for reverse-sorted
        bool reverse_sorted = true;
        for (Index i = left; i < right; i++)
        {
            if (compare(a[i], a[i + 1]))
            {
                reverse_sorted = false;
                break;
            }
        }

        if (reverse_sorted)
        {
            Index i = left;
            Index j = right;
            while (i < j)
            {
                std::swap(a[i++], a[j--]);
            }
            return;
        };

        Index center = (left + right) / 2;
        std::thread th1;
        if (right - left > limit)
        {
            th1 = std::thread(mSort<Elem, Comparison>, a, v, left, center, limit, compare);
            mSort(a, v, center + 1, right, limit, compare);
            th1.join();
        }
        else
        {
            mSort(a, v, left, center, limit, compare);
            mSort(a, v, center + 1, right, limit, compare);
        }
        merge(a, v, left, center + 1, right, compare);
    }
}

template<class Iterator, class Comparison = std::less<>>
void MergeSort(Iterator start, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - start) - 1;

    if (right <= 0)
        return;

    typedef typename std::remove_reference<decltype(*start)>::type Elem;
    Elem* a = &*start;

    Elem *temp = new Elem[right + 1];
    Index limit = (right + 1) / (SortThreadCount*2);
    mSort(a, temp, 0, right, limit, compare);
    auto heap2 = MemoryHeapUsed();
    delete[] temp;
}

The key features are as follows:

The standard move assigment is used for merging, which is efficient for movable objects, such as strings, containers.
Before sorting each fragment is checked whether it is sorted or reverse-sorted: it makes sorting more efficient for oscillating data;
Multithreading is used.

For Timsort, I used the implementation, provided in [14]. I have slighly modified it in the attached zip-file: it has a simpler comparison implementation, which allows it to run slightly faster then the original. I have also added the ability to measure the heap size used by the algorithm. The data for sorting random-generated strings is given in Figure 13.

Figure 13.

Timsort does not have any avantage on random-generated strings. In addition, it used between 479MB and 532MB of extra heap space in these tests. I will discuss Timsort and other methods more in the next section when I will cover the benchmarks for partially-sorted data. Mergesort is not the most efficient, but is performing quite well.

Partially-Sorted Data

In practice, it is often the case that data is correlated or even partially-sorted. I show the tests for partially sorted data of two types:

type 1 - oscillating data (basically a sine curve) shown in Figure 14;
type 2 - oscillating data climbing a slope (similar to sin(x)+x) shown in Figure 15.

Figure 14.

Figure 15.

I have specially tested Timsort on arrays if Big blocks of data, each block containing 1000 bytes. Timsort has an advantage in some tests over other sorting methods as you may see in Figure 16.

Figure 16. Testing Arrays with Partially-Sorted Data Type 1. Each element contains 1000 bytes.

You may see here that Timsort does not perform that well when there are lots of duplicates, but when the number of duplicates decreases its performance dramatically improves. Actually, you may see that Mergesort is very close to Timsort in performance. The reason is that Timsort utilizes the Mergesort algorithm. In these tests the Par Dual-Pivot and Par Three-Way Quicksort methods show the best peformance when there are lots of duplicates. But Timsort is the best when it comes to few duplicates.

Let's us now look and Partially-Sorted Data Type 2. The tests are shown in Figure 17. The "changing slopes" in brackets means how many times the slope changes its direction in the graph: from "ascending" to "descending" or vice versa. If this value is zero, it means that the array is sorted or sorted in the reverse order. In this graph, it means that the vector is sorted in ascending order.

Figure 17. Testing Arrays with Partially-Sorted Data Type 2. In the case of 1,000,000 distinct elements, the data is sorted.

The Timsort performance the best here. It outperforms all the other methods. But this is the case with very few duplicates. When all the elements are sorted Timsort has the best performance as well: 0.54 sec. But here the data elements are big and they take some time to swap.

I have shown that Timsort performs well for vectors of blocks with data Type 1 (oscillating data) with few duplicates. In contrast, when we deal with arrays of strings, where swap operations involve just swapping pointers, Timsort, although performs sometimes better than non-parallel Quicksort methods, does not outperform multithreading Quicksort methods -- Par Hoare, Par Dual-Pivot and Par Three-Way. The results for strings are shown in Figure 18.

Figure 18. Testing Arrays with Partially-Sorted Data Type 1. Each element is of type std::string, which make it easy to swap them.

Here the multithreading Three-Way works slightly better when it comes to sorting lots of duplicates. But Par Dual-Pivot and Par Hoare are better when the number of duplicates decreases. Similar results you may find for the vectors of double floating-point values: the parallel Quicksort methods are the fastest.

A few words about the comparison between Timsort and Quicksort methods:

Heap space: in most tests Timsort allocates extra k*sizeof(elem)*N bytes on the heap (where 0.125 <=k <= 0.5 and N is the size of the array). For example, for 1,000,000 blocks of 1000 bytes this methods used between 121MB and 487MB of the heap. In contrast, Quicksort needs about 1024 bytes for a stack, and does not use any extra heap space.
Timsort is good at sorting big blocks of partially-sorted data, while Quicksort is better at sorting arrays containing containers, simple types and pointers, where the data may be totally random. In practice, Timsort is good for sorting database data.
Quicksort can be easily parallelized: it is more difficult to do it for Timsort. There is no parallel implementation for it yet. My feeling is that when it comes to parallel implementation it probably will need even more heap space. In principle, it is always possible to split array into parts and merge them, but extra heap is needed [16]. Quicksort can be easily parallelized and take advantage of the multicore processors.
For arrays with lots of duplicates, Dual-Pivot Quicksort and Three-Way Quicksort are the fastest methods among the discussed so far.

A Real-world Problem: Extracting Words from a Text and Presenting Them in Alphabetical Order

Here is a practical problem: extracting all the distinct words from a text and sorting them in ascending order. It does not matter how we store the final result (an ordered set or a vector). The results are shown in Figure 19.

The exact problem is this. A vector of all the 1.5 million words from a text, already converted into uppercase is given. The task is to convert it to a collection of distinct words presented in alphabetical order. In this case, the resulting collection will contain 24,355 words. I used a text combined from several books by Alexandre Dumas [17]. I tried texts in other European languages: the results were similar.

Figure 19. Extracting distinct words from a text and sorting them

For example, for Hoare Quicksort I measured the execution time of the following code:

HoareQuicksort(std::begin(words), std::end(words));
auto it = std::unique(words.begin(), words.end());
words.erase(it, words.end());

For std::set the following time was measured:

std::set<std::string> st;
for (auto& x : words)
{
   st.insert(std::move(x));
}

Contrary to what some of the readers may expect, using std::set is not the fastest way. Timsort and Heapsort are the slowest. And multithreading Dual-Pivot and Three-Way Quicksort are the fastest.

Conclusion

Dual-Pivot QuickSort is faster than Hoare in all cases. Three-Way Quicksort may be sligtly faster than Dual-Pivot in some cases with a lot of duplicates, but when the number of duplicates is small (number distinct elements is over 95% of the size of the array) Dual-Pivot is the winner. The average speed increase of multithreaded implementation is roughly propotionate to the number of cores. Since we live in a multi-core processor world, it would be good if multithreaded sorting algorithms were provided in the C++ Standard Library.

Using the Code

All the attached code should be compiled with optimization. For GCC C++, it is recommended to use the following options:

g++ -m64 -Ofast -march=native -funroll-loops -ffast-math -std=c++14 %1.cpp -o %1.exe

For VC++, I would suggest the following options:

In addition, you may consider using the following option:

Enable Enhanced Instruction Set Advanced Vector Extensions 2 (/arch:AVX2)

Major Revisions

31 August 2015. First Version.
06 September 2015. Comparison with Timsort, Mergesort and Heapsort has been added; benchmarks for partially-sorted data.
13 September 2015. The standard Heapsort (a combination of std::make_heap and std::sort_heap) is used in these examples. A different more efficient, implementation of Mergesort is provided. A real-word example is added: extracting distinct words from a text.