• Download GenericCPPLib - 30.4 KB
• Download source from GitHub

Introduction

Usually a standard C/C++11 modules provides quite enough services to accomplish common programming tasks, but sometimes unusual routines are required to reach some specific goals. Here, you will find an example of such functions, which I tried to design in a way in which they can do their job as fast as possible, or at least with the good, decent complexity.

Background

In addition to the C/C++11 <math> module, which provides routines to deal with the individual numbers and C/C++ bitwise operators, which allows to work with the individual bits in integral numbers, the standard C++/C++11 library contains modules with utilities which work with the numbers and bits in ranges: <algorithm>, <numeric> and <bitset> (this one replaces the deprecated vector<bool>). Also, there is one specific C++11 module to work with the proportions (ike 1:3, 1000:1 etc): <ratio>. Some of these modules will be used within my code.

And of course, if you are thinking in bits and looking for some low-level optimization, you should clearly familiarize yourself with this page: Bit Twiddling Hacks.

Some of the subroutines provided below can be (and should be, if possibly) replaced with the compiler-specific intrinsics, like MS VS compiler Intrinsics / GCC compiler Intrinsics and there are also platform-specific Intel intrinsics.

Using Code

From 'MathUtils' class (and module):

Numeric

1) getTenPositiveDegree

Description: Returns 10 in the specified power

Complexity: constant - O(1)

Code

// Up to 10^18; returns zero if degree > 18
static long long int getTenPositiveDegree(const size_t degree = 0U) throw() {
  static const long long int TABLE[] =
     // 32 bit
    {1LL, 10LL, 100LL, 1000LL, 10000LL, 100000LL, 1000000LL, 10000000LL, 100000000LL, 1000000000LL,
     // 64 bit
     10000000000LL, 100000000000LL, 1000000000000LL, 10000000000000LL, 100000000000000LL,
     1000000000000000LL, 10000000000000000LL, 100000000000000000LL, 1000000000000000000LL};
  return degree < (sizeof(TABLE) / sizeof(*TABLE)) ? TABLE[degree] : 0LL; // 0 if too high
}

Of course, the same result can be achieved by using the standard pow routine, but its complexity isn't defined. It could be constant, and could be not.

'std::extent<decltype(TABLE)>::value' can be used to replace the 'sizeof(TABLE) / sizeof(*TABLE)'.

2) getPowerOf2

Description: Returns 2 in the specified power

[!] Use 63 idx. very carefully - ONLY to get the appropriate bit. mask
 (zeroes + sign bit set), BUT NOT the appropriate value (returns negative num.) [!]

Complexity: constant - O(1)

Code

static long long int getPowerOf2(const size_t pow) throw() {
  static const long long int POWERS[] = { // 0 - 62
    1LL, 2LL, 4LL, 8LL, 16LL, 32LL, 64LL, // 8 bit
    128LL, 256LL, 512LL, 1024LL, 2048LL, 4096LL, 8192LL, 16384LL, 32768LL, // 16 bit
    //// 32 bit
    65536LL, 131072LL, 262144LL, 524288LL, 1048576LL, 2097152LL,
    4194304LL, 8388608LL, 16777216LL, 33554432LL,
    67108864LL, 134217728LL, 268435456LL, 536870912LL, 1073741824LL,
    //// 64 bit
    2147483648LL, 4294967296LL, 8589934592LL, 17179869184LL, 34359738368LL, 68719476736LL,
    137438953472LL, 274877906944LL, 549755813888LL, 1099511627776LL, 2199023255552LL,
    4398046511104LL, 8796093022208LL, 17592186044416LL, 35184372088832LL, 70368744177664LL,
    140737488355328LL, 281474976710656LL, 562949953421312LL, 1125899906842624LL, 2251799813685248LL,
    4503599627370496LL, 9007199254740992LL, 18014398509481984LL, 36028797018963968LL,
    72057594037927936LL, 144115188075855872LL, 288230376151711744LL, 576460752303423488LL,
    1152921504606846976LL, 2305843009213693952LL, 4611686018427387904LL,
    -9223372036854775808LL // 63-th bit (sign bit) set bit mask
  };
  return pow >= std::extent<decltype(POWERS)>::value ? 0LL : POWERS[pow];
}

This one can be used if the standard exp2 routine complexity isn't constant for some reason.

3) getDigitOfOrder

Description: Returns the decimal digit of a specified order

Returns 1 for (0, 21), 6 for (1, 360), 2 for (1, 120), 7 for (0, 7), 4 for (1, 40);
        0 for (0, 920) OR (3, 10345) OR (0, 0) OR (4, 10) etc

'allBelowOrderDigitsIsZero' will be true for (0, 7) OR (0, 20) OR (1, 130) OR (2, 12300) OR (0, 0)

Negative numbers are allowed;

order starts from zero (for number 3219 zero order digit is 9)

Complexity: constant - O(1)

Code

static size_t getDigitOfOrder(const size_t order, const long long int num,
                              bool& allBelowOrderDigitsIsZero) throw()
{
  const auto degK = getTenPositiveDegree(order);
  const auto shiftedVal = num / degK; // shifting to the speicified order, ignoring remnant
  allBelowOrderDigitsIsZero = num == (shiftedVal * degK); // shift back without adding remnant
  return static_cast<size_t>(std::abs(shiftedVal % 10LL)); // getting the exact digit
}

4) getArrayOfDigits

Description: Converting number into an array (reversed) of the decimal digits OR into POD C string (based upon the options specified), gathers statistics.

'arraySize' will holds {9, 0, 2, 6, 4, 1} for 902641,
                       {5, 4, 8, 2, 3} for 54823 etc if 'symbols' is false
                       {'9', '0', '2', '6', '4', '1', '\0'} AND
                       {'5', '4', '8', '2', '3', '\0'} otherwise

'count' will hold actual digits count (64 bit numbers can have up to 20 digits)
 i. e. 'count' determines digit's degree (highest nonze-zero order)

Fills buffer in the reversed order (from the end), returns ptr. to the actual str. start

Returns nullptr on ANY error

Negative numbers ok, adds sign. for the negative num. if 'symbols' is true

Can be used as a num-to-str. convertion function (produces correct POD C str. if 'symbols' is true)

'num' will hold the remain digits, if the buffer is too small

Complexity: linear - O(n) in the number degree (log10(num))

Code

static char* getArrayOfDigits(long long int& num, size_t& count,
                              char* arrayPtr, size_t arraySize,
                              size_t (&countByDigit)[10U], // statistics
                              const bool symbols = false) throw()
  {
    count = size_t();
    memset(countByDigit, 0, sizeof(countByDigit));

    if (!arrayPtr || arraySize < 2U) return nullptr;
    arrayPtr += arraySize; // shift to the past-the-end
    if (symbols) {
      *--arrayPtr = '\0'; // placing str. terminator
      --arraySize; // altering remain size
    }
    const bool negative = num < 0LL;
    if (negative) num = -num; // revert ('%' for the negative numbers produces negative results)
    char currDigit;
    
    auto getCurrCharUpdateIfReqAndAdd = [&]() throw() {
      currDigit = num % 10LL;
      num /= 10LL;

      ++countByDigit[currDigit];
      if (symbols) currDigit += '0';
      
      *--arrayPtr = currDigit;
      ++count;
    };
    
    while (true) {
      getCurrCharUpdateIfReqAndAdd(); // do the actual job
      if (!num) break; // that was a last digit
      if (count >= arraySize) return nullptr; // check borders
    }
    if (negative && symbols) {
      if (count >= arraySize) return nullptr; // check borders
      *--arrayPtr = '-'; // place negative sign.
    }
    return arrayPtr;
  }

5) rewindToFirstNoneZeroDigit

Description: (updates an incoming number)

90980000 -> 9098, -1200 -> -12, 46570 -> 4657, -44342 -> -44342, 0 -> 0 etc

Complexity: linear - O(n) in the 1 + trailing zero digits count in a number, up to the number degree (log10(num))

Code

static void rewindToFirstNoneZeroDigit(long long int& num,
                                       size_t& skippedDigitsCount) throw()
{
  skippedDigitsCount = size_t();
  if (!num) return;

  auto currDigit = num % 10LL;
  while (!currDigit) { // while zero digit
    num /= 10LL;
    ++skippedDigitsCount;

    currDigit = num % 10LL;
  }
}

6) getLastNDigitsOfNum

Description: (incoming number is unaltered)

(2, 1234) -> 34; (0, <whatever>) -> 0; (1, -6732) -> 2; (325, 12) -> 12

Complexity: constant - O(1)

Code

template<typename TNumType>
static TNumType getLastNDigitsOfNum(const size_t n, const TNumType num) throw() {
  if (!n || !num) return static_cast<TNumType>(0);

  const auto divider = getTenPositiveDegree(n);
  if (!divider) return num; // if too high 'n'

  auto result = static_cast<TNumType>(num % divider);
  if (result < TNumType()) result = -result; // revert if negative

  return result;
}

7) getFirstNDigitsOfNum

Description: (incoming number is unaltered)

(0, <whatever>) -> 0; (97, 21) -> 21; (56453, 0) -> 0; (3, 546429) -> 546

Complexity: amortised constant ~O(1), based on the log10 complexity

Code

template<typename TNumType>
static TNumType getFirstNDigitsOfNum(const size_t n, const TNumType num) throw() {
  if (!n) return TNumType();

  const auto count = static_cast<size_t>(log10(num)) + 1U;
  if (count <= n) return num;

  return num / static_cast<TNumType>(getTenPositiveDegree(count - n)); // reduce
}

log10 complexity would probably be constant O(1) or log - logarithmic O(log log n).

8) parseNum

Description: parses number using the single divider or an array of dividers

'dividers' is an array of numbers which will be used as a dividers to get the appropriate result,
 which will be placed at the corresponding place in the 'results' array

Func. will stop it work when either 'num' will have NO more data OR zero divider is met
 OR the 'resultsCount' limit is reached

Func. will use either 'divider' OR 'dividers' dependig on the content of this values:
 if 'divider' is NOT zero - it will be used, otherwise i-th value from the 'dividers' will be used
  (if 'dividers' is NOT a nullptr)

Both 'dividers' AND 'results' arrays SHOULD have at least 'resultsCount' size

After return 'resultsCount' will hold an actual elems count in the 'results' array

After return 'num' will hold the rest data which is NOT fitted into the 'results' array

Complexity: linear - O(n), where n is up to 'resultsCount'

Code

static void parseNum(unsigned long long int& num,
                     const size_t divider, const size_t* const dividers,
                     size_t* const results, size_t& resultsCount) throw()
{
  if (!results || !resultsCount) {
    resultsCount = 0U;
    return;
  }
  auto resultIdx = 0U;
  size_t currDivider;

  for (; num && resultIdx < resultsCount; ++resultIdx) {
    currDivider = divider ? divider : (dividers ? dividers[resultIdx] : 0U);
    if (!currDivider) break;

    results[resultIdx] = num % currDivider;
    num /= currDivider;
  }
  resultsCount = resultIdx;
}

This strategy can be used, for example, to parse file size or an I/O operation speed or date-time from the machine format to user-friendly representation. See below.

9) addFormattedDateTimeStr

Description: provides user-friendly representation of the POSIX time, support RU, ENG languages

Date/time str. wil be added (concatenated) to the provided 'str'; returns 'str'

'TStrType' should support '+=' operator on the POD C strs AND chars
 AND 'empty' func. which returns true if the str. IS empty (false otherwise)

Complexity: linear - O(n), up to the 'dividers' count

Code

#pragma warning(disable: 4005)
#ifdef _MSC_VER
  #define _CRT_SECURE_NO_WARNINGS
#endif
#pragma warning(default: 4005)

// Date/time str. wil be added (concatenated) to the provided 'str'; returns 'str'
// 'TStrType' should support '+=' operator on the POD C strs AND chars
//  AND 'empty' func. which returns true if the str. IS empty (false otherwise)
// [!!] Use this to format ONLY the time passed, NOT the actual date/time [!!]
// TO DO: improve RU language support
template<typename TStrType>
static TStrType& addFormattedDateTimeStr(unsigned long long int timeInSecs, TStrType& str,
                                         const bool longPrefixes = true,
                                         const bool eng = true) throw()
{
  static const char* const ENG_LONG_POSTFIXES[] =
    {"seconds", "minutes", "hours", "days", "months", "years", "centuries", "millenniums"};
  static const char* const ENG_SHORT_POSTFIXES[] =
     {"sec", "min", "hr", "d", "mon", "yr", "cen", "mil"};

  static const char* const RU_LONG_POSTFIXES[] =
    {"??????", "?????", "?????", "????", "???????", "???", "?????", "???????????"};
  static const char* const RU_SHORT_POSTFIXES[] =
    {"???", "???", "???", "??", "???", "???", "???", "???"};

  static const auto COUNT = std::extent<decltype(ENG_LONG_POSTFIXES)>::value;

  auto getPostfix = [&](const size_t idx) throw() {
    auto const list = longPrefixes ? (eng ? ENG_LONG_POSTFIXES : RU_LONG_POSTFIXES) // LONG
                                   : (eng ? ENG_SHORT_POSTFIXES : RU_SHORT_POSTFIXES); // SHORT
    return idx < COUNT ? list[idx] : "";
  };

  static const size_t DIVIDERS[] =
  // \/ 60 seconds in the minute    \/ 10 centuries in the millennium
    {60U, 60U, 24U, 30U, 12U, 100U, 10U};
  //                 ^ Month last approximately 29.53 days

  size_t timings[COUNT]; // = {0}
  auto timingsCount = std::extent<decltype(DIVIDERS)>::value;

  if (!timeInSecs) { // zero secs
    *timings = 0U;
    timingsCount = 1U;
  } else parseNum(timeInSecs, 0U, DIVIDERS, timings, timingsCount);

  bool prev = !(str.empty());
  char strBuf[32U];

  if (timeInSecs) { // some data rest (after ALL divisions)
    sprintf(strBuf, "%llu", timeInSecs);

    if (prev) str += ' '; else prev = true;
    str += strBuf;
    str += ' ';
    str += getPostfix(COUNT - 1U);
  }
  for (auto timingIdx = timingsCount - 1U; timingIdx < timingsCount; --timingIdx) {
    if (timings[timingIdx]) { // if NOT zero
      sprintf(strBuf, "%llu", timings[timingIdx]);

      if (prev) str += ' '; else prev = true;
      str += strBuf;
      str += ' ';
      str += getPostfix(timingIdx);
    }
  }
  return str;
}
#ifdef _MSC_VER
  #undef _CRT_SECURE_NO_WARNINGS
#endif

This:

#define _CRT_SECURE_NO_WARNINGS

is MS specific and used because in the MS VS 2013+

sprintf

is deprected.

Bits

1) getBitCount

Description: collects bit statistics (total meaningful; setted count)

Works with the negative numbers (setted sign. bit counts as positive AND meaning: included in 'total')

Complexity: linear - O(n) in setted (ones) bit's count (zero bits - both meaning and not are skipped)

Code

template<typename TNumType>
static void getBitCount(TNumType num, BitCount& count) throw() {
  count.clear();

  if (!num) return;
  if (num < TNumType()) { // if negative
    // Reverse, reset sign bit (to allow Brian Kernighan's trix to work correct)
    num &= std::numeric_limits<decltype(num)>::max();
    ++count.positive; // count sign bit as positive
    ++count.total; // count sign bit as meaning (significant)
  }
  // Determine bit count by the most significant bit set
  count.total = static_cast<size_t>(log2(num)) + 1U;
  do {
    ++count.positive;
    // Brian Kernighan's trix (clear the least significant bit set)
    num &= (num - TNumType(1U));
  } while (num);
}

This function is optimized by skipping zero bits, using

while (num)

condition and Brian Kernighan's trix.

Stats struct

struct BitCount {

    BitCount& operator+=(const BitCount& bitCount) throw() {
      total += bitCount.total;
      positive += bitCount.positive;

      return *this;
    }

    void clear() throw() {
      total = size_t();
      positive = size_t();
    }

    size_t total; // significant ONLY (intermediate zero bits including ofc.)
    size_t positive;
  };

Total bits count in a data type is obviously sizeof(T) * 8, if 'T' is signed integral arithmetic type, then one of them - MSB (Most Significant Bit) is a sign bit.

This schema will help you to understand the concept:

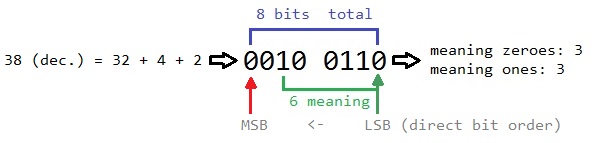
Dec - decimal, LSB - Least Significant Bit.

See also: bit order (it's hardware specific). Below, I'll show you how to detect it (it's very simple).

2) getBitMask

Description: returns bit mask filled with N ones from LSB to MSB (or reverse)

'bitCount' determines how many bits will be set to 1
 (ALL others will be set to 0) AND can NOT be larger then 64

Bits will be filled starting from the least significant
 (by default) OR from most significant (if 'reversedOrder' is true)

Bit masks are often unsigned.

Complexity: constant - O(1)

Code

static unsigned long long int getBitMask(const size_t bitCount,
                                         const bool reversedOrder = false) throw()
{
  static const unsigned long long int MASKS[]
    = {0ULL, 1ULL, 3ULL, 7ULL, 15ULL, 31ULL, 63ULL, 127ULL, 255ULL, 511ULL, 1023ULL,
       2047ULL, 4095ULL, 8191ULL, 16383ULL, 32767ULL, 65535ULL, 131071ULL, 262143ULL,
       524287ULL, 1048575ULL, 2097151ULL, 4194303ULL, 8388607ULL, 16777215ULL, 33554431ULL,
       67108863ULL, 134217727ULL, 268435455ULL, 536870911ULL, 1073741823ULL, 2147483647ULL,
       4294967295ULL, 8589934591ULL, 17179869183ULL, 34359738367ULL, 68719476735ULL,
       137438953471ULL, 274877906943ULL, 549755813887ULL, 1099511627775ULL, 2199023255551ULL,
       4398046511103ULL, 8796093022207ULL, 17592186044415ULL, 35184372088831ULL,
       70368744177663ULL, 140737488355327ULL, 281474976710655ULL, 562949953421311ULL,
       1125899906842623ULL, 2251799813685247ULL, 4503599627370495ULL, 9007199254740991ULL,
       18014398509481983ULL, 36028797018963967ULL, 72057594037927935ULL, 144115188075855871ULL,
       288230376151711743ULL, 576460752303423487ULL, 1152921504606846975ULL, 2305843009213693951ULL,
       4611686018427387903ULL, 9223372036854775807ULL,
       // Last, equal to the 'std::numeric_limits<unsigned long long int>::max()'
       18446744073709551615ULL};
  static const auto COUNT = std::extent<decltype(MASKS)>::value;

  if (bitCount >= COUNT) return MASKS[COUNT - 1U]; // return last
  return reversedOrder ? MASKS[COUNT - 1U] ^ MASKS[COUNT - 1U - bitCount] : MASKS[bitCount];
}

3) setBits

Description

Will set bits with the specified indexes to 1 (OR to 0 if 'SetToZero' is true)

ANY value from the 'idxs' array should NOT be larger then 62

[!] Should work correct with the signed num. types (NOT tested) [!]

Complexity: linear O(n), where n = 'IndexesCount'

Code

template<const bool SetToZero = false, typename TNumType, const size_t IndexesCount>
static void setBits(TNumType& valueToUpdate, const size_t(&idxs)[IndexesCount]) throw() {
  static const size_t MAX_BIT_IDX = std::min(sizeof(valueToUpdate) * 8U - 1U, 62U);

  decltype(0LL) currBitMask;
  for (const auto bitIdx : idxs) {
    if (bitIdx > MAX_BIT_IDX) continue; // skip invalid idxs

    currBitMask = getPowerOf2(bitIdx);
    if (SetToZero) {
      valueToUpdate &= ~currBitMask; // use reversed mask to UNset the specified bit
    } else valueToUpdate |= currBitMask; // set specified bit
  }
}

4) parseByBitsEx

Description: used to parse individual bits, individual bytes, variable count of bits (multiply of 2 OR 8 OR NOT)

Return the last meaning (holding actual data) part INDEX OR -1 if NOT any meaning part is presented

NOT meaning parts (including zero-size AND negative-size parts) will be filled with zeroes

First meaning part will hold the least significant bit(s) AND so on

At the func. end 'num' will hold unprocessed data (if left)
 shifted to the beginning (to the least significant bit)

[!] ANY part size from the 'partSizes' can NOT be higher then
 the actual size in bits of the types 'TNumType' OR 'TPartType' (MAX = 64) [!]

Prefer 'TPartType' AND 'TPartSizeType' to be unsigned integral number types (as so 'TNumType')

[!] If 'num' is a NEGATIVE number, then the sign. bit will be FORCEFULLY RESETED,
 so do NOT use NEGATIVE numbers here [!]

Complexity: linear - O(n), where n = 'PartCount'

Code

template<typename TNumType, class TPartSizeType, class TPartType, const size_t PartCount>
static int parseByBitsEx(TNumType& num, const TPartSizeType (&partSizes)[PartCount],
                         TPartType (&parts)[PartCount]) throw()
{
  auto filledParts = 0U;
  auto lastMeaning = -1; // idx.

  if (num) { // fill meaning parts AND invalid-size parts (if presented)
    auto meaningParts = 0U, incorrectParts = 0U; // counters

    if (num < TNumType()) { // if negative
      //// Reverse, reset sign bit (to allow bitwise right shifting to work correct)
      //// std::remove_reference<decltype(num)>::type == TNumType
      num &= std::numeric_limits<typename std::remove_reference<decltype(num)>::type>::max();
    }
    static const auto MAX_PART_SIZE =
      std::min(sizeof(TNumType) * 8U, sizeof(TPartType) * 8U); // in bits

    TNumType bitMask;
    TPartSizeType currPartSize;
    do {
      currPartSize = partSizes[meaningParts];

      if (currPartSize < TPartSizeType(1U)) { // invalid-size part
        parts[filledParts++] = TPartType(); // zeroize part
        ++incorrectParts;
        continue;
      }
      if (currPartSize > MAX_PART_SIZE) currPartSize = MAX_PART_SIZE; // check & correct

      bitMask = static_cast<TNumType>(getBitMask(currPartSize, false)); // to extract the part

      parts[lastMeaning = filledParts++] = static_cast<TPartType>(num & bitMask);
      ++meaningParts;

      num >>= currPartSize;
    } while (num && filledParts < PartCount);
  }
  while (filledParts < PartCount)
    parts[filledParts++] = TPartType(); // zeroize remaining parts

  return lastMeaning;
}

This one can be used for parsing bit packed (in trivial integral type) data.

For example (assuming direct bit order):

5) getBitStr

Description: returns binary str. representation of the number (bit order in this str. is always direct: MSB <- LSB)

Returns ptr. to the actual beginning of the str.
 (buffer will be filled in the reversed order - from the end)

For the negative numbers sign bit simb. in the str. will be set at its place
 (according to the size of the 'TNumType')
  AND intermediate unmeaning zero bits will be filled -
   BUT ALL of this will happen ONLY if the buf. is large enough

If the provided buf. is too small to hold all the data containing in 'num',
 then 'num' will hold the remaining data
  (INCLUDING sign bit at it's ACTUAL place for the NEGATIVE number) 
   shifted to the beginning (to the LEAST significant bit) after return from the func.

[!] Works with the negative numbers [!]

Complexity

Linear complexity (N = count of the meaning bits in a number,
 up to a sizeof(TNumType) * 8 for negative numbers)

Code

template<typename TNumType>
static char* getBitStr(TNumType& num, char* const strBuf, const size_t strBufSize) throw() {
  if (!strBuf || !strBufSize) return nullptr;

  const auto negative = num < TNumType();
  if (negative)
    num &= std::numeric_limits<TNumType>::max(); // reverse, reset sign bit

  char* const bufLastCharPtr = strBuf + (strBufSize - 1U);
  char* start = bufLastCharPtr; // point to the last smb.
  *start-- = '\0'; // set the str. terminator

  while (num && start >= strBuf) { // reverse fill buf.
    *start-- = '0' + (num & TNumType(1U));
    num >>= 1U;
  }
  if (negative) {
    char* const signBitSymbPtr = bufLastCharPtr - sizeof(TNumType) * 8U;
    // If buffer size is quite enough to hold the sign bit symb.
    if (signBitSymbPtr >= strBuf) {
      while (start > signBitSymbPtr)
        *start-- = '0'; // set unmeaning zero bits between sign AND meaning bits
      *start-- = '1'; // set sign bit symb.
    }
    if (num) // return sign bit ONLY if some data remains
      num |= std::numeric_limits<TNumType>::min();
  }
  return start + 1U;
}

6) ReverseBitsInByteEx

Description: here

Complexity

Effective, uses lookup table (const complexity)

Code

static unsigned char ReverseBitsInByteEx(const unsigned char c) throw() {
  static const unsigned char LOOKUP_TABLE[] = {
    0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0, 0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,
    0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8, 0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8,
    0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4, 0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4,
    0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC, 0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,
    0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2, 0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2,
    0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA, 0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA,
    0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6, 0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6,
    0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE, 0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE,
    0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1, 0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,
    0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9, 0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9,
    0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5, 0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5,
    0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED, 0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD,
    0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3, 0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,
    0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB, 0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB,
    0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7, 0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7,
    0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF, 0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF };
  return LOOKUP_TABLE[c];
}

7) ReverseBits

Description: Same as the previous one, but for the other data types (then unsigned char)

ANY integral num. types

Complexity

linear complexity in sizeof(TIntegralNumType)

Code

template <typename TIntegralNumType,
          typename TIntgeralNumPartType = unsigned char,
          class ReverseBitsInPartFunctor = ReverseBitsInByteExFunctor>
static TIntegralNumType ReverseBits(const TIntegralNumType num) throw() {
  static_assert(1U == sizeof(unsigned char), "'unsigned char' type SHOULD be 1 byte long!");
  // SHOULD fits perfectly
  static_assert(!(sizeof(decltype(num)) % sizeof(TIntgeralNumPartType)),
                "Size of 'num' type SHOULD be even size of 'TIntgeralNumPartType'");
  typedef typename std::remove_const<decltype(num)>::type TMutableNumType;
  union Converter {
    TMutableNumType i;
    // Sizeof(char) is ALWAYS 1U, considering to the CPP standart
    // 'sizeof(decltype(num))' obviously SHOULD be larger then
    //  'sizeof(TIntgeralNumPartType)' OR compile error
    TIntgeralNumPartType c[sizeof(decltype(num)) / sizeof(TIntgeralNumPartType)];
  } resultConverter, originalConverter;
  originalConverter.i = num;
  static const auto COUNT = std::extent<decltype(resultConverter.c)>::value;

  TIntgeralNumPartType currOriginalPart;
  ReverseBitsInPartFunctor bitReversingFunctor;
  //// Reversing algo.: 1) reverse parts 2) reverse bits in parts
  for (size_t partIdx = 0U; partIdx < COUNT; ++partIdx) {
    currOriginalPart =
      originalConverter.c[COUNT - partIdx - 1U]; // reverse the part order
    resultConverter.c[partIdx] =
      bitReversingFunctor(currOriginalPart); // reverse the bit order
  }
  return resultConverter.i;
}

Can be adapted to be used with the modified POD types.

8) BitOrderTester (class)

Description: Determines whether hardware specific bit order is direct or reversed

Complexity: constant - O(1), initializes at the startup (as a static singleton)

class BitOrderTester {

public:

  static const BitOrderTester INSTANCE;

  bool reversedBitOrder = false;

private:

  BitOrderTester() throw() {
    // sizeof(char) SHOULD be ALWAYS 1U, due to the CPP standart
    static_assert(sizeof(char) == 1U, "'char' type is NOT 1 byte large!");
    static_assert(sizeof(int) > sizeof('A'), "Too small 'int' size");

    union Converter {
      int i;
      char c[sizeof(decltype(i))];
    } converter = {0};

    *converter.c = 'A'; // sets zero byte - then test is zero byte LSB OR MSB
    // true if zero byte considered LSB (least significant byte)
    //  => the bit order is left <- right (3-th byte is MSB - most significant byte)
    reversedBitOrder = ('A' == converter.i);
  }

  ~BitOrderTester() = default;

  BitOrderTester(const BitOrderTester&) throw() = delete;
  BitOrderTester(BitOrderTester&&) throw() = delete;
  BitOrderTester& operator=(const BitOrderTester&) throw() = delete;
  BitOrderTester& operator=(BitOrderTester&&) throw() = delete;
};

Logic

C++ misses type-safe exclusive or for the standard bool type.

1) XOR

Description: logic exclusive or (NOT bitwise)

[!] Do NOT confuse this with the std. C++ keyword 'xor'
 (which is an alias for the bitwise operator '^') [!]

Complexity: constant - O(1)

Code

static bool XOR(const bool b1, const bool b2) throw() {
  return (b1 || b2) && !(b1 && b2);
}

Hashing

I personally was also requiring some good POD C string hashing routine, because the standard C++11 std::hash misses it. I found FNV-1a hashing algorithm which is short, simple and produces very low collisons count.

1) getFNV1aHash

Description: Returns 'unique' hash value

'str' SHOULD be a POD C null-terminated str.

Returns zero for an empty str.

Complexity: linear - O(n) in the string length (NOT all hashing algorithms has an O(n) complexity, through)

Code

static size_t getFNV1aHash(const char* str) throw() {
  if (!str || !*str) return size_t();
  static_assert(4U == sizeof(size_t) || 8U == sizeof(size_t),
                "Known primes & offsets for 32 OR 64 bit hashes ONLY");

  //// C++11 OPTIMIZATION HINT: better use 'constexpr' instead of 'const'

  // In the general case, almost any offset_basis will serve so long as it is non - zero
  static const unsigned long long int BASISES[] =
    {2166136261ULL, 14695981039346656037ULL}; // 32 bit, 64 bit
  static const size_t OFFSET_BASIS =
    static_cast<decltype(OFFSET_BASIS)>(BASISES[sizeof(size_t) / 4U - 1U]);

  // Some primes do hash better than other primes for a given integer size
  static const unsigned long long int PRIMES[] =
    {16777619ULL, 1099511628211ULL}; // 32 bit, 64 bit
  static const size_t PRIME =
    static_cast<decltype(OFFSET_BASIS)>(PRIMES[sizeof(size_t) / 4U - 1U]);

  auto hash = OFFSET_BASIS;
  do {
    hash ^= *str++; // xor is performed on the low order octet (8 bits) of hash
    hash *= PRIME;
  } while (*str);

  return hash;
}

As you can see, this version supports ONLY 4 byte AND 8 byte hashes (the most common and useful).

Test Code

For Ideone online compiler:

// <Include the code from TypeHelpers AND MathUtils>

#include <iostream>

int main() {
  for (size_t i = 0U; i < 10U; ++i) {
    assert(MathUtils::getTenPositiveDegree(i) == std::pow(10.0, i));
  }
  for (size_t power = 0U; power < 10U; ++power) {
    assert(std::pow(2.0, power) == MathUtils::getPowerOf2(power));
  }
  auto flag = false;
  auto digit_1_ = MathUtils::getDigitOfOrder(3U, 10345LL, flag);
  assert(!digit_1_);
  assert(!flag);
  ////
  char buf[24U] = {'\0'};;
  auto zeroDigitsCount2 = size_t();
  size_t countByDigit[10U] = {0};
  
  // 123456789
  auto returnPtr = "";
  auto n2 = 123456789LL;
  auto n2_initial_ = n2;
  auto count2 = size_t();
  memset(buf, 0, sizeof(buf));
  memset(countByDigit, 0, sizeof(countByDigit));
  returnPtr = MathUtils::getArrayOfDigits(n2, count2, buf,
                                          std::extent<decltype(buf)>::value,
                                          countByDigit, true);

  const size_t countByDigit_TEST1[] = {0, 1, 1, 1, 1, 1, 1, 1, 1, 1};
  assert(!memcmp(countByDigit, countByDigit_TEST1, sizeof(countByDigit)));
  
  assert(0U == *countByDigit);
  assert(returnPtr >= buf);
  assert(count2 < std::extent<decltype(buf)>::value);
  assert(count2 == strlen(returnPtr));
  assert(atoll(returnPtr) == n2_initial_);
  assert(!n2);
  std::cout << n2_initial_ << " = " << returnPtr << std::endl;
  ////
  auto num3 = 90980000LL;
  auto skippedDigitsCount = 0U;
  MathUtils::rewindToFirstNoneZeroDigit(num3, skippedDigitsCount);
  assert(4U == skippedDigitsCount);
  assert(9098LL == num3);
  ////
  assert(34 == MathUtils::getLastNDigitsOfNum(2U, 1234));
  assert(0L == MathUtils::getLastNDigitsOfNum(0U, 1234L));
  assert(2LL == MathUtils::getLastNDigitsOfNum(1U, -6732LL));
  assert(12 == MathUtils::getLastNDigitsOfNum(325U, 12));
  ////
  assert(0 == MathUtils::getFirstNDigitsOfNum(0U, 6428));
  assert(0 == MathUtils::getFirstNDigitsOfNum(56453U, 0));
  assert(0L == MathUtils::getFirstNDigitsOfNum(0U, 0L));
  assert(0LL == MathUtils::getFirstNDigitsOfNum(97U, 0LL));
  ////
  size_t results_0004[] = {1U, 2U, 3U, 4U, 5U, 6U, 7U, 8U};
  auto resultsCount_0004 = std::extent<decltype(results_0004)>::value;
  auto num_0004 = 343580602368ULL;
  auto num_0004Copy = num_0004;
  MathUtils::parseNum(num_0004, 1024U, nullptr, results_0004, resultsCount_0004);
  assert(!num_0004);
  assert(4U == resultsCount_0004);
  assert(319U == results_0004[3U]);
  
  auto num_0004Copy2 = 0ULL;
  auto k = 1ULL;
  for (auto idx = 0U; idx < resultsCount_0004; ++idx) {
    num_0004Copy2 += results_0004[idx] * k;
    k *= 1024ULL;
  }
  assert(num_0004Copy2 == num_0004Copy);
  ////
  std::string dateTimeStr_001 = "date/time:";
  MathUtils::addFormattedDateTimeStr(1234567890ULL, dateTimeStr_001, false);
  std::cout << 1234567890 << " = " << dateTimeStr_001 << std::endl;
  ////
  MathUtils::BitCount bc;
  // 1100000001010111111110100000000110000100010010000001111010001
  MathUtils::getBitCount(1732477657834652625LL, bc);
  assert(24U == bc.positive);
  assert(61U == bc.total);
  ////
  assert(127 == MathUtils::getBitMask(7, false));
  assert(8388607 == MathUtils::getBitMask(23, false));
  
  auto temp1 = std::pow(2.0, 63.0);
  assert(temp1 == MathUtils::getBitMask(1, true));
  temp1 += std::pow(2.0, 62.0);
  temp1 += std::pow(2.0, 61.0);
  auto temp2 = MathUtils::getBitMask(3, true);
  assert(temp1 == temp2);
  temp1 += std::pow(2.0, 60.0);
  temp1 += std::pow(2.0, 59.0);
  temp1 += std::pow(2.0, 58.0);
  temp1 += std::pow(2.0, 57.0);
  temp2 = MathUtils::getBitMask(7, true);
  assert(temp1 == temp2);
  ////
  auto v_01 = 0ULL, v_02 = 0ULL;
  auto v_01b = 0UL, v_02b = 0UL;
  // 1 + 8 + 256 + 32 768 + 17 592 186 044 416 = 17 592 186 077 449
  const size_t idxs1[] = {0U, 3U, 8U, 15U, 44U};
  MathUtils::setBits(v_01, idxs1);
  v_02 = 0ULL;
  for (double idx : idxs1) {
    v_02 |= static_cast<decltype(v_02)>(std::pow(2.0, idx));
  }
  assert(v_01 == v_02);
  ////
  auto lastMeaningIdx = 0;
  // 0001 0110 0111 0001 1110 0000 0000 1111 1011 0101 1011 0000 0010
  auto num_03 = 394853539863298ULL;
  const size_t partSizes_3[] = {7U, 2U, 16U, 10U, 1U, 19U, 5U}; // 60
  size_t parts_3[std::extent<decltype(partSizes_3)>::value] = {123456789};
  lastMeaningIdx = MathUtils::parseByBitsEx(num_03, partSizes_3, parts_3);
  
  assert(5 == lastMeaningIdx); // total meaning: 6
  assert(!num_03);
  
  assert(    2U == parts_3[0U]); // 0000010
  assert(    2U == parts_3[1U]); // 10
  assert(32173U == parts_3[2U]); // 0111110110101101
  assert(  768U == parts_3[3U]); // 1100000000
  assert(    1U == parts_3[4U]); // 1
  assert( 5745U == parts_3[5U]); // 0000001011001110001
  ////
  char strBuf_003[32U] = {0};
  char* strBufPtr_003 = nullptr;
  // 1111110010101011110111111000001110101011001000010110101100100011
  auto num_006 = -239852398529385693LL;
  auto num_006_copy_ = num_006;
  char strBuf_004[64U + 8U] = {0};
  strBufPtr_003 = MathUtils::getBitStr(num_006, strBuf_004, std::extent<decltype(strBuf_004)>::value);
  assert(!strcmp(strBufPtr_003,
                 "1111110010101011110111111000001110101011001000010110101100100011"));
  assert(!num_006);
  std::cout << num_006_copy_ << " =\n\t" << strBufPtr_003 << std::endl;
  ////
  auto c_23_ = '\0';
  auto res_23_ = MathUtils::ReverseBitsInByte(88U);
  assert(26U == res_23_); // 0101 1000 -> 0001 1010
  assert(26U == MathUtils::ReverseBitsInByteEx(88U));
  c_23_ = 88;
  assert(26 == MathUtils::ReverseBits(c_23_));
  ////
  assert(!MathUtils::XOR(true, true));
  assert(!MathUtils::XOR(false, false));
  assert(MathUtils::XOR(true, false));
  assert(MathUtils::XOR(false, true));
  
  return 0;
}

Output

123456789 = 123456789
1234567890 = date/time: 39 yr 8 mon 8 d 23 hr 31 min 30 sec
-239852398529385693 =
    1111110010101011110111111000001110101011001000010110101100100011

Hash Collision Probability Test Code

I am using HashTester class from the HashUtils module to determine the collision probability.

This class creates fixed length ('BufCapacity' - 1) ASCII POD C strings, calculates their hashes using the provided functor:

currHash = strFunctor(currStr);

and (optionally) stores this hashes into a hash map to find the equal hash values of the different strings (and log them into file, if required).

Test strategy (recursive):

// Generic strategy to test auto. generated char. sequences
//  (used to test hashes, through can be useful elsewhere)
// [!] Will stop if mets zero hash. (AND return false) [!]
template <class TStrFunctor, const size_t BufCapacity>
static bool createAndTestCharSeq(Params<BufCapacity>& params, bool logCollisions = true) throw() {
  static_assert(MIN_CHAR_ < MAX_CHAR_, "Invalid char. sequence");
  static const auto LAST_CHAR_IDX_ = BufCapacity - 1U;

  logCollisions = logCollisions && params.outFile;

  const auto currIdx = params.currLen;
  const auto nextIdx = currIdx + 1U;
  const auto toReserveCount = nextIdx + 1U;
  size_t currHash = 0U;
  std::string currStr;
  decltype(std::make_pair(currHash, std::move(currStr))) currPair;
  decltype(params.map->insert(std::move(currPair))) insertResult;
  TStrFunctor strFunctor;
  auto completenessPercentage = 0U;

  auto tryInsert = [&]() throw() {
    //// Fill pair
    currStr.reserve(toReserveCount);
    currStr = params.strBuf;
    currHash = strFunctor(currStr);

    if (!params.map) return true; // skip other part
    currPair.first = currHash;
    if (logCollisions) currPair.second = currStr; // do NOT move, COPY

    try {
      insertResult = params.map->insert(std::move(currPair));
    } catch (...) {
      return false;
    };

    if (!insertResult.second) { // if NOT inserted (duplicate)
      if (params.stats) ++params.stats->duplicateCount; // if collect stats

      if (logCollisions) {
        auto& dupStr = (*insertResult.first).second;
        (*params.outFile) << currHash << ": '" << currStr << "' == '" << dupStr << "'\n";
        if (!(*params.outFile)) return false;
      }
    }
    return true;
  };

  static_assert(MIN_CHAR_ < MAX_CHAR_, "Invalid char codes");
  double progress;
  for (char currChar = MIN_CHAR_; currChar <= MAX_CHAR_; ++currChar) {
    params.strBuf[currIdx] = currChar;

    if (nextIdx < LAST_CHAR_IDX_) { // prolong seq.
      params.currLen = nextIdx;
      if (!createAndTestCharSeq<TStrFunctor, BufCapacity>(params, logCollisions)) return false;
    } else { // seq. end
      if (!tryInsert()) return false; // saving OR logging failed
      if (!currHash) return false; // force stop (skip other) [OPTIMIZATION]

      if (params.stats) { // if collect stats
        ++params.stats->totalCount;

        if (params.stats->comboCount) { // show progress
          progress =
            static_cast<double>(params.stats->totalCount) / params.stats->comboCount * 100.0;
          completenessPercentage
            = static_cast<decltype(completenessPercentage)>(progress);

          if (completenessPercentage > params.lastCompletenessPercentage &&
              !(completenessPercentage % 10U))
          { // step = 10U
            std::cout << ' ' << completenessPercentage;
            params.lastCompletenessPercentage = completenessPercentage;
          }
        }
      }
    }
  } // 'for currChar' END
  return true;
} // 'createAndTestCharSeqA' END

This class (the complete code of it is in the repository) can be used to test other hashing (and not only) algorithms.

Generated character sequences wil be (assuming they setted to be up to a 3 symols long):

aaa

aab

...

aaz

aba

...

abz

...

azz

...

zzz

(ALL null-terminated)

This behaviour can be changed with the predefined constants:

static const auto MIN_CHAR_ = 'a';
static const auto MAX_CHAR_ = 'z'; // 'a'-'z': 26
static const auto ALPHABET_LEN_ = MAX_CHAR_ - MIN_CHAR_ + 1U;

An alphabet length along with the sequence length is defining the resulting sequence array size, which will be a^n (a in the power of n), so both parameters increase dramatically affects the combinations count and, of course, test execution time.

Test example in the Ideone online compiler:

// <Include the hashing routine from MathUtils AND HashTester header>

template <class TStrType>
struct FNV1aHashFunctor {
  auto operator()(const TStrType& str) throw() -> decltype(MathUtils::getFNV1aHash(str.c_str())) {
    return MathUtils::getFNV1aHash(str.c_str());
  }
};

template <class TStrType>
struct STLHashFunctor {
  auto operator()(const TStrType& str) throw() -> decltype(std::hash<std::string>()(str)) {
    return std::hash<std::string>()(str);
  }
};

int main() {
  bool error = false;
    const auto FNV1aHashCollisionProbability_
      = HashTester::getCollisionProbability<FNV1aHashFunctor<std::string>>(error, false);
    std::cout << std::endl << "FNV1a Collision Probability: "
              << FNV1aHashCollisionProbability_ << ", error: " << error << std::endl;
    
    // 'std::hash<std::string>' can be used directly
    error = false;
    const auto STLHashCollisionProbability_
      = HashTester::getCollisionProbability<STLHashFunctor<std::string>>(error, false);
    std::cout << std::endl << "STL Collision Probability: "
              << STLHashCollisionProbability_ << ", error: " << error << std::endl;
  return 0;
}

This test uses default (3) char. sequence length. On this length, I see NO collisions:

10 20 30 40 50 60 70 80 90 100

FNV1a Collision Probability: 0, error: 0

10 20 30 40 50 60 70 80 90 100

STL Collision Probability: 0, error: 0

A very low collision percent can be seen with the char. sequence of 5 symbols:

Points of Interest

Class using TypeHelpers module.

This module is just a small part of the library, which uses C++11 features and which I am working under now, I decided to make it a public property.

Library modules & technologies reference:

• Execute Member Function If It Is Present
• Generate a Parameterized Random Char Sequence
• Generic Random Access Iterator

History

• Update 1: Added link to the MS VS compiler Intrinsics (thanks feanorgem)

• Update 2: More intrinsics (another thanks to feanorgem)