Introduction
Anyone who has ever seen a sine wave and/or a cosine wave will have noticed that both of the curvilinear graphs are drawn on a Cartesian Coordinate (world) system. The origin (0,0) lies in the middle of the graph, as the graphs have a period of 2PI or a width of –PI to +PI. Unlike that system, however, is the X and Y coordinate system of the console terminal: the origin (0,0) resides at the upper left hand corner, which on many older terminals is the location of the VGA buffer. For 2D graphics, the WPF coordinate system locates the origin in the upper-left corner of the rendering area. In the 2D space, the positive X-axis points to the right, and the positive Y-axis points to downward. All coordinates and sizes in the default WPF system are measured in units of 96 dots per inch (DPI), called device-independent pixels. In this system, you can create adaptive layouts to deal with different resolutions, making sure your controls and graphics objects stretch accordingly when the window is stretched. So how would code ensure that we can draw a sine wave and/or a cosine wave?
A key step to creating this line chart is that the original data points in the world coordinate system need to be transformed into points in the units of device independent pixels. Therefore we must write a method that converts points with any unit in the world coordinate system into points with a unit of device-independent pixel in the device coordinate system. So how would the code look? It would have a method accessed in a code-behind file that compiles as a DLL. We'll call the method CurvePoint, and note its access modifiers as private and static:
using System;
using System.Collections.Generic;
using System.Text;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Data;
using System.Windows.Documents;
using System.Windows.Input;
using System.Windows.Media;
using System.Windows.Media.Imaging;
using System.Windows.Shapes;
namespace MyProject
{
public partial class SimpleLineChart : Window
{
private double xmin = 0;
private double xmax = 6.5;
private double ymin = -1.1;
private double ymax = 1.1;
private Polyline pl;
public SimpleLineChart()
{
InitializeComponent();
AddChart();
}
private void AddChart()
{
pl = new Polyline();
pl.Stroke = Brushes.Black;
for (int i = 0; i < 70; i++)
{
double x = i/5.0;
double y = Math.Sin(x);
pl.Points.Add(CurvePoint(
new Point(x, y)));
}
chartCanvas.Children.Add(pl);
pl = new Polyline();
pl.Stroke = Brushes.Black;
pl.StrokeDashArray = new DoubleCollection(
new double[] { 4, 3 });
for (int i = 0; i < 70; i++)
{
double x = i / 5.0;
double y = Math.Cos(x);
pl.Points.Add(CurvePoint(
new Point(x, y)));
}
chartCanvas.Children.Add(pl);
}
private Point CurvePoint(Point pt)
{
Point result = new Point();
result.X = (pt.X - xmin) * chartCanvas.Width / (xmax - xmin);
result.Y = chartCanvas.Height - (pt.Y - ymin) * chartCanvas.Height
/ (ymax - ymin);
return result;
}
}
}
Here is how the application looks when built using Expression Blend 4:
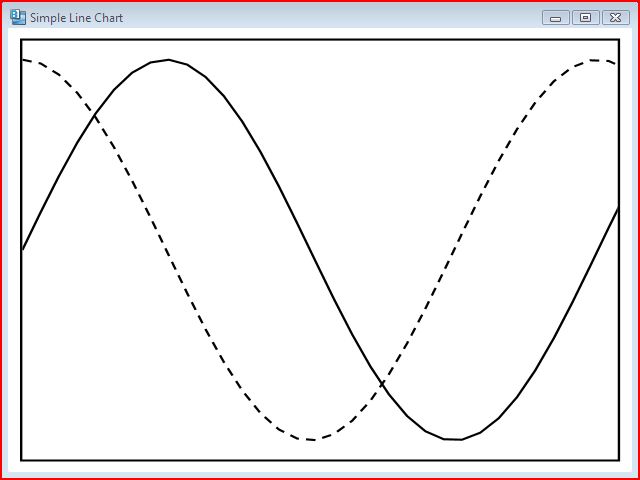
Admittedly, this drawing does not have enough any meaning to one who doesn't have a need for Trigonometry, but it does show how code can work in WPF to create objects without a lot of XAML.
Where is the XAML
The XAML is simple enough:
<Window
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
x:Class="MyProject.SimpleLineChart"
Title="Simple Line Chart"
Width="640" Height="480">
<Viewbox Stretch="Fill">
<Border BorderBrush="Black" BorderThickness="1" Margin="5">
<Canvas Name="chartCanvas"
Width="250" Height="200" ClipToBounds="True"/>
</Border>
</Viewbox>
</Window>
This article has been referenced from the work of Jack Xu.
History
- 26th August, 2010: Initial post
