In this article, I introduce you to an updated version of Kanasz Robert's "Sort Comparison" project.
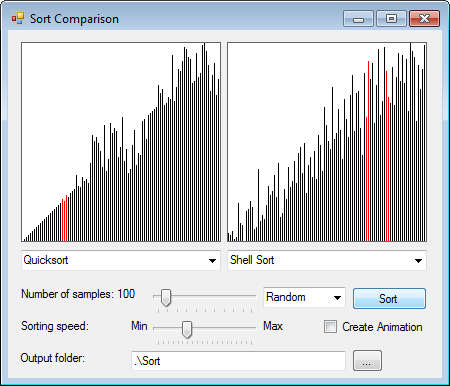
Table Of Contents
This is an update to the excellent work of Kanasz Robert, in which he presented a project which visualizes and compares sorting algorithms. It also contains the NGIF project, which can be used to save these visualizations as GIF files. This program allows the user to choose two of many sorting algorithms and compare them visually, with varying sizes and types of data sets and at varying speeds. It also allows the user to create GIF files of the visualizations.
Mr. Robert did a great job of explaining how many sorting algorithms work, so please see his article for that.
In this version, Bucket Sort was removed because the code functionally matched Pigeonhole Sort. Also, "Quicksort with Bubble Sort" was changed to "Quicksort with Insertion Sort" because Insertion Sort performs better than Bubble Sort. Five algorithms were added: Counting Sort, Merge Sort (Double Storage), Radix Sort, Smoothsort, and Timsort.

Counting Sort, similar to Pigeonhole Sort, is a sorting algorithm which is not a comparison sort, so it uses about 2n comparisons (for finding the minimum and maximum in the first pass) when sorting the data. This allows it to be extremely fast, with its drawbacks being that the data needs to be integers and the range needs to be small. It works by going through the data the first time, finding the minimum and maximum to determine the range. Then it creates a new array with that range and goes through the data again, counting how many of each element it finds. Finally, it goes through this new array and writes the data, sorted, to the original array. Admittedly, some code for this sort was already in the project, it just didn't make it into Mr. Robert's original article.
public IList CountingSort(IList arrayToSort)
{
object min = null;
object max = null;
SetItem(arrayToSort, ref min, 0);
SetItem(arrayToSort, ref max, 0);
for (int i = 1; i < arrayToSort.Count; i++)
{
if (CompareItems(arrayToSort, i, min) < 0)
{
SetItem(arrayToSort, ref min, i);
}
else if (CompareItems(arrayToSort, i, max) > 0)
{
SetItem(arrayToSort, ref max, i);
}
}
int range = (int)max - (int)min + 1;
int[] count = new int[range];
for (int i = 0; i < range; i++)
{
count[i] = 0;
}
for (int i = 0; i < arrayToSort.Count; i++)
{
count[(int)GetItem(arrayToSort, i) - (int)min]++;
}
int z = 0;
for (int i = 0; i < count.Length; i++)
{
while (count[i] > 0)
{
SetItem(arrayToSort, z, (object)(i + (int)min));
z++;
count[i]--;
}
}
return arrayToSort;
}
| Worst case performance: | O(n) |
| Best case performance: | O(n) |
| Average case performance: | O(n) |
| Worst case space complexity: | max(N) - min(N) auxiliary |

Merge Sort is a sorting algorithm which uses a divide-and-conquer recursion to sort small partitions and then combine those partitions into larger ones. The Double Storage version outperforms the In Place version significantly, but uses much more space to do so. It is very fast and competes with Quicksort in speed. When it divides the data down to partitions of size 1 or 0, it can stop recursing because the data of that size is sorted. It then combines the data of two partitions by comparing the first elements of the partitions and writing the smaller element to a new List. Once one of the partitions has been traversed, it can copy the rest of the other partition to the List and return the List as a sorted copy of that range of data, to be merged at the next level up.
public IList MergeSortDoubleStorage(IList a, int low, int high)
{
int l = low;
int h = high;
IList r = new ArrayList();
if (l == h)
{
r.Add(GetItem(a, low));
return r;
}
else if (l > h)
{
return r;
}
int mid = (l + h) / 2;
IList firstList = MergeSortDoubleStorage(a, l, mid);
IList secondList = MergeSortDoubleStorage(a, mid + 1, h);
int startFirst = 0;
int startSecond = 0;
int i = l;
while (startFirst < firstList.Count && startSecond < secondList.Count && i <= h)
{
operationCount++;
if (((IComparable)firstList[startFirst]).CompareTo(secondList[startSecond]) < 0)
{
r.Add(firstList[startFirst]);
SetItem(a, i, firstList[startFirst]);
startFirst++;
i++;
}
else
{
r.Add(secondList[startSecond]);
SetItem(a, i, secondList[startSecond]);
startSecond++;
i++;
}
}
while (startFirst < firstList.Count && i <= h)
{
r.Add(firstList[startFirst]);
SetItem(a, i, firstList[startFirst]);
startFirst++;
i++;
}
while (startSecond < secondList.Count && i <= h)
{
r.Add(secondList[startSecond]);
SetItem(a, i, secondList[startSecond]);
startSecond++;
i++;
}
return r;
}
| Worst case performance: | O(n log n) |
| Best case performance: | O(n log n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: | O(n) auxiliary |

Radix Sort is a non-comparitive integer sorting algorithm which works very fast and can even beat Quicksort. Its main drawback is that it only compares positive integers, although there are versions of it which allow for negative numbers and others for floating point data. It works by copying/moving the the data into specific buckets, based on the value of its least significant bits or digits. It then copies/moves the data back into the original array and iterates again, looking at the next least significant bits or digits. The number of buckets used depends on the number of bits considered in each iteration. If it looks at 8 bits at a time, it uses 256 buckets, one for each combination of 8 0's and 1's.
public IList RadixSort(IList array)
{
int shift = 0;
int totalBits = 32;
int maskLength = 8;
int mask = 255;
List<Queue<int>> buckets = new List<Queue<int>>();
for (int i = 0; i <= mask; i++)
{
Queue<int> q = new Queue<int>();
buckets.Add(q);
}
while (shift < totalBits)
{
int i;
for (i = 0; i < array.Count; i++)
{
int bucketNumber = ((int)GetItem(array, i) >> shift) & mask;
buckets[bucketNumber].Enqueue((int)GetItem(array, i));
}
i = 0;
foreach (Queue<int> bucket in buckets)
{
while (bucket.Count > 0)
{
SetItem(array, i, (object)bucket.Dequeue());
i++;
}
}
shift += maskLength;
}
return array;
}
| Worst case performance: | O(n) |
| Best case performance: | O(n) |
| Average case performance: | O(n) |
| Worst case space complexity: | O(n) auxiliary |

Smoothsort is a version of Heapsort which adapts better to data which is sorted or nearly sorted. Like Heapsort, it builds a heap from the data and then moves the largest item to the end and fixes the heap. A heap is a binary tree where each parent is larger than both of its two children. It works quickly because a heap can be built and fixed quickly. The difference is in how the heap is built within the array. It's more complicated than I dare to understand, but you can find more information in the Wikipedia article and another CodeProject article, "Fastest In-Place Stable Sort", which is where the code is ported from.
The code is about 560 lines, so please download the project to see it.
| Worst case performance: | O(n log n) |
| Best case performance: | O(n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: | O(1) auxiliary |

Timsort is a hybrid sorting algorithm, derived from Merge Sort and Insertion Sort. It's so fast that it's used in Java, Python, and Android. It's designed to work well with real-world data, which tends to have runs of ascending or descending data in it. It works by finding these runs, creating runs (sorting) where there aren't runs, and merging them together. It is also more complicated than I dare to understand, but you can find more information in the Wikipedia article and this code, which I used to create my own version. My code usually works, but it's definitely bugged, so if you can debug it, please let me know.
The code is about 826 lines, so please download the project to see it.
| Worst case performance: | O(n log n) |
| Best case performance: | O(n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: | O(n) auxiliary |
Also useful to know is how different algorithms perform on different types of data sets. For example, Bubble Sort, which is known for its poor performance, does better than Quicksort on sorted data. This is not to say Bubble Sort should be used, it's just an interesting fact, clearly shown in a visualization.
 |  |
| Bubble Sort | Quicksort |
These other types of data sets can also be used to look for worst cases for some sorts, which may cause you to choose not to use the algorithm. For example, let's look at each type of data and compare Quicksort with Timsort, two widely used algorithms.
| Random |
 |  |
| Quicksort | Timsort |
| Reversed |
 |  |
| Quicksort | Timsort |
| Sorted |
 |  |
| Quicksort | Timsort |
| Nearly Sorted |
 |  |
| Quicksort | Timsort |
| Few Unique |
 |  |
| Quicksort | Timsort |
As you can see in these comparisons, they are both very competitive, with Timsort having the advantage in sorting Sorted data. Still, I'm partial to Quicksort because of its relative simplicity and smaller space requirements.
To provide these types of data sets, I just added a combo box and this code:
array1 = new ArrayList(tbSamples.Value);
array2 = new ArrayList(tbSamples.Value);
for (int i = 0; i < array1.Capacity; i++)
{
int y = (int)((double)(i + 1) / array1.Capacity * pnlSort1.Height);
array1.Add(y);
}
for (int i = array1.Count - 1; i > 0; i--)
{
int swapIndex = rand.Next(i + 1);
if (swapIndex != i)
{
object tmp = array1[swapIndex];
array1[swapIndex] = array1[i];
array1[i] = tmp;
}
}
array2 = (ArrayList)array1.Clone();
if (ddTypeOfData.SelectedItem.ToString() == "Random")
{
}
else if (ddTypeOfData.SelectedItem.ToString() == "Sorted")
{
array1.Sort();
array2 = (ArrayList)array1.Clone();
}
else if (ddTypeOfData.SelectedItem.ToString() == "Nearly Sorted")
{
array1.Sort();
int maxValue = array1.Count / 10;
int itemsToMove = rand.Next(1, maxValue);
for (int i = 0; i < itemsToMove; i++)
{
int a = rand.Next(0, array1.Count);
int b = rand.Next(0, array1.Count);
while (a == b)
{
a = rand.Next(0, array1.Count);
b = rand.Next(0, array1.Count);
}
object temp = array1[a];
array1[a] = array1[b];
array1[b] = temp;
}
array2 = (ArrayList)array1.Clone();
}
else if (ddTypeOfData.SelectedItem.ToString() == "Reversed")
{
array1.Sort();
array1.Reverse();
array2 = (ArrayList)array1.Clone();
}
else if (ddTypeOfData.SelectedItem.ToString() == "Few Unique")
{
int maxValue = 10;
if (array1.Count < 100)
maxValue = 6;
maxValue = rand.Next(2, maxValue);
ArrayList temp = new ArrayList();
for (int i = 0; i < maxValue; i++)
{
int y = (int)((double)(i + 1) / maxValue * pnlSort1.Height);
temp.Add(y);
}
for (int i = 0; i < array1.Count; i++)
{
array1[i] = temp[rand.Next(0, maxValue)];
}
array2 = (ArrayList)array1.Clone();
}
Mr. Robert did a great job of setting up a way to visualize the sorting algorithms, but as I worked with the code, I eventually decided to overhaul how it worked. The first change was to highlight in red the action taking place on the data, whether that's a comparison or a change in the data. Second, I made the drawing procedure draw rectangles instead of lines if there was room them, so that the data was more pleasing to the eye. Next, rather than having a system which does an operation, then waits for a specific period of time, I set it up so that it would do a specific number of operations per second, with new images drawn about 25 times per second. This allowed for larger data sets and faster visualizations. I also modified the code to allow different sizes of visualizations, so that the user can maximize the window to get a better view of the data and the action on that data.
Putting all of these together, we add/modify this code in the SortAlgorithm class:
int operationsPerFrame;
int frameMS;
int operationCount;
Dictionary<int, bool> highlightedIndexes = new Dictionary<int, bool>();
DateTime nextFrameTime;
int originalPanelHeight;
public SortAlgorithm(ArrayList list, PictureBox pic, bool sp, string of, int s, string outFile)
{
imgCount = 0;
arrayToSort = list;
pnlSamples = pic;
savePicture = sp;
outputFolder = of;
outputFile = outFile;
operationCount = 0;
operationsPerFrame = s;
frameMS = 1000;
while (frameMS >= 40 && operationsPerFrame > 1)
{
operationsPerFrame = operationsPerFrame / 2;
frameMS = frameMS / 2;
}
bmpsave = new Bitmap(pnlSamples.Width, pnlSamples.Height);
g = Graphics.FromImage(bmpsave);
originalPanelHeight = pnlSamples.Height;
pnlSamples.Image = bmpsave;
nextFrameTime = DateTime.UtcNow;
checkForFrame();
}
private void checkForFrame()
{
if (operationCount >= operationsPerFrame || nextFrameTime <= DateTime.UtcNow)
{
DrawSamples();
RefreshPanel(pnlSamples);
if (savePicture)
SavePicture();
highlightedIndexes.Clear();
operationCount -= operationsPerFrame;
if (DateTime.UtcNow < nextFrameTime)
{
Thread.Sleep((int)((nextFrameTime - DateTime.UtcNow).TotalMilliseconds));
}
nextFrameTime = nextFrameTime.AddMilliseconds(frameMS);
}
}
public void finishDrawing()
{
if (highlightedIndexes.Count > 0)
{
nextFrameTime = DateTime.UtcNow;
checkForFrame();
}
nextFrameTime = DateTime.UtcNow;
checkForFrame();
}
public void DrawSamples()
{
double multiplyHeight = 1;
if (bmpsave.Width != pnlSamples.Width || bmpsave.Height != pnlSamples.Height)
{
bmpsave = new Bitmap(pnlSamples.Width, pnlSamples.Height);
g = Graphics.FromImage(bmpsave);
pnlSamples.Image = bmpsave;
}
if (pnlSamples.Height != originalPanelHeight)
{
multiplyHeight = (double)(pnlSamples.Height) / (double)(originalPanelHeight);
}
g.Clear(Color.White);
Pen pen = new Pen(Color.Black);
SolidBrush b = new SolidBrush(Color.Black);
Pen redPen = new Pen(Color.Red);
SolidBrush redBrush = new SolidBrush(Color.Red);
int w = (pnlSamples.Width / arrayToSort.Count) - 1;
for (int i = 0; i < this.arrayToSort.Count; i++)
{
int x = (int)(((double)pnlSamples.Width / arrayToSort.Count) * i);
int itemHeight = (int)Math.Round(Convert.ToDouble(arrayToSort[i]) * multiplyHeight);
if (highlightedIndexes.ContainsKey(i))
{
if (w <= 1)
{
g.DrawLine(redPen, new Point(x, pnlSamples.Height), new Point(x, (int)(pnlSamples.Height - itemHeight)));
}
else
{
g.FillRectangle(redBrush, x, pnlSamples.Height - itemHeight, w, pnlSamples.Height);
}
}
else
{
if (w <= 1)
{
g.DrawLine(pen, new Point(x, pnlSamples.Height), new Point(x, (int)(pnlSamples.Height - itemHeight)));
}
else
{
g.FillRectangle(b, x, pnlSamples.Height - itemHeight, w, pnlSamples.Height);
}
}
}
}
In order to make new sorting algorithms easier to add, easier to read, and easier to illustrate, I created the functions needed for illustrating any compare, swap, set, or get. These added the appropriate number of operations and called checkForFrame() to draw a new image if necessary.
private object GetItem(IList arrayToSort, int index)
{
if (!highlightedIndexes.ContainsKey(index))
highlightedIndexes.Add(index, false);
operationCount++;
checkForFrame();
return arrayToSort[index];
}
private void SetItem(IList arrayToSort, int toIndex, int fromIndex)
{
arrayToSort[toIndex] = arrayToSort[fromIndex];
if (!highlightedIndexes.ContainsKey(toIndex))
highlightedIndexes.Add(toIndex, false);
operationCount++;
checkForFrame();
}
private void SetItem(IList arrayToSort, int toIndex, object fromObject)
{
arrayToSort[toIndex] = fromObject;
if (!highlightedIndexes.ContainsKey(toIndex))
highlightedIndexes.Add(toIndex, false);
operationCount++;
checkForFrame();
}
private void SetItem(IList arrayToSort, ref object toObject, int fromIndex)
{
toObject = arrayToSort[fromIndex];
if (!highlightedIndexes.ContainsKey(fromIndex))
highlightedIndexes.Add(fromIndex, false);
operationCount++;
checkForFrame();
}
private void SwapItems(IList arrayToSort, int index1, int index2)
{
object temp = arrayToSort[index1];
arrayToSort[index1] = arrayToSort[index2];
arrayToSort[index2] = temp;
if (!highlightedIndexes.ContainsKey(index1))
highlightedIndexes.Add(index1, false);
if (!highlightedIndexes.ContainsKey(index2))
highlightedIndexes.Add(index2, false);
operationCount += 2;
checkForFrame();
}
private int CompareItems(IList arrayToSort, int index1, int index2)
{
if (!highlightedIndexes.ContainsKey(index1))
highlightedIndexes.Add(index1, false);
if (!highlightedIndexes.ContainsKey(index2))
highlightedIndexes.Add(index2, false);
operationCount++;
checkForFrame();
return ((IComparable)arrayToSort[index1]).CompareTo(arrayToSort[index2]);
}
private int CompareItems(IList arrayToSort, int index1, object o)
{
if (!highlightedIndexes.ContainsKey(index1))
highlightedIndexes.Add(index1, false);
operationCount++;
checkForFrame();
return ((IComparable)arrayToSort[index1]).CompareTo(o);
}
private int CompareItems(IList arrayToSort, object o, int index1)
{
if (!highlightedIndexes.ContainsKey(index1))
highlightedIndexes.Add(index1, false);
operationCount++;
checkForFrame();
return ((IComparable)o).CompareTo(arrayToSort[index1]);
}
I became interested in this project after seeing visualizations of sorting algorithms on YouTube and at http://www.sorting-algorithms.com/. In parallel to this, I also have a project which, rather than drawing images, instead sorts, counts operations, and is a timer for the algorithms as they race to sort the data. I was surprised to learn that, after implementing every version of Quicksort I could find, nothing improves (much) on this basic version. The tri-median method does about the same. And the 3-partition version seems to be solving a problem that doesn't really exist. Quicksort does Few Unique types of data faster than Random types of data, so it's not really an issue. I did change the pivot to be random so that it won't come across some worst case set of data and end up with an n2 sorting time. So here's that beautiful, simple function.
public IList Quicksort(IList a, int left, int right)
{
int i = left;
int j = right;
object x = null;
SetItem(a, ref x, rand.Next(left, right + 1));
while (i <= j)
{
while (CompareItems(a, i, x) < 0)
{
i++;
}
while (CompareItems(a, x, j) < 0)
{
j--;
}
if (i < j)
{
SwapItems(a, i, j);
i++;
j--;
}
else if (i == j)
{
i++;
j--;
}
}
if (left < j)
{
Quicksort(a, left, j);
}
if (i < right)
{
Quicksort(a, i, right);
}
return a;
}
Also of interest to me was the sorting algorithm Shellsort, which is such a simple concept to understand and performs nearly as well as Quicksort when you've only got 1000 items or less to sort.
 |  |
| Quicksort | Shellsort |
Some visualizations were surprisingly interesting. For example, watch Bidirectional Bubble Sort actually appear to be a shrinking bubble. Note that this is a very slow sort shown at a high speed.
 |
| Bidirectional Bubble Sort |
Odd-Even Sort looks just like Bubble Sort, which is a data set moving to the right, except that it's two data sets, with one (too large items) moving right and the other (too small items) moving left.
 |  |
| Bubble Sort | Odd-Even Sort |
And finally, Radix Sort's data starts to have a distinct look if you use a wide enough set of data and/or a small enough number of bits/buckets. This is the 8-bit version working on data ranging from 1 to int.MaxValue. The normal version of this program does not allow such a range, in order to accomodate Pigeonhole Sort and Counting Sort.
 |
| Radix Sort |
3/30/2016 - Initial version
