Introduction
This is implementation of the algorithm presented in the paper [Carrasco and Forcada 2002]1, that, in its turn, is founded on the work [Daciuk et al. 2000]2. They described the method for modifying of minimal deterministic finite automaton through adding (or removing) a string into the language accepting by this automaton. The algorithm is given in pseudo-code, and wouldn't be difficult to implement it in any imperative language. But it seemed more interesting to write working realization in functional language, such as F#, that is positioned as a powerful tool for language oriented programming and writing parsers3, so the code may find some use in this areas.
Background
A deterministic finite automaton (DFA) M is a tuple (Q, Σ, δ, q0, F), where:4
- Q is a finite set of states
- Σ is a finite set of input symbols
- δ: Q × Σ → Q is a transition function
- q0 ∈ Q is an initial or start state
- F ⊆ Q is a set of final or accepting states
Automaton M accepts string ω = a1...an ∈ Σ* if M starts in initial state q0, for each ai moves to next state according to δ, and finally stays in one of the accepting states from F. Each automaton M recognizes some regular language L(M), that means all ω ⊆ L(M) are accepted by M. For example, the automaton
-
Q = {0, 1, 2, 3, 4, 5},
-
Σ = {a, b, r},
-
δ is
|
| 0
| 1
| 2
| 3
| 4
| 5
|
| a
| -
| 2
| -
| -
| 5
| -
|
| b
| 1
| -
| 4
| -
| -
| 4
|
| r
| -
| -
| 3
| -
| -
| -
|
-
q0 = 0,
-
F = {2, 3, 5}
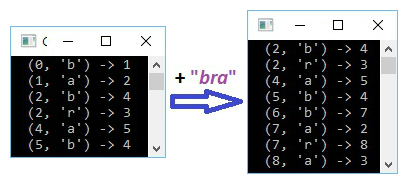
accepts strings bar, ba, baba, bababa and so forth, which are its language. Function δ, as often, is defined by the transition table. Not all cells are full, that means the δ is partially-defined on Q × Σ. In theory it can be easily handled by adding special absorbing state, but in practice it's no need. In programming language we can consider that result of δ in such cases is null, or is None for F#, what have been the choice.
Here is diagram view of the automaton and illustration of its steps during process string ω = baba:

If in some step there is no suitable transition for next symbol of input string ω, or all symbols are passed and current state isn't final, then ω is not accepted (i.e., is rejected) by automaton. For example, the string bra is rejected by the automaton above and not belongs to its language.
Why do we need it
The incremental construction of DFA means adding strings one by one to the language recognized by this automaton. Why do we want doing it? Lets see the automaton below:

It simply recognizes the word son. Now we add to it word win:

We'll discuss later how it can be done. After minimization the resulting automaton contains two different paths for so and wi and one transition for n. In fact, some branches for the common parts were be merged. We could think of it as a some sort of compression. What will happen if now we add to this DFA the word wind? It will increase much more, because there is no word sond, so common branches cannot be stay here anymore:

It's not so interesting. But if we add to previous DFA the word wing instead of wind, and then the word song, automaton will decrease:


That's why we keep automaton minimized. It provides less computational and memory costs in case where DFA recognizes strings that have some common structure rather than set of "independent" or random strings (and that's the purpose of using automata in practice). Now the DFA above accepts the words {son, song, win, wing} and contains only six states and six transitions. Consider that recognized language may be finite (like here) or infinite (like in background section).
Minimization is a quite resource intensive operation. According to straight approach for adding another string we should represent it as a simple automaton, perform union of two automata and then minimize resulting DFA. Instead of this chain of operations, the method proposed by Daciuk and modified by Carrasco and Forcada is to construct a minimal automaton in a single phase by adding new strings one by one and minimizing the resulting automaton on-the fly.2
Implementation
Key points of the algorithm will be illustrated by examples. We'll add string bra to the automaton from the background section. The project itself doesn't contain visualisation, but the samples have been created separately for better clarity.
DFA is defined as a Record, whose values are named according to mathematical definition:
type DFA =
{ Σ : Set<char>;
Q : Set<int>;
q0 : int;
F : Set<int>;
δ : Map<int * char, int>
}
States are an integer numbers, symbols are represented by the char type. Σ, Q and F are defined as a Sets, δ is a Map where key is a Tuple of state and symbol and value is resulting state. It also has method Accept to provide processing input string:
member M.Accept ω =
let rec f ω q =
match ω with
| [] -> (Some q)
| a :: x -> M.δ.TryFind (q, a) |> Option.bind (f x)
f ω M.q0 |> Option.fold (fun _ -> M.F.Contains) false
There are an additional functions to specify some automaton modifications helpful for the algorithm: addState, removeState and addTransition:
let addState q isFinal M =
{ M with
Q = M.Q.Add q;
F = if isFinal then M.F.Add q else M.F }
let removeState q M =
if q <> M.q0
then { M with
Q = M.Q.Remove q;
F = M.F.Remove q;
δ = Set.foldBack (fun a -> Map.remove (q, a)) M.Σ M.δ }
else invalidOp "The initial state cannot be removed"
let addTransition ((q1, a), q2) M =
if M.Q.Contains q1 && M.Q.Contains q2 && M.Σ.Contains a
then { M with δ = Map.add (q1, a) q2 M.δ }
else invalidArg "((q1, a), q2)" "The transition contains wrong elements"
They return copy of the DFA record with modified respective values.
Functions addString and removeString simply call addOrRemove function with true or false as a parameter. We'll see later that adding and removing string differ in just one detail.
The addOrRemove function do follow:
- Creates new state that will be initial (as states are defined by numbers, that it is simply next number following by the maximum state's identifier):
let q0' = M.Q.MaximumElement + 1
- Creates and adds to the automaton new states starting from
q0' (and collects them in a list) using function clone:
let (M', added) = clone flag ω [] q0' (Some M.q0) M
let rec clone flag ω added q' q M =
match ω with
| [] -> Option.foldBack (cloneTrs q') q (addState q' flag M), q'::added
| a :: x ->
match q with
| None -> None,
M |> addState q' false
| Some v -> M.δ.TryFind (v, a),
M |> addState q' (M.F.Contains v) |> cloneTrs q' v
||> clone flag x (q'::added) (q' + 1)

We successively find next state of the automaton step-by-step for each symbol in input string and add new state to the DFA depends on result. If at the another step the current state exists, then its transitions should be cloned to the new state by function cloneTrs:
let cloneTrs q' q M =
{ M with δ = Set.foldBack (fun a ->
Option.foldBack (Map.add (q', a))
(M.δ.TryFind (q, a)))
M.Σ M.δ }
Those new states are called cloned. If result of applying transition function to the current state doesn't exists, then state added at this step will be called queue in the terminology of [Carrasco and Forcada 2002]1.
The flag determines whether we add or remove string. In second case the last added state is not belong to final states, and this is all the difference.
- Adds transitions between new states with symbols from
ω and change initial state for q0':
{ Seq.foldBack2 (fun a (q2, q1) ->
addTransition ((q1, a), q2)) (List.rev ω) (List.pairwise added) M'
with q0 = q0'}

You can see that in code transitions are added in reverse order, but actually it doesn't matter here.
- Then, starting from the "old" initial state and moving by transitions according to
ω, removes those states that became unreacheable using function eliminate:
|> eliminate (Some M.q0) ω M.Q
let rec eliminate q ω R M =
match q with
| Some v when unreachable v M.δ ->
match ω with
| [] -> Set.remove v R, removeState v M
| a :: x -> eliminate (M.δ.TryFind (v, a))
x
(R.Remove v)
(removeState v M)
| _ -> R, M
let unreachable q = not << Map.exists (fun _ -> (=) q)

- Finally, merges equivalent states and return resulting automaton using function
repreg:
||> repreg added
let rec repreg added (R : Set<int>) M =
match added with
| [] -> M
| q :: tail ->
match Seq.tryFind (equiv M q) R with
| Some p -> repreg tail R (merge p q M)
| None -> repreg tail (R.Add q) M
let equiv M p q =
(M.F.Contains p = M.F.Contains q)
&& not <| Set.exists (fun a ->
M.δ.TryFind (q, a) <> M.δ.TryFind (p, a)) M.Σ
let merge p q M =
{ M with
Q = M.Q.Remove q;
F = M.F.Remove q;
δ = Map.map (fun _ -> function
| q_next when q_next = q -> p
| q_next -> q_next)
M.δ }

Using the code and remarks
The attachment for this article is a Visual Studio 2015 solution. The solution consists of one project - console application for .NET Framework 4.5, F# 4.0. The code is presented in Program.fs source file and contains example of defining automaton, adding some string to it and removing other string. The results are printed to console (automata displayed as a lists of states and transitions). All you need to get quick look on the project's work is to open it in Visual Studio and run it by F5 key. The code can also be processed in some interpretator, such as http://www.tryfsharp.org/Create, by extraction the launching snippet from main function into REPL queries.
This realization is one of many possible (basically due to the fact what F# allows to do one thing in different ways). I've tried to write code clear enough to understand the concept, not caring about algorithm complexity and optimization. Moreover, in some cases of F# development best performance demands the combining of functional and imperative approach. You should take it into account if you want to use this method in practice.
Although the code takes less than 200 lines, it probably can be improved (and may contain bugs). Feel free to comment your remarks and to make commits on project's GitHub page IncDFA_algorithm.
Automata pictures are created with FSM simulator.
History
2016-08-03: publication.
References
- Rafael C. Carrasco, Mikel L. Forcada. 2002. Incremental Construction and Maintenance of Minimal Finite-State Automata. Computational Linguistics.
- Daciuk Jan, Stoyan Mihov, Bruce W. Watson, Richard E. Watson. 2000. Incremental Construction of Minimal Acyclic Finite-State Automata. Computational Linguistics.
- Kris Smith. 2009. F# for Architects: Hitting the sweet spot.
- John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman. 2001. Introduction to Automata Theory, Languages, and Computation (2 ed.). Addison Wesley.
