B-Tree: Another Implementation By Java

• Download source - 561.8 KB

Introduction

B-Tree should be familiar to most of college students who take Computer Science as their study major like myself.  Its original purpose is to reduce the time being spent in computer hard drive by minimizing storage I/O operations as much as possible.  The technique has served very well in computer fields such as database and file system.  With the time being, big-data and NoSQL distributed database systems (due to cheap hardware and internet growth) B-Tree and its variants are playing more important role than ever for data storage.

In this article, I won’t discuss about the performance and time measure of B-Tree operations.  These details can be found in [1] and [2].  Instead I'll spend most of the time in this article to discuss and explain how B-Tree data structure and implementation can be done by using Java with my best effort.

Requirements

• JDK 6+ is required to build the core B-Tree and all of its test cases
• JDK 8 is required if you would like to build B-Tree rendering tool that uses JGraphX

What is B-Tree?

B-Tree is a self-balanced tree (i.e. all the leaf nodes have the same height level) data structure.  However unlike other trees such as binary tree, red-black and AVL tree whose nodes have only 2 children:  left child node and right child node, B-Tree’s nodes have more than 2 child nodes.  So sometimes it is called M-way branching tree due to M number of children (M >= 2) that a node in B-Tree can have.

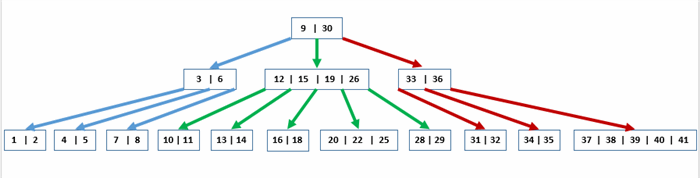Figure 1:  An example of a B-Tree

Root node, internal node and leaf node

Internal nodes are nodes that have children.  Internal nodes lie above the bottom of the tree.  In the figure 1, node [3 | 6], node [12 | 15 | 19| 26] and node [33 | 36] are internal nodes.

Leaf nodes are nodes that don’t have children.  They are the nodes at the bottom of the tree.  In the figure 1, node [1 | 2], node [4 | 5], node [20 | 22 | 25] and node [31 | 32] are some of leaf nodes.

The root node of B-Tree is a special node.  There is only one root node for B-Tree and it lies at the top of the tree.  Depending on the number of items in B-Tree, the root node can be either an internal node or a leaf node.  Node [9 | 30] is the root node of the B-Tree in Figure 1.

B-Tree node’s properties

Each node can have a bunch of keys and a bunch of children (child nodes) where number of children can be either 0 or total number of its keys plus 1.  Let consider node[x].  If node[x] is a leaf node then it won’t have any children.  If it is an internal node then its total number of children is n[x] + 1 where n[x] is the total number of its keys.

B-Tree’s constraints

Let t be the minimum degree of the B-Tree where t >= 2

Constraint #1:  Every node other than the root node must have at least (t – 1) keys.  It is the lower bound for the total number of keys in B-Tree’s node.

Constraint #2:  Every node including the root node must have at most (2t – 1) keys.  So we say the node is full if it has (2t – 1) keys.  It is the upper bound for the total number of keys in B-Tree’s node.

Constraint #3:  Every internal node (other than the root node) must have at least t children.  Every internal node (including the root node) must have at most 2t children.

Constraint #4:  The keys in a node must be stored in ascending order.  For example in Figure 1, node [12 | 15 | 19 | 26] has key 12 < key 15 < key 19 < key 26

Constraint #5:  All the keys of child nodes that are on the left side of a key must be smaller than that key.  In Figure 1, child nodes that are on the left side of key 30 are node [12 | 15 | 19 | 26], node [10 | 11], node [13 | 14] , node [16 | 18], node [20 | 22 | 25] and node [28 | 29] have their keys smaller than 30.

Constraint #6:  All the keys of child nodes that are on the right side of a key must be larger than that key.  For example in Figure 1, child nodes that are on the right side of key 9 are node [12 | 15 | 19 | 26], node [10 | 11], node [13 | 14] , node [16 | 18], node [20 | 22 | 25] and node [28 | 29] have their keys larger than 9.

With constraint #4 and constraint#5, generally all nodes on the left side of a key must have keys smaller than it.

With constraint #4 and constraint#6, generally all nodes on the right side of a key must have keys larger than it.

In Figure 1, the B-Tree’s mininum degree is 3.  So its lower bound is 2 and its upper bound is 5.

If you pay close attention to the example of B-Tree in Figure 1, you’ll notice that a key in any node is actually a range separator of all the keys in the nodes at the lower levels on that key’s left side and right side.

Let look at node [9 | 30], the keys of lower nodes on the left side of key 9 (keys in the nodes that are linked by blue arrows) are smaller than 9.  The keys of lower nodes on the right side of key 9 (keys in the nodes that are linked by green arrows) are larger than 9.  The keys of lower nodes on the left side of key 30 (keys in the nodes that are linked by green arrows) are smaller than 30.   The keys of lower nodes on the right side of key 30 (keys in the nodes that are linked by red arrows) are larger than 30.  This pattern of B-Tree makes the key searching is similar to binary-tree’s key searching.

As long as the B-Tree operations don’t violate the above constraints, it is automatically self-balanced.  In other words, the constraints are devised as such to keep its balance property in check.

The minimum degree (t) is inversely proportional to B-Tree height (h).  Increasement for t will decrease h.  However larger t means more time to spend in nodes for searching keys and trarvesing child nodes.

The concepts and pseudo-code for B-Tree operations

In order to understand how basic B-Tree operations like key searching, insertion and deletion are implemented, some key concepts I would like to introduce before we go to the full implementation details.

Right and left sibling

Right and left sibling of a node are the nodes on its right and left side at the same level.

Figure 2:  Node siblings

In Figure 2, the left sibling of node [18 | 22] is node [3 | 12] and its right sibling is node [33 | 36].  Node [3 | 2] doesn’t have left sibling and its right sibling is node [18 | 22].  The left sibling of node [33 | 36] is node [18 | 22] and it doesn’t have right sibling.

Predecessor and successor of a (internal) node key

In the context of this writing, predecessor and successor of a key in a specified node mentioned here are applied for internal nodes only.

Predecessor is a leaf node within the subtree on the left side of the key and it contains key whose value is the largest one within that subtree.

Symmetrically, successor is a leaf node within the subtree on the right side of the key and it contains key whose value is the smallest one within that subtree.

Figure 3:  Key predecessor and successor

In Figure 3, the predecessor of key 17 is node [13 | 14 | 16] since key 16 is the largest key on its left.  The successor of key 17 is node [19 | 20 | 21] since key 19 is the smallest key on its right.

Similarly the predecessor of key 12 is node [4 | 7 | 6 | 10] since key 10 is the largest key on its left and its successor is node [13 | 14 | 16] since key 13 is the smallest key on its right.

Splitting a node

For insertion, if the node in which we are about to insert is full (it is sometimes also called overflow) we need to split out a node so that it doesn’t violate constraint #2

Figure 4-a:  Splitting in B-Tree

Figure 4-a:  Another splitting in B-Tree

Left and right rotation

For deletion, removing a key from a node can violate constraint #1 (it is sometimes also called underflow).  We can move (borrow) one of the keys from its left or right sibling to that node if one of them has number of keys larger than the lower bound.

Figure 5-a:  Left Rotation

Figure 5-b:  Right Rotation

Merge with the left sibling or right sibling

For deletion if left/right rotation is not possible (i.e. the total number of the keys in left or right sibling of the node exactly equals to the lower bound.  They don’t have extra keys to move to the other nodes) then the merge between that node and one of its siblings has to happen.

Figure 6:  Left sibling merge

General concepts for implementing B-Tree operations

Key searching for B-Tree is simple and straightforward.  If you’re familiar with binary-tree search then you can implement it without any problem.  Nevertheless not as same as binary tree, in B-Tree you need to look through array of keys in a node to verify if the searched key is in that node.  If it is not, we need to make decision for which child node being picked to look further.  The more involved logic is used for the key insertion and the most complex one is the key deletion.  At the high level, however, B-Tree’s insertion and deletion are quite easy to capture:  Key insertion is involved in splitting out a node and key deletion is involved in rotation and merging.  It’s just simple like that.  One important thing we need to be aware in order to make key insertion and deletion possible is:  Before these actions performed on a specified key, it must be in a leaf node.  If the key is in an internal node, we need to swap it to an appropriate key in a leaf node.  With that strategy, we don’t have to worry about the node’s children after adding or deleting a key.

Key searching

Key-Search (searched-key)

    Current-Processed-Node = Root-Node

    While (Current-Processed-Node is not NULL)
        Current-Index = 0

        While ((Current-Index < key number of Current-Processed-Node) AND
                (searched-key > Current-Processed-Node.Keys[Current-Index]))
            Current-Index++
        End While


        If ((Current-Index < key number of Current-Processed-Node) AND
             (searched-key == Current-Processed-Node.Keys[Current-Index]))
            searched-key is found
            Return it (We are done)

        End If

        Current-Processed-Node = Left/Right Child of Current-Processed-Node
    End While

    Return NULL

Key insertion

Figure 7:  An example of key insertion

Split-Node(parent-node, splitted-node)

    Create new-node
    Leaf[new-node] = Leaf[splitted-node]  (The new node must have the same leaf info)

    Copy right half of the keys from splitted-node to the new node

    If (Leaf[splitted-node] is FALSE) Then
        Copy right half of the child pointers from spitted-node to the new node
    End If

    Move some of parent children to the right accordingly

    parent-node.children[relevant index] = new-node

    Move some of parent keys to the right accordingly as well

    Parent-node.keys[relevant index] = splitted-node.keys[the right-most index]

Insert-Key-To-Node(current-node, inserted-key)

    If (Leaf[current-node] == TRUE) Then
        Put inserted-key in the node in ascending order
        Return (We are done)
    End If

    Find the child-node where inserted-key belong

    If (total number of keys in child-node == UPPER BOUND) Then
        Split-Node(current-node, child-node)
        Return Insert-Key-To-Node(current-node, inserted-key)
    End If

    Insert-Key-To-Node(child-node, inserted-key)

Insert-Key(inserted-key)

    If (root-node is NULL) Then
        Allocate for root-node
        Leaf[root-node] = TRUE
    End If


    If (total number of keys in root-node == UPPER BOUND) Then
        Create a new-node
        Assign root-node to be the child pointer of the new-node
        Assign new-node to be the root-node
        Split-Node(new-node, new-node.children[0])
    End If

    Insert-Key-To-Node(new-node, inserted-key)

As you can see, Split-Node() and Insert-Key-To-Node() are the helper functions which are eventually invoked by Insert-Key().  Root node’s update is handled by Insert-Key() and the rest is handled by Split-Node() and Insert-Key-To-Node().  It can be observed that the key insertion always occurs at leaf nodes.  During the insertion path if any node is full, we need to perform the split and restart the insertion process at that point.  By doing this we make sure that B-Tree won’t have any overflow issue for key-insertion.

Key deletion

Figure 8:  An example of key deletion

Delete-Key-From-Node(parent-node, current-node, deleted-key)

    If (Leaf[current-node] == TRUE) Then
        Search for deleted-key in current-node

        If (deleted-key not found) Then
            Return (We are done)
        End If

        If (total number of keys in current-node > LOWER BOUND) Then
            Remove the key in current-node
            Return (We are done)
        End If

        Get left-sibling-node and right-sibling-node of current-node

        If (left-sibling-node is found AND total number of keys in left-sibling-node > LOWER BOUND) Then
            Remove deleted-key from current-node
            Perform right rotation
            Return (We are done)
        End If

        If (right-sibling-node is found AND total number of keys in right-sibling-node > LOWER BOUND) Then
            Remove deleted-key from current-node
            Perform left rotation
            Return (We are done)
        End If

        If (left-sibling-node is not NULL) Then
            Merge current-node with left-sibling-node
        Else
            Merge current-node with right-sibling-node
        End If

        Return Rebalance-BTree-Upward(current-node)
    End If

    Find predecessor-node of current-node

    Swap the right-most key of predecessor-node and deleted-key of current-node

    Delete-Key-From-Node(predecessor-parent-node, predecessor-node, deleted-key)

Rebalance-BTree-Upward(current-node)

    Create Stack

    For each step of the path from root-node to current-node Then
        Stack.push(step-node)
    End For

    While (Stack is not empty) Then
        step-node = Stack.pop()
        If (total number of keys in step-node < LOWER BOUND) Then
            Rebalance-BTree-At-Node(step-node)
        Else
            Return (We are done)
        End If
    End While

Rebalance-BTree-At-Node(step-node)

    If (step-node is NULL OR step-node is root-node) Then
        Return (We are done)
    End If

    Get left-sibling-node and right-sibling-node of step-node

    If (left-sibling-node is found AND total number of keys in left-sibling-node > LOWER BOUND) Then
        Remove deleted-key from step-node
        Perform right rotation
        Return (We are done)
    End If

    If (right-sibling-node is found AND total number of keys in right-sibling-node > LOWER BOUND) Then
        Remove deleted-key from step-node
        Perform left rotation
        Return (We are done)
    End If

    If (left-sibling-node is not NULL) Then
        Merge step-node with left-sibling-node
    Else
        Merge step-node with right-sibling-node
    End If

Delete-Key(deleted-key)

    Delete-Key-From-Node(NULL, root-node, deleted-key)

According to [2], there are two popular ways for key deletion in B-Tree:

1. Do the single pass down the tree:  We need to restructure the tree before we enter into a node so that when we actually delete a key from B-Tree its structure won’t violate any constraints.  Its pseudo code for deletion can be found in [3] and [4]
2. Find and delete the key.  However we need to rebalance upward as key deletion can cause B-Tree’s constraints violation.  My key removal implementation is based on this strategy.  The main entry for deleting a key is Delete-Key().  Later on Rebalance-BTree-Upward() is called to restructure the tree if necessary.  Rebalancing B-Tree is fundamentally involved in left/right rotation and left/right sibling merging.

Java implementation for B-Tree

The source code that implements B-Tree is attached in this writing.  I used NetBeans IDE 8 to create the B-Tree project.  However if you use Eclipse or other Java IDE’s, it should be straightforward to import the java files into yours.  The main java files are BTIteratorIF.java, BTKeyValue.java, BTNode.java and BTree.java.  The generic type is used for B-Tree’s key-value pair so any key that is a subclass of Comparable will work.

Besides B-Tree’s standard operations, it is able to iterate orderly all B-Tree entries by implementing its callback interface.  That’s all for now.  Its future version may implement Java collection iterator interface and it may also have a feature to iterate within a specified range only.

The B-Tree nodes don’t contain any information for their parents.  However we need a node’s parent in some scenarios such as finding its left/right sibling.  It can complicate the actual implementation a bit.

Using the code

Using B-Tree is simple and straightforward like the following:

BTree<Long, String> btree = new BTree<>();
btree.insert(35, "value-35")
     .insert(25, "value-25")
     .insert(12, "value-12")
     .insert(40, "value-40")
     .insert(9, "value-9")
     .insert(4, "value-4")
     .insert(100, "value-100")
     .insert(45, "value-45")
     .insert(80, "value-80")
     .insert(81, "value-81");

String value = btree.search(12);
value = btree.delete(100);

The minimum degree of B-Tree can be found in BTNode.java.  It can be modified with any value that greater than 1 (t >= 2) and it should work without any problems.

Test cases for B-Tree

To me testing is always considered as important as the software itself particularly if we deal with complex logics within a component.  It’s never enough to emphasize how critical the tests are.

I created 7 test cases to validate my B-Tree implementation.  All of them are in BTreeTest.java.  My tests utilize Java TreeMap for key comparison and data validation.

• Test case 0:  Manually and randomly set up, search and delete keys.  Validate all of items for the key order, size and values.
• Test case 1:  Add keys from 1 to 19 and delete few of them.  Validate all of items for the key order, size and values.
• Test case 2:  Add keys from 1 to 32 and delete few of them.  Validate all of items for the key order, size and values.
• Test case 3:  Add keys from 1 to 50 and delete some of them.  Validate all of items for the key order, size and values.
• Test case 4:  Add keys from 1 to 80 and delete from 10 to 30.  Validate all of items for the key order, size and values.
• Test case 5:  Add keys from 0 to 40000, search key from -10 to 100 and delete from 40000 to 0.  Validate all of items for the key order, size and values.
• Test case 6:  Add keys from 40000 to 0, search key from -10 to 200 and delete from 1 to 40000.  Validate all of items for the key order, size and values.

If a test fails for some reasons, it will stop right at that failed point, print out relevant information and exit the test program.  That way we can pinpoint exactly where it fails.

The tool that renders B-Tree

I can surely say that I have made a right decision when I spent time to create this tool for displaying B-Tree in block diagram.  First I thought I just wrote a simple program that would print keys in the text format on the console.  Later I changed my mind when I found a graphical diagram library for Java called JGraphX [6] (by the way the library jar file is included in the zip file).  The tool was worth the time I spent and probably more.  It not only saved lot of hand-drawn papers for me but it also helped me to visually figure out the root causes of bugs in a short time.

Figure 9:  B-Tree Rendering Tool

You can try it out and play around with B-Tree by either adding or removing specified keys.  If you ever catch a bug with this tool, just simply save your steps by clicking on Save button and send the saved file to me.  I’ll use it to reproduce the bug and hopefully fix it next time.

I think the tool itself is deserved a separate article.  However, for the time-being I just stacked it in this article.

Observation and some of my notes

• KISS (Keep It Simple, Sister!):  Don’t overengineer when it is not necessary.  So the question when it is necessary and when it is not.
• I always use earlier-return whenever it’s possible.  It really makes the code logics neat and clean.
• JVM garbage collector is one of the great features in Java platform.  But please don’t think it is panacea for preventing memory leak.  Though there are no resource connections to worry in B-Tree implementation, it still can eat up a lot of memory than it has to when many nodes are still lingered around without being actually used if we don’t handle node splitting and deletion with care.  For large number of min degree and millions of keys residing in B-Tree, lot of nodes eventually won’t be released to JVM GC for recycling if we don’t abandon them correctly.
• Linked list can be replaced for the array in the node structure.  This can make the code more compact (don’t have to deal with array index) and memory usage more efficient (memory spaces are created only when needed).  However the search (and maybe overall performance) will be slow down.
• For node implemented by using array, overall performance can be improved if linear search for keys in the key node arrays is replaced with better search technique like binary search, particularly B-Tree with large min-degree.
• For a project to be successful besides knowledges, correct design and complete tests using/creating right tools is important as well.

Related future works (if time allows)

• If you look into the source codes, you will recognize some logical parts in certain methods are quite the same.  Those are the good candidates for code refactoring.
• As I already mentioned above, implementation for Java standard iterator interface is better than the callback iterator interface.
• Simple file system implementation with B-Tree
• How about distributed B-Tree?  Besides with the way keys are put in the ascending order in B-Tree, it can be a good fit for consistent hashing technique.

Final thoughts

I hope that at this point you’ve already captured full details of B-Tree and how to implement it.  If you did not, at least you got its general concepts and ideas.  Once you digest them, details can be coming later on.

I know dealing with data structure like B-Tree can be dry and boring.  But I guess the beauty is in the eye of the beholder.  Personally B-Tree has been an interesting and challenging data structure in term of its concept and implementation starting when I were in college.  Until lately I’ve needed to find a better solution regarding to data searching and data organization for my current project, B-Tree came to my attention.  A successful implementation only comes after we thoroughly understand all of its important terms and concepts.  We must expect that the implementation details can be overwhelming.  Therefore we should prepare ourselves with a decent debugger, creative test cases and some kind of a visual tool that makes our trouble-shooting easier.  But hey if I can do it, I’m sure you can too.  Until next time, happy coding!

References

[1] Introduction to Algorithms, Third Edition
Chapter 19: B-Tree
http://staff.ustc.edu.cn/~csli/graduate/algorithms/book6/chap19.htm

[2] B-Tree wikipedia
https://en.wikipedia.org/wiki/B-tree

[3] B-Trees
http://www.di.ufpb.br/lucidio/Btrees.pdf

[4] Deletion in B-Tree
http://scanftree.com/Data_Structure/deletion-in-b-tree

[5] B-Tree's notes
http://courses.cs.vt.edu/~cs3114/Fall09/wmcquain/Notes/T15.BTrees.pdf

[6] JGraphX 3.6.0.0 release
https://github.com/jgraph/jgraphx

History

First publish on 11/30/2016

Fix some minor typos and wrong labels on 11/30/2016

Add relationship between min-degree and tree height and fix some minor typos on 12/01/2016