I've recently been updating our series on dithering to include ordered dithering. However, in order to fully demonstrate this, I also updated the sample to include basic color quantizing with a fixed palette.
While color reduction and dithering are related, I didn't want to cover both topics in a single blog post, so here we are with a first post on finding the nearest color via Euclidean distance, and I'll follow up in another post on ordered dithering.
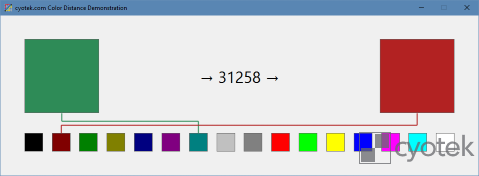
Getting the Distance Between Two Colors
Getting the distance between two colors is a matter of multiplying the difference of each channel between the two colors and then adding it all together, or if you want a formula, Wikipedia obliges handily:

In C# terms, that translates to a helper function similar to the below:
public static int GetDistance(Color current, Color match)
{
int redDifference;
int greenDifference;
int blueDifference;
redDifference = current.R - match.R;
greenDifference = current.G - match.G;
blueDifference = current.B - match.B;
return redDifference * redDifference + greenDifference * greenDifference +
blueDifference * blueDifference;
}
Note that the distance is the same between two colors no matter which way around you call GetDistance with them.
Finding the Nearest Color
With the ability to identify the distance between two colors, it is now a trivial matter to scan a fixed array of colors looking for the closest match. The closest match is merely the color with the lowest distance. A distance of zero means the colors are a direct match.
public static int FindNearestColor(Color[] map, Color current)
{
int shortestDistance;
int index;
index = -1;
shortestDistance = int.MaxValue;
for (int i = 0; i < map.Length; i++)
{
Color match;
int distance;
match = map[i];
distance = GetDistance(current, match);
if (distance < shortestDistance)
{
index = i;
shortestDistance = distance;
}
}
return index;
}
Optimizing Finding the Match
While the initial code is simple, using it practically isn't. In the demonstration program attached to this post, the FindNearestColor is only called once and so you probably won't notice any performance impact. However, if you are performing many searches (for example to reduce the colors in an image), then you may find the code quite slow. In this case, you probably want to look at caching the value of FindNearestColor along with the source color, so that future calls just look in the cache rather than performing a full scan (a normal Dictionary<Color, int> worked fine in my limited testing). Of course, the more colors in the map, the slower it will be as well.
While I haven't tried this yet, using an ordered palette may allow the use of linear searching. When combined with a cached lookup, that ought to be enough for most scenarios.
What About the Alpha Channel?
For my purposes, I don't need to consider the alpha value of a color. However, if you do want to use it, then adjust GetDistance to include the channel, and it will work just fine.
public static int GetDistance(Color current, Color match)
{
int redDifference;
int greenDifference;
int blueDifference;
int alphaDifference;
alphaDifference = current.A - match.A;
redDifference = current.R - match.R;
greenDifference = current.G - match.G;
blueDifference = current.B - match.B;
return alphaDifference * alphaDifference + redDifference * redDifference +
greenDifference * greenDifference + blueDifference * blueDifference;
}
The images below were obtained by setting the value of the box on the left to 0, 0, 220, 0, and the right 255, 0, 220, 0 - same RGB, just different alpha.

History
- 06/01/2017 - First published on cyotek.com
- 07/01/2017 - Updated
- 25/02/2017 - Published on CodeProject
- 26/02/2017 - Corrected bad content
