To solve a matrix equation

Download Matrix_Gauss.zip

Download Matrix_Givens.zip

Download Matrix_LR.zip

Download Matrix_Determinante.zip

Download Matrix_Inv_Cramer.zip

Download Matrix_Householder.zip

Download Polynom_LR.zip

Download Polynom_Givens.zip

Download Polynom_Householder.zip

 

Introduction

If it comes to solve a matrix equation, there is always the elimination algorithm by Carl Friedrich Gauss. But there are many other quite interesting algorithms to solve such a matrix equation. Some are very elegant (at least in my opinion :-), some are quite sophisticated and finally they all do the same and so, the question came to me: Which one is best? That brought me to the idea to compare the different algorithms. In order to do so, I implemented the Algorithm of Gauss, the LU decomposition, elimination by Givens transformation, using the inverse matrix according to Cramer and using Determinants Determinants and then I found the Householder transformation.

O.k. I take that in advance: As long as I didn’t know the Householder transformation, the Givens transformation was my favourite. But now that I know the Householder transformation, I changed my opinion. The Householder transformation is a real great thing and works quick and accurate. But let’s start with the algorithms.

 

Elimination algorithm by Gauss

The classic approach to solve a matrix equation by Gauss is to eliminate all the elements on the left side of the main diagonal in the matrix and to bring (for instance) a 3 * 3 matrix equation like

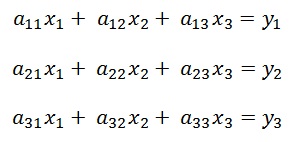
into the form

Now the last equation can be solved for x₃, with x₃ the second equation can be solved for x₂ and with x₂ and x₃ the first equation can be solved for x₁ finally. That’s the basic function of the elimination algorithm by Carl Friedrich Gauss. It consists of 2 parts. First the elimination part and second the solving of the equations for the unknown x values.

The elimination algorithm by Gauss has some disadvantage: If the elements a_ij are bigger than 1, after the elimination the elements in the lower rows become the bigger, the lower it goes. If they are smaller than 1 hey become smaller the lower it goes.

 

A sample matrix equation of

Is brought to the form

With big matrixes that can lead to inaccuracy and in the worst case an overflow. There are the so called pivoting strategies to improve this behaviour and one of this strategies is to pre-process all the rows first in a way that the sum of all the elements of one row becomes close to 1.

 

With this pivoting the same matrix equation looks like this after elimination:

That already looks much better. But still the elimination algorithm by Gauss is not too accurate and it is quite weak in case of ceros in the rows. In such a case, if possible, rows must be switched. If that’s not possible, the algorithm must be stopped and the equation can’t be solved. The pivoting does not help in every case. I tried it on a polynomial interpolation algorithm. There the a_ij values have quite a different distribution and impact of pivoting becomes rather negative. More to this further down.

 

Using a Givens transformation for elimination.

In the Givens transformation a rotation matrix is used to eliminate elements. The idea of the transformation is basically to take two elements a_pq and a_qq and regard them as a 2 dimensional vector. This vector is rotated by the angle φ and the angle φ is minus the angle of the vector in its 2 dimensional room. So the rotation brings the vector into the horizontal direction and eliminates its vertical component which is the element a_pp. The length of the vector is not changed. Therefore the a_ij elements do not grow or shrink as they do it with the Gaussian algorithm. That’s quite an advantage.

In a 5x5 Matrix a rotation matrix looks like:

Where p and q are the 2 dimensions of the plane the rotation takes place. A multiplication of the matrix A with this rotation matrix eliminates element a₂₂. The angle to rotate is calculated as:

To bring the matrix

 

to an upper diagonal matrix the elements a21, a31 and a32 have to be eliminated and therefore 3 different rotation matrixes have to be calculated and A (and the solution vector Y) must be multiplied by them. After that the matrix equation can be solved by the same procedure as used in the algorithm of Gauss.

 

Using this Givens transformation my matrix equation from above looks like this after elimination:

The Givens transformation is much less weak regarding ceros in the rows and it does not have the disadvantage of the growing or shrinking values in the lower rows. That makes it quite stable and accurate. It’s my personal favourite :-)

 

Using a LU decomposition by Prescott Durand Crout

The LU decomposition is a quite sophisticated approach. It’s idea is to decompose the matrix A of the equation Ax = b into a lower triangular matrix and an upper triangular matrix and get LUx = b. The matrixes L and U look like (for a 4*4 matrix):

Now a forward substitution

Ly = b

And a backward substitution

Ux = y

 

Is made and the solution vector x can be calculated in 2 simple loops like:

For i >= j

 

And the formulas for l

 

For i > j

 

The LU decomposition by Crout is a really clever algorithm that shows its performance in special cases like a natural spline interpolation (see www.mosismath.com/NaturalSplines/NaturalSplines.html) where the matrix is a tridiagonal matrix. Beside that it behaves quite similar to the algorithm using the Givens transformation. It performs less multiplications than a Gaussian algorithm and therefore the u_ij elements and u_ij elements do not grow or shrink that much.

Using LU decomposition U and L of my matrix equation look like this after decomposition:

U =

 

L =

The u_ij and l_ij elements do not grow or shrink as much as do the a_ij elements in the Gaussian algorithm. But they do it a bit more than the elements in the Givens transformation. This makes the LU decomposition a bit less accurate than the algorithm using Givens transformations for big matrixes.

 

Using the inverse matrix by Gabriel Cramer

I first got into touch with this approach when I was studying Electrical Engineering and had to solve a matrix equation by my pocket calculator (that’s really long time ago :-). If we invert the matrix A, the matrix equation Ax = b can be written as x = bA^-1. That means multiplying the solution vector by the inverse of A yields the result for the x vector. According to Cramer the inverse matrix can be calculated by building the Determinant of the cofactor matrixes for each element of the matrix A, dividing it by the Determinant of the entire matrix and switching the sign for each element. For a 3 *3 matrix that would look like:

 

Using Determinants by Gabriel Cramer

To solve a matrix equation by the aide of Determinants I got introduced in the Math course while studying and I remember much too good how awful my spaghetti code looked when I implemented it in this time :-) fortunately I could improve my programming skills and implement a bit a better solution now.

Cramer says to calculate the value x_i of a matrix equation Ax = b we have to replace the column I in the matrix A by the b vector, build the determinant of that and divide it by the determinant of the source matrix. For a 3 * 3 matrix equation that would look like:

The part in the denominator is the determinant of A

 

Using Cramers methods to solve a matrix equation might be a very good thing to torture students (at least for us that was the case :-) but for serious applications they do not really suit. Any approach that uses Determinants is rather slow and gets to its limits quite soon. So I did not pursue these algorithms further. But they shall be mentioned as they are really classic (and still interesting to study).

 

Using a Householder transformation

The Householder transformation is another masterpiece of Mathematics I would say. I uses a transformation matrix to eliminates all elements, that have to be eliminated in one row, be just one matrix multiplication. That means to transform a n*n matrix into a right upper matrix it takes just n-1 matrix multiplications. That makes the algorithm really fast and accurate.

The mathematical idea is to regard one row as a vector x and rotate this vector to get all coordinates represented by the elements that should be eliminated to 0 without changing its length x’. Therefore a virtual plane (they call it hyper plane) is placed between the original vector and the resulting rotated vector, this plane is used as mirroring axis and the original vector is mirrored at this axis.

 

 

The reference to this plane (the blue field) is the vector ω. This vector ω is calculated and the transformation matrix U is built as

U = I – 2 * ω * ω^T

 

The vector ω is calculated by subtracting the resulting vector from the original vector and dividing the result by the length of this subtraction as the length of ω is 1.

 

 

That sounds quite simple now. But the way to get there is quite an effort J

See www.mosismath.com/Householder/Householder.html

For a detailed description of the Math.

 

Comparison of the different algorithms

To compare these algorithms I tried several different approaches. With my small 4*4 matrix equation there was no difference at all. So I tried a 10*10 matrix equation. With this on my 64 Bit Inter core 3 computer there were only calculation time issues between the algorithms using Determinants and the others. Regarding accuracy all of them where somewhere in the least significant digits of double values. So I buried the Determinants and went on to a polynomial interpolation. Now the situation became a bit more interesting.

In a polynomial interpolation for n supporting points (x_i, y_i) and looking for the interpolation parameters a_i, we get a matrix equation looking like:

 

 

If the x values are bigger than 1 the element in the top left corner will be the smallest and the element in the bottom right corner the greatest element. If the x values are smaller than 1 it will be vice versa. That’s quite a good benchmark for my algorithms I think J

Now, this constellation is not too good for the Gaussian algorithm. The pivoting cannot help anymore as is does not change the ratio between the biggest and the smallest element in a row. That’s why the Gaussian algorithm gets to its limits here quite soon. I used a little trick and filled the matrix equation upside down. That helps quite a bit. But anyhow, with 12 supporting points it starts to interpolate inaccurate and with 14 points game is over and only the Givens transformation and LU decomposition remain useful. But for a comparison of all 3 I carried out an interpolation with 10 supporting points first. I used a mathematical function that does not bend too much as the polynomial interpolation does not like that. So my test function was y = 10/x² which creates a graph like

 

 

X starts at 1.0 and increases by steps of 0.5.

Regarding accuracy it might be a good idea to compare the values in the matrix after building the upper diagonal matrix for Gauss and Givens and the decomposition in the LU algorithm.

Gauss gets values between 5.004888 and 3.3026311E-103 what makes a ratio of

1.666E103 : 1

That allready shows why the algorithm gets to its limits soon.

 

Givens gets 1345167.95889 to 3.214294 and a ratio of

418496 : 1

 

And the LU decomposition gets 1.0 to 126 in the L matrix and 0.001953 to 8268.75 in the U matrix that makes a max ratio of

4233600 : 1

 

Givens produces the smallest ratio between the biggest and the smallest element in the matrix so far and whit this the best accuracy. O.k it’s not visible with 10 points and not even at 20 points, but if we increase the number of supporting points to 30, the difference becomes visible. Now the graph of the LU decomposition differs quite a bit more from the source shape than the Givens does:

 

The Householder transformation gets 1345167.96 to -3.16 what means a ratio of

425379 : 1

 

That’s slightly bigger than the one of the Givens transformation. That should lead to a bigger inaccuracy, but as the calculation effort in the Householder transformation is the smallest of all the compared algorithms, its accuracy is higher than all the others. It interpolates even 40 supporting points still without a big deviation and it does this in a bit more than 2/3 the time the Givens transformation does it. So it is quite a bit better than the Givens transformation and better all the others :-)

 

Graph created by the LU decomposition with 30 supporting points

Graph created by the Givens transformation with 30 supporting points

 

 

 

Graph created by the Householder transformation with 40 supporting points

The Givens and Householder transformations are maybe not as famous as other algorithms but they are really smart approaches for solving matrix equations. As long as I hadn’t found the Householder transformation, the Givens transformation was my favourite. But now I had to change my opinion :-).

 

For a detailed description of the elimination algorithm by Gauss see
www.mosismath.com/Matrix_Gauss/MatrixGauss.html

For a detailed description of the Givens transformation see
www.mosismath.com/RotationMatrix/RotationMatrix.html

For a detailed description of the LU decomposition see
www.mosismath.com/Matrix_LU/Martix_LU.html

For a detailed description of the method of Cramer see
www.mosismath.com/Determinant/Martix_Determinant.html

For a detailed description of Cramers inverse matrix see
www.mosismath.com/Matrix_inv/Martix_invers.html

For a detailed description of the Householder transformation see
www.mosismath.com/Householder/Householder.html

 

Using the code

My demo projects in c# consist of one single main window. There the algorithms are implemented. I implemented them on Visual Studio 10. I hope you enjoy them :-).