In this article, you will see a program for the Knight's tour on a (square) chess board.

Introduction
This article serves as an answer for CodeProject's weekly code challenge: A knight on a chess board.[^]. The challenge is to write a program for the Knight's tour[^] on a (square) chess board.
My program fully answers the challenge, but it includes a few bonuses:
- It does not only work for 8x8 boards, you can use it for any square chess board (if n >= 5 where n is the count of rows/columns).
- Outputting a plain list of coordinates does not say much to us than just, well, coordinates. That's why my application supports drawing the knight's tour: either as an animated GIF, or as one image with all lines of the tour.
Background
My solution uses Warnsdorff's rule. This is a heuristic for finding the knight's tour that works like this: we move the knight to the square that has the fewest destinations onwards. If that sounds confusing, here is an image to make it clearer:
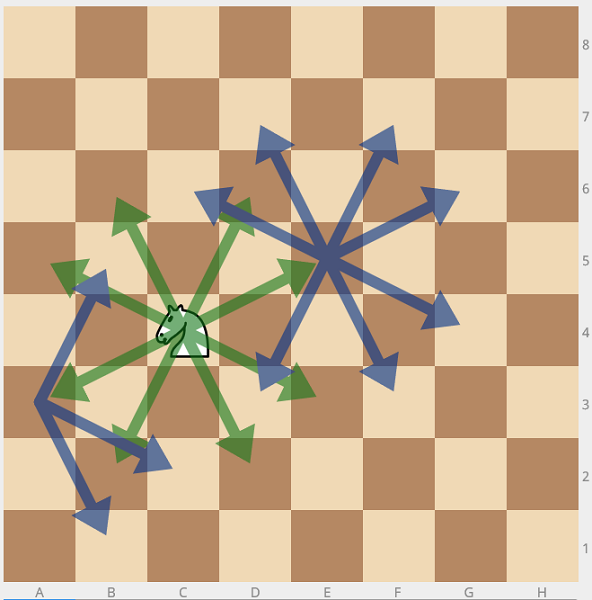
The destinations and (from two squares) the onward destinations for the knight. Board: lichess.org[^]
The green arrows are the knight's possible destinations. The blue arrows (which I only drew from two destination squares, but you should get the idea) show the valid knight moves after moving it like the corresponding green arrow. The c4-a3 move gives 3 onward destinations, c4-e5 gives 7. Warnsdorff's rule says that c4-a3 should be preferred here, because 3 < 7. Also note that for both the destinations ('green arrows') and onward destinations ('blue arrows'), the already-visited squares should be excluded.
On the above image, if we'd draw blue arrows from a5, we would get 3, just like from b3. Which square to pick? Warnsdorff's rule does not specify that. I'm using the following tiebreaker: we pick the square that's the farthest away from the center. "This way, the tour tends to go close to the edges of the board, thereby reducing the apparent risk that the board is split into two or more separate uncovered parts."
Does this tiebreak rule reduce the risk of getting stuck to 0%? No, it might still happen, and then my application will tell you. For non-square boards, the risk of getting stuck appeared to be very high. After several attempts, I could not find a non-square board + a starting position where it did not get stuck. I would guess that Warnsdorff's rule with this tiebreaker do not work that well for non-square boards, but it does work very well for square boards, so that's why my application only accepts square board. However, most of my code will still support a different width and height, because I only observed this after my code was close to finished.
It's also very important to note that on a NxN board where N is odd, your knight must start on a dark square to make the tour possible. (If you're not sure what a 'dark square' would be on an odd board: the corners belong to the dark squares)
Implementation of the Tour Calculation
The Coordinate Class
This class is nothing else than a helper class that has an X and Y property, and some equality methods. Its purpose is to store a coordinate that's used by the other classes. There is not much to say about this class.
public class Coordinate : IEquatable<Coordinate>
{
public int X
{
get;
private set;
}
public int Y
{
get;
private set;
}
public Coordinate(int x, int y)
{
X = x;
Y = y;
}
public override string ToString()
{
return string.Format("({0},{1})", X, Y);
}
public override bool Equals(object obj)
{
if (obj == null || !(obj is Coordinate))
{
return false;
}
return Equals(obj as Coordinate);
}
public bool Equals(Coordinate other)
{
return other != null && this.X == other.X && this.Y == other.Y;
}
public override int GetHashCode()
{
return new { X = X, Y = Y }.GetHashCode();
}
}
The KnightBoard Class
The KnightBoard class is where the tour calculation happens. Let's first go over the fields and properties declared in the class:
BitArray visited;
public int Width { get; private set; }
public int Height { get; private set; }
public Coordinate KnightPosition { get; private set; }
public List<Coordinate> Path { get; private set; }
int[][] directions = new int[][]
{
new int[] { 1, 2 },
new int[] { 2, 1 },
new int[] { -1, -2 },
new int[] { -2, -1 },
new int[] { 2, -1 },
new int[] { -2, 1 },
new int[] { 1, -2 },
new int[] { -1, 2 }
};
visited is a System.Collections.BitArray where the contents indicate which squares have already been visited and which ones haven't.Width and Height are self-explanatory.KnightPosition holds the 'current position' of the knight. In the constructor, this gets set to the starting square. When the actual tour calculation happens, this will be changed often.Path is a list of Coordinates that holds the path for the tour. After the tour calculation method, MakeTour, is called, this will be a complete knight's tour path. If you're wondering why we need visited if we have Path, the answer is simple: we shouldn't use Path to see if a square is visited, because List<T>.Contains is much slower than checking the right bit in the BitArray. This difference is noticeable especially for larger boards.directions holds all possible squares where a knight can go, relative to a given square.
The constructor takes three arguments: width, height (which will be the same because the application will only accept that), and knightPos which indicates the starting position of the knight.
public KnightBoard(int width, int height, Coordinate knightPos)
{
visited = new BitArray(width * height);
Width = width;
Height = height;
visited[ArrayPositionFromCoordinate(knightPos)] = true;
Path = new List<Coordinate>();
Path.Add(knightPos);
KnightPosition = knightPos;
}
The constructor does not do much else than setting values to the fields and properties whose function is explained above.
After the constructor, you see a ArrayPositionFromCoordinate method. Our BitArray visited is a 1-dimension array, but a board is 2-dimension. This method converts a two-dimension coordinate to a one-dimension one, so it can be used by the BitArray.
int ArrayPositionFromCoordinate(Coordinate pos)
{
if (pos.X >= Width || pos.Y >= Height || pos.X < 0 ||
pos.Y < 0) throw new ArgumentException();
return (pos.Y * Height) + pos.X;
}
If you read further in the code, you'll come across the TourExists method. Even though, practically, KnightBoard instances will only see square boards, this method still supports rectangle boards. The rules for existence are taken from the Wikipedia page about the knight's tour[^]:
- If the smaller dimension is at least five, there is a knight's tour. It's possibly open. (Closed means that the knight can move from the last tour square to the first. Open means that it cannot.)
- If it's not at least five, a closed knight's tour is possible unless one (or more) of these conditions is met:
- Both dimensions are odd.
- The smaller dimension is 1, 2 or 4.
- The smaller dimension is 3 and the larger dimension is 4, 6 or 8.
public bool TourExists()
{
int m = Math.Min(Width, Height);
int n = Math.Max(Width, Height);
if (m >= 5) return true;
if (m % 2 == 1 && n % 2 == 1)
return false;
if (m == 1 || m == 2 || m == 4)
return false;
if (m == 3 && (n == 4 || n == 6 || n == 8))
return false;
return true;
}
TourExists is called at the beginning of the application (after taking input) to let the user know if a tour is theoretically impossible.
The next method of KnightBoard is a GetValidDestinations method. It uses the directions array to generate destinations and it only returns those which are in the bounds of the board and which the knight has not visited yet. It's a simple foreach loop over all directions, then checks that it's in the bounds of the array, then checks that it's not visited yet. The method takes an 'origin' parameter and it also does not return a destination when it equals 'origin'.
List<Coordinate> GetValidDestinations(Coordinate origin)
{
List<Coordinate> result = new List<Coordinate>();
foreach (int[] dir in directions)
{
int newX = origin.X + dir[0];
int newY = origin.Y + dir[1];
if (newX < 0 || newY < 0 || newX >= Width || newY >= Height)
{
continue;
}
Coordinate newCo = new Coordinate(newX, newY);
if (visited[ArrayPositionFromCoordinate(newCo)] || newCo.Equals(origin))
{
continue;
}
result.Add(newCo);
}
return result;
}
In 'Background', I mentioned using a tiebreaker: in case of a tie after applying Warnsdorff's rule, I pick the square that's the farthest away from the center. The center is calculated using (Width - 1) / 2.0 and (Height - 1) / 2.0 (minus one, because arrays are zero-based) and then I use the distance formula, \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) but because I'm only comparing distances, I do not have to do the square root. This calculation is performed by the FarthestFromCenter method:
Coordinate FarthestFromCenter(List<Coordinate> options)
{
double centerX = (Width - 1) / 2.0;
double centerY = (Height - 1) / 2.0;
Dictionary<Coordinate, double> coordinatesWithDistanceSquared =
options.ToDictionary(x => x, c => Math.Pow(centerX - c.X, 2) + Math.Pow(centerY - c.Y, 2));
return coordinatesWithDistanceSquared.Aggregate((l, r) => l.Value > r.Value ? l : r).Key;
}
Now we have all helper methods. It's time for the real calculation: the MakeTour method! This method runs a loop while Path.Count is smaller than the amount of squares on the board (note that we don't need to subtract by 1, because our initial position is in Path too).
while (Path.Count < Width * Height)
Inside the loop, the first we do is initialize a Dictionary with destinations and their 'weight', being the amount of moves onwards. As I said in Background, the lower, the better. Then we create a chosen variable to use later. It's set to null initially.
Dictionary<Coordinate, int> weightedCoordinates = new Dictionary<Coordinate, int>();
Coordinate chosen = null;
Time to do actual work. We loop over all valid destinations, and for each one, we get the valid destinations from that square, and the count of that will be the weight.
foreach (Coordinate co in GetValidDestinations(KnightPosition))
{
int optionsFromNewDestination = GetValidDestinations(co).Count;
weightedCoordinates.Add(co, optionsFromNewDestination);
}
If the count of weightedCoordinates is zero, then GetValidDestinations couldn't find anything valid, and that means that the tour is stuck. MakeTour is a bool, so we return false in such a case.
if (weightedCoordinates.Count == 0)
{
return false;
}
Then we only want to keep the coordinates with the lowest weight, to run the tiebreaker on if necessary.
int min = weightedCoordinates.Min(x => x.Value);
List<Coordinate> allMin = weightedCoordinates.Where
(x => x.Value == min).Select(x => x.Key).ToList();
After we got allMin, we have to check if there is only one element in it. If there is, we choose that element. If there are more elements, we run the tiebreaking method.
if (allMin.Count == 1)
{
chosen = allMin[0];
}
else
{
chosen = FarthestFromCenter(allMin);
}
When the chosen square is decided, we add it to the path, update visited and replace KnightPosition.
visited[ArrayPositionFromCoordinate(chosen)] = true;
KnightPosition = chosen;
When the condition for the loop became false, we return true because we successfully found a tour.
}
return true;
The full method looks like this:
public bool MakeTour()
{
while (Path.Count < Width * Height)
{
Dictionary<Coordinate, int> weightedCoordinates = new Dictionary<Coordinate, int>();
Coordinate chosen = null;
foreach (Coordinate co in GetValidDestinations(KnightPosition))
{
int optionsFromNewDestination = GetValidDestinations(co).Count;
weightedCoordinates.Add(co, optionsFromNewDestination);
}
if (weightedCoordinates.Count == 0)
{
return false;
}
int min = weightedCoordinates.Min(x => x.Value);
List<Coordinate> allMin =
weightedCoordinates.Where(x => x.Value == min).Select(x => x.Key).ToList();
if (allMin.Count == 1)
{
chosen = allMin[0];
}
else
{
chosen = FarthestFromCenter(allMin);
}
Path.Add(chosen);
visited[ArrayPositionFromCoordinate(chosen)] = true;
KnightPosition = chosen;
}
return true;
}
BoardDrawing.Draw: Image Representation of the Tour
Our next class is the static class BoardDrawing. It has two methods: Draw, to draw a static image of a path, and CreateGif which uses Draw and Magick.NET to create a GIF for a path. But I'll tell more about that later.
Draw uses .NET's System.Drawing. These are the steps that it takes to create the image:
- The method takes 6 parameters:
List<Coordinate> path: the path to drawint width: the width of the imageint height: the height of the imageint boardWidth: the width (column count) of the boardint boardHeight: the height (row count) of the boardstring file: the file path to save to
- We create an instance of a
Bitmap that we call boardBitmap and we get a Graphics object g from this bitmap. - We use
g.Clear to make the whole Bitmap white rather than black. - We calculate the count of vertical and horizontal lines for the board grid. The border isn't counted because it's drawn separately later. The line counts are just the board width and the board height minus one. Also the distance between the lines is calculated. This is
(width - 2) / boardWidth (or height). Why minus two? Because the border will be 1 pixel large and I don't want to count that for the distance. - The border is drawn using
g.DrawRectangle and the grid is drawn using g.DrawLine in a loop. - We construct an array of
PointFs that will be fed to g.DrawLines. This will be the path of our knight's tour. We use a for-loop and inside this loop, we calculate the x and the y coordinate (on the image) for each coordinate from our tour path. We want this coordinate to be the center of the square, obviously. The x-coordinate is calculated by taking the vertical line distance, multiplying it by the x-coordinate on the chess board and adding up half of the vertical line distance to it. Same for the y-coordinate, but with the horizontal line distance. Then we have the coordinate of the center of the next square in our path. - On the first iteration in the
for loop, we draw a bigger circle in the starting square to indicate that it was the starting square. - Outside the loop, we use
g.DrawLines to draw all lines from the PointF array. - We save the
Bitmap to a file.
This is the code:
public static void Draw
(List<Coordinate> path, int width, int height, int boardWidth, int boardHeight, string file)
{
using (Bitmap boardBitmap = new Bitmap(width, height))
{
using (Graphics g = Graphics.FromImage(boardBitmap))
{
g.Clear(Color.White);
float lineWidth = 1f;
int verticalLineCount = boardWidth - 1;
float verticalLineDistance = (width - 2 * lineWidth) / boardWidth;
int horizontalLineCount = boardHeight - 1;
float horizontalLineDistance = (height - 2 * lineWidth) / boardHeight;
g.DrawRectangle(new Pen(Color.Black, 1), 0, 0,
width - lineWidth, height - lineWidth);
for (int i = 1; i <= verticalLineCount; i++)
{
g.DrawLine(new Pen(Color.Black, lineWidth),
new PointF(i * verticalLineDistance, 0),
new PointF(i * verticalLineDistance, height - lineWidth));
}
for (int i = 1; i <= horizontalLineCount; i++)
{
g.DrawLine(new Pen(Color.Black, lineWidth),
new PointF(0, i * horizontalLineDistance),
new PointF(width - lineWidth, i * horizontalLineDistance));
}
PointF[] linePoints = new PointF[path.Count];
for (int i = 0; i < linePoints.Length; i++)
{
float x = verticalLineDistance * path[i].X + verticalLineDistance / 2;
float y = horizontalLineDistance * path[i].Y + horizontalLineDistance / 2;
linePoints[i] = new PointF(x, y);
if (i == 0)
{
float ellipseWidth = verticalLineDistance / 3;
float ellipseHeight = horizontalLineDistance / 3;
g.FillEllipse(Brushes.Blue, x - (ellipseWidth / 2),
y - (ellipseHeight / 2), ellipseWidth, ellipseHeight);
}
}
if (linePoints.Length >= 2)
{
g.DrawLines(new Pen(Color.Blue, 2), linePoints);
}
}
boardBitmap.Save(file);
}
}
BoardDrawing.CreateGif: Animated GIF for the Path
To create a GIF, we use Magick.NET, the .NET library for ImageMagick. It's available on NuGet[^]. First, we use Draw to create an image for each step, we just have to pass a part of the Coordinate path for that. We store the image in a temporary AppData folder and tell ImageMagick which images to use. Note that this won't work if you have too many images... I tried it with a 50x50 chessboard and after a while, the Bitmap constructor threw an ArgumentException even though my parameters were valid. I guess it was just out of memory. Anyway for smaller chessboards, this works fine. For example a 25x25 chessboard on a 500x500 GIF still worked. I did not do excessive testing on what's the limits because with such chess boards, it's not really fast.
Magick.NET GIF generation works like this: you can create a MagickImageCollection, call .Add to add a file, and then specify an 'animation delay' and repeat that for all images. When that's done, I set the maximum number of colors to 256 to keep the file small (it's not colorful anyway) and I call .Optimize as well.
After the GIF is generated, the directory with the temporary files is deleted.
public static void CreateGif
(List<Coordinate> path, int width, int height, int boardWidth, int boardHeight, string file)
{
string tempDir = Path.Combine(Path.GetTempPath(),
"KnightsTour", "temp-" + Guid.NewGuid().ToString());
Directory.CreateDirectory(tempDir);
using (MagickImageCollection collection = new MagickImageCollection())
{
for (int i = 0; i < path.Count; i++)
{
string filename = Path.Combine(tempDir, i + ".gif");
Draw(path.Take(i + 1).ToList(), width, height, boardWidth, boardHeight, filename);
collection.Add(filename);
collection[i].AnimationDelay =
i != path.Count - 1 ? 50 : 300;
}
QuantizeSettings settings = new QuantizeSettings();
settings.Colors = 256;
collection.Quantize(settings);
collection.Optimize();
collection.Write(file);
}
Directory.Delete(tempDir, true);
}
Program.Main: Taking Input and Running Code
We have all the necessary classes now. It's time to write code to make the application do something while running. It takes the following input:
Width and height of the chess board- The starting square
- Whether you want an output GIF, static image, or no image. If you do want an image, it asks for the
width and the height.
There is no input validation; it's not really an interesting thing to write and it's no part of the challenge anyway.
Here is the code in Main that takes care of the input:
Console.Write("Width and height of chess board: ");
int width, height;
width = height = int.Parse(Console.ReadLine());
Console.Write("Starting square (format: x,y ; zero-based): ");
string[] coordinateParts = Console.ReadLine().Split(new char[] { ',' }, 2);
Coordinate startingSquare = new Coordinate
(int.Parse(coordinateParts[0]), int.Parse(coordinateParts[1]));
Console.Write("Output image? (gif, final, none): ");
string outputImage = Console.ReadLine();
string outputImageFilePath = null;
int imageWidth = -1;
int imageHeight = -1;
if (outputImage == "gif" || outputImage == "final")
{
Console.Write("Output image file path? ");
outputImageFilePath = Console.ReadLine();
if (File.Exists(outputImageFilePath))
{
Console.WriteLine("WARNING! That file already exists,
so this application will overwrite it. Quit if you don't want to do this.");
}
Console.Write("Output image width? ");
imageWidth = int.Parse(Console.ReadLine());
Console.Write("Output image height? ");
imageHeight = int.Parse(Console.ReadLine());
}
Then, a KnightBoard instance is created and it attempts to make the tour. Thereupon, it prints the coordinates.
KnightBoard board = new KnightBoard(width, height, startingSquare);
if (!board.TourExists())
{
Console.WriteLine("There is no tour for this board.");
return;
}
if (!board.MakeTour())
{
Console.WriteLine(string.Join(" ", board.Path.Select(x => x.ToString())));
Console.WriteLine("I'm stuck :(");
return;
}
Console.WriteLine(string.Join(" ", board.Path.Select(x => x.ToString())));
If you want an image, it will generate that as well.
if (outputImage == "gif")
{
Console.WriteLine("Generating GIF...");
try
{
BoardDrawing.CreateGif(board.Path, imageWidth, imageHeight,
width, height, outputImageFilePath);
}
catch (ArgumentException)
{
Console.WriteLine("An ArgumentException occured.
It looks like this happens when the GIF generation takes too much memory. Sorry!");
}
Process.Start(outputImageFilePath);
}
else if (outputImage == "final")
{
Console.WriteLine("Generating image...");
BoardDrawing.Draw(board.Path, imageWidth, imageHeight, width, height, outputImageFilePath);
Process.Start(outputImageFilePath);
}
That was a fun coding challenge :D Thanks for reading!
History
- 11th March, 2017: Initial version
