Introduction
In this article, I will describe the implementation of an efficient Aho-Corasick algorithm for pattern matching. In simple words, this algorithm can be used for searching a text for specified keywords. The following code is useful when you have a set of keywords and you want to find all occurrences of a keywords in the text or check if any of the keywords is present in the text. You should use this algorithm especially if you have a large number of keywords that don't change often, because in this case, it is much more efficient than other algorithms that can be simply implemented using the .NET class library.
Aho-Corasick algorithm
In this section, I'll try to describe the concept of this algorithm. For more information and for a more exact explanation, please take a look at the links at the end of this article. The algorithm consists of two parts. The first part is the building of the tree from keywords you want to search for, and the second part is searching the text for the keywords using the previously built tree (state machine). Searching for a keyword is very efficient, because it only moves through the states in the state machine. If a character is matching, it follows goto function otherwise it follows fail function.
Tree building
In the first phase of the tree building, keywords are added to the tree. In my implementation, I use the class StringSearch.TreeNode, which represents one letter. The root node is used only as a place holder and contains links to other letters. Links created in this first step represents the goto function, which returns the next state when a character is matching.
During the second phase, the fail and output functions are found. The fail function is used when a character is not matching and the output function returns the found keywords for each reached state. For example, in the text "SHIS", the failure function is used to exit from the "SHE" branch to "HIS" branch after the first two characters (because the third character is not matching). During the second phase, the BFS (breadth first search) algorithm is used for traversing through all the nodes. Functions are calculated in this order, because the fail function of the specified node is calculated using the fail function of the parent node.

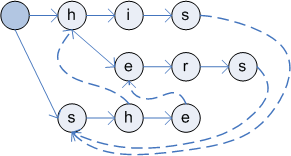
Building of the keyword tree (figure 1 - after the first step, figure 2 - tree with the fail function)
Searching
As I already mentioned, searching only means traversing the previously built keyword tree (state machine). To demonstrate how this algorithm works, let's look at the commented method which returns all the matches of the specified keywords:
public StringSearchResult[] FindAll(string text)
{
ArrayList ret=new ArrayList();
TreeNode ptr=_root;
int index=0;
while(index<text.Length)
{
TreeNode trans=null;
while(trans==null)
{
trans=ptr.GetTransition(text[index]);
if (ptr==_root) break;
if (trans==null) ptr=ptr.Failure;
}
if (trans!=null) ptr=trans;
foreach(string found in ptr.Results)
ret.Add(new StringSearchResult(index-found.Length+1,found));
index++;
}
return (StringSearchResult[])ret.ToArray(typeof(StringSearchResult));
}
Algorithm complexity
Complexity of the first part is not so important, because it is executed only once. Complexity of the second part is O(m+z) where m is the length of the text and z is the number of found keywords (in simple words, it is very fast and it's speed doesn't drop quickly for longer texts or many keywords).
Performance comparison
To show how efficient this algorithm is, I created a test application which compares this algorithm with two other simple methods that can be used for this purpose. The first algorithm uses the String.IndexOf method to search the text for all the keywords, and the second algorithm uses regular expressions - for example, for keywords he, she, and his, it creates a regular expression (he|she|his). The following graphs show the results of tests for two texts of different sizes. The number of used keywords is displayed on the X axis and the time of search is displayed on the Y axis.
The interesting thing is that for less than 70 keywords, it is better to use a simple method using String.IndexOf. Regular expressions are almost always slower than other algorithms. I also tried compiling the test under both .NET 1.1 and .NET 2.0 to see the difference. Although my measuring method may not be very precise, it looks like .NET 2.0 is a bit faster (about 5-10%), and the method with regular expressions gives much better results (about 60% faster).


Two charts comparing the speed of the three described algorithms - Aho-Corasick (green), IndexOf (blue), and Regex (yellow)
How to use the code
I decided to implement this algorithm when I had to ban some words in a community web page (vulgarisms etc.). This is a typical use case because searching should be really fast, but blocked keywords don't change often (and the creation of the keyword tree can be slower).
The search algorithm is implemented in a file StringSearch.cs. I created the interface that represents any search algorithm (so it is easy to replace it with another implementation). This interface is called IStringSearchAlgorithm, and it contains a property Keywords (gets or sets keywords to search for) and methods for searching. The method FindAll returns all the keywords in the passed text, and FindFirst returns the first match. Matches are represented by the StringSearchResult structure that contains the found keyword and its position in the text. The last method is ContainsAny, which returns true when the passed text contains a keyword. The class that implements the Aho-Corasick algorithm is called StringSearch.
Initialization
The following example shows how to load keywords from a database and create a SearchAlgorithm instance:
SqlConnection conn = new SqlConnection(connectionString);
SqlCommand cmd = new SqlCommand("SELECT BlockedWord" +
" FROM BlockedWords",conn);
conn.Open();
ArrayList listWords = new ArrayList();
using(SqlDataReader reader =
cmd.ExecuteReader(CommandBehavior.CloseConnection))
{
while(reader.Read())
listWords.Add(myReader.GetString(0));
}
string[] arrayWords = (string[])listWords.ToArray(typeof(string));
IStringSearchAlgorithm searchAlg = new StringSearch();
searchAlg.Keywords = arrayWords;
You can also use the StringSearch constructor which takes an array of keywords as parameter.
Searching
Searching the passed text for keywords is even easier. The following sample shows how to write all the matches to the console output:
StringSearchResult[] results=searchAlg.FindAll(textToSearch);
foreach(StringSearchResult r in results)
{
Console.WriteLine("Keyword='{0}', Index={1}", r.Keyword, r.Index);
}
Conclusion
This implementation of the Aho-Corasick search algorithm is very efficient if you want to find a large number of keywords in a text of any length, but if you want to search only for a few keywords, it is better to use a simple method like String.IndexOf. The code can be compiled in both .NET 1.1 and .NET 2.0 without any modifications. If you want to learn more about this algorithm, take a look at the link in the next section, it was very useful for me during the implementation of the algorithm and explains the theory behind this algorithm.
Links and references
Future work and history
- 12/03/2005 - First version of this article published at CodeProject.
