Introduction
In my previous publications I’ve already discussed about particular aspects of using several data mining algorithms to accomplish various of tasks which cannot be normally done without performing the actual clustering.
The following article is only a small part of a large analytical research work in the field of computer science and IT, dedicated to the aspects of using clustering and other data mining algorithms to deploy various of software e-commerce tools and components such as recommender engines (RE) allowing to significantly increase the amounts of sales, and, at the same time, simplify the process of finding the products and services of interest by each online customer, having its own personal preferences. In this article, we’ll introduce a principally new clustering algorithm which is a more efficient alternative to the existing k-means and c-means algorithms to perform a better clustering, compared to the already existing algorithms used at the meanwhile.
At this point, we’ll discuss more about the disadvantages of using conventional k-means and fuzzy c-means clustering algorithms, compared to the benefits of using CLOPE clustering algorithm itself.
Particularly, in this article, we’ll formulate a generalized interpretation of the CLOPE clustering algorithm, providing the detailed guidelines on how the following could be easily adopted to accomplish recommendation-specific tasks. As an example of using CLOPE-algorithm, we will demonstrate the code in C# implementing the optimized variation of this algorithm and discuss about the functionality needed to perform the actual clustering.
Background
In this section, we will formulate the new CLOPE clustering algorithm, based on the example of using it to perform the actual clustering of categorized data, having the number of descriptive attributes, such as a dataset of movies stored into the movies and video content online web store’s local database.
Famous K-Means vs. The New CLOPE clustering algorithm
Before we begin the discussion, let’s spend a moment and take a closer look at what particular problems we might reveal while using k-means or c-means clustering to accomplish recommendation-specific tasks.
K-means clustering was actually the first algorithm that was considered to be the most applicable for producing users-to-items recommendations based solely on performing the partitioning of n - observations into k - standalone clusters. According to the following algorithm, each specific cluster normally consists of a pair of two datasets, one - for centroids and another one - for items belonging to a current cluster. Centroids typically represent central items of a cluster, having its features that are very common to each particular item that has been put into a cluster. Specifically, while using k-means clustering to produce users-to-items recommendation, dataset of centroids (i.e. cluster's central items) normally represents a set of users for which a list of recommended items is generated. Also, let's remind that the requirement for performing k-means cluster is that each cluster must contain at least one centroid (i.e. user) and a dataset of multiple items.
In general case, we're initially given a set of observations O = { o1, o2, o3, ... , o(n-1), o(n) }, each one having various of features. In this case, we're asuming that the set of observations contains either users or items data.
To perform k-means clustering, the first what we have to do is to create an initial cluster, in which the first dataset C(k) = { c1, c2, c3, ... , c(q-1), c(q) } contains all users for which we must produce the individual recommendations, and, respectively the second dataset I(k) = { i1, i2, i3, ... , i(s-1), i(s) }, containing all items that are about to be recommended to the set of users Ck. This is typically done by filtering out all items from the entire set of observations.
Since the initial cluster has been created we're starting k-means clustering process by iterating a loop counter variable k -> [0;Nk]. For each index k we're retriving a cluster and for each centroid j -> [0; q] in the current cluster and performing a linear search to find items from the second dataset having similar features with the current centroid j. While performing the linear search, we're actually computing the Euclidian distance between each item in the dataset and the current centroid, selecting only those items having the smallest distance to the current centroid j, and appending them to the dataset for the newly built cluster.
Finally, based on the data previously obtained, we're creating a resulting cluster having only one centroid (i.e. user) and a set of m items having the most similar features (e.g. smallest distance) to the centroid of the target cluster being created. After that, we're proceeding with the next centroid in the list. We’re proceeding with k-means clustering procedure until, we’ve actually ended up with the target list containing a set of clusters having just one centroid that represents a "user" and a dataset of items recommended to them.
Also, there's a number of improvements that allow us to use k-means procedure for performing the total clustering, producing users-to-users and items-to-items recommendations as a part of content-based recommendations paradigm. The very first and obvious improvement, that allows to perform the total clustering, is that while creating an initial cluster we must simply combine users and items data together and fill the first dataset in a cluster with either users or items data from the first half of observations set, and the second dataset with users and items from another half of observations. While performing k-means clustering, for each newly built cluster we're actually shuffling and splitting up an entire dataset of items being found into two subsets. In this case, the first subset is used as a dataset of centroids, and, respectively, the second subset - as the dataset of items for the newly built cluster.
The first problem with k-mean clustring procedure is that it normally uses Euclidian distance as well as, optionally, other distance formulas as a measure of similarity of a particular user and item. While performing the actual clustering we're aiming to find such items having the smallest distance according the the formula mentioned above. In this case, each feature of either user or item is represented as a numerical value of a particular component of a vector residing in multidemensional space. Unfortunately, not all data on features of either user or item can be represented as numeric values or quantitized. To properly define a similarity measure between a current user and item, in many cases, we have to use a slightly different, probability-based, approach to determine the similarity between specific users and items.
Another disadvantage of performing k-means clustering is inablitiy to process a categorized data having the number of multiple descriptive attribute values, and, thus, stored into multidimensional data structures. As many descriptive attributes each user or item would have, as less quality of clustering, and, thus, more misleading recommendation results will be produced.
Finally, k-means clustering algorithm has NP-hard complexity which makes it impossible to use it to cluserize typically huge amounts of recommendation data. That's actually why, the variation of algorithm that performs only users-to-items clustering is actively used at the meanwhile, and the rest of other variants of k-means clustering are rarely used for recommendation purposes.
CLOPE Clustering Algorithm
According to the number of potential problems that persist in the conventional k-means clustering algorithm, it's obviously, that, to perform a better clustering and produce more quality recommendations, we need another clustering algorithm that would use a different approach for measuring the similarity of observations which features cannot be represented as numerical values, providing a desired quality of clustering, and, at the same time, reducing the computational complexity compared to the complex k-means clustering algorithm discussed above.
Before we begin, let's recall that the new CLOPE algorithm, proposed by Yiling Yang, Xudong Guan and Jinyuan You yet in 2002 and adopted by Nikolay Paklin in 2017, is an ideal approach for performing any kinds of recommendations (e.g. users-to-items, users-to-users, items-to-items), since, unlike k-means clustering and other known algorithms, we no longer need to build clusters having sets of centroids and items separately. According to the CLOPE algorithm, we use clusters that have a single dataset combining the data on users and items alltogether, the way it has already been discussed earlier in this article.
To demonstrate the new CLOPE algorithm, we will use a local movies database containing over 200 movies entries. Each specific entry will be placed into a proper cluster based on determining its similarity by the value of more than one descriptive attribute.
Also, unlike k-means clustering, the CLOPE algorithm belongs to the entire class of data mining machine learning algorithms, that exactly conform to “similar tastes in the pasts – similar tastes in the future” paradigm. In the most cases, during the learning phase, we perform the actual clustering model training by using about 50% of all existing users and items entries to the local movies database. According to the CLOPE algorithm, another 50% of data entries will be distributed between pre-defined clusters in the real-time. It means that the CLOPE clustering procedure will determine to which particular cluster each of the data entries, representing a user or item, would belong. However, during the discussion in this article, we will not demostrate the using of CLOPE algorithm in real-time, we will perform the total clustering instead.
Loading Data From File
As we've already discussed, to demonstrate the new CLOPE clustering algorithm we will use a simple flat database of movies merchandised by a video online web store. In this case, we will not use any of existing SQL database engines since the database of movies we will discuss is very simple, containing just one movies entity. Instead, we will store all movies data into a plain text file having the following format:
movies.txt:
0#Gone With the Wind#1939#Clark Gable, Vivien Leigh#Blu-ray#Warner Home Video#Drama-Classics, Drama-Romantic Drama#2/2/2010#58.87
1#Dunkirk#2017#Fionn Whitehead, Tom Glynn-Carney#With DVD, Digital Theater System, 2 Pack#Warner Home Video#War-World War II#12/19/2017#32.79
As you can see from the example above, the values of each field in each record are delimited by '#' character. Each movie record contains the following fields: id, title, year, starring actors, features, studio, genre, release date and price. As we’ve already discussed the values of the most of these attributes are not numerical. That’s why we will use an absolutely different approach for finding similarity between specific movie items, rather than computing the Euclidian distance between their vectors of attributes.
To read the data on each movie from the file in C# we will use System.IO.FileStream to create a simple file object. After that we will use System.IO.StreamReader to instantiate a plain text files reader's object. Since we've already initialized the specific objects, we're iteratively retrieving each line of file performed as a result of System.IO.StreamReader.ReadLine() method invocation. During each iteration we will actually parse each line retrieved from the file by splitting it up into a set of values delimited by '#' character. A set of values obtained from each line of the text file, correspond to specific descriptive attributes (or just a datafields) of a specific movie entry. Then, all values retrieved from each line are stored into the application's internal data memory structures, accessible to the application's routines performing the actual clustering. These internal data structures are thoroughly discussed at the beginning of the "Using the code" section.
Initialization Phase
During the initialization phase, we’re actually preparing a target list of clusters {C}. To do this we're declaring a list of clusters and place N – pre-defined clusters consisting of just one movie item each. The values of attributes of the movie item placed into a pred-defined cluster will represent the attributes common to all movie items within. To do this, we're performing iterations through the dataset of movies, stepping into each movie item Ik and, for each movie item, performing another series of iterations through the target list of clusters. For each cluster Ci we're performing a check if the current movie Ik with particular unique values of attributes has not already been placed into one of the existing clusters in the target list. If not, we place the current movie item Ik into the current cluster Ci. Otherwise if a target list of clusters already contains a specific pre-defined cluster consisting of a movie item having its values of attributes similar to the attributes of the current movie item, then we simply do not create a new pre-defined cluster and are not placing the current movie into it. Instead, we’re proceeding with the next movie item from the movies dataset. Since we’ve obtained a target list of pre-defined clusters, we now can start with the CLOPE clustering process.
CLOPE's Clustering Approach
Before we begin to perform clustering, let's take a short glance at the structure of each clusters built during the clustering phase. Unlike any of the other exisiting algorithms, CLOPE uses an absolutely different clustering approach. It means that, during the clustering phase we will build clusters having a structure we've never used while performing k-means clustering. Specifically, each cluster in the target list will contain only one dataset of items belonging to the entire cluster. Also, each cluster is described by the number of parameters such as cluster's width - W(Ci), height - H(Ci), gradient – G(Ci), S(Ci) – an area of cluster's rectangle, etc.
The width parameter W(C) normally represents the number of groups consisting of movie items having distinct sets of unique attributes values. In turn, another parameter of height H (C) is denoted as the sum of occurrences of each movie item in cluster C, divided by the width of cluster - W(C):
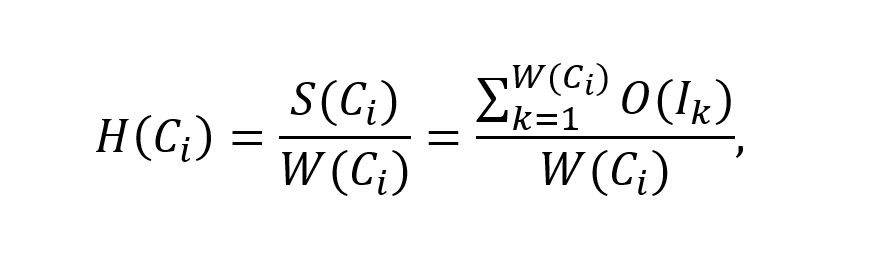
, where H(Ci) - height of the cluster Ci, W(Ci) - width of cluster Ci, S(Ci) - the sum of occurrences of each distinct movie item in cluster Ci (e.g. an area of cluster's Ci retangle), O(Ik) - the number of occurences of movie item Ik in cluster Ci;
Actually, the value of cluster's height H(Ci) is a ratio value of the overall number of movie items in cluster Ci and the number of items having a distinct set of unique attributes values (e.g. the number of various items with absolutely different values of attributes).
In turn, since we've obtained the formula of a cluster's height, now we can easily find the gradient of cluster Ci by using the formula shown below:

, where G(Ci) - gradient of cluster Ci, H(Ci) - height of cluster Ci, W(Ci) - width of cluster Ci, r - value of radical (i.e. power of r) (r >= 2), that serves as a value of repulsion;
Since the values of H(Ci) and W(Ci) cannot be less than 1, we purposely assign this values to 1 for each pre-defined cluster created during the initialization phase. To demonstrate the geometrical meaning of a clusters used in CLOPE-algorithm, let's plot a histogram of a single cluster created:

A histogram of a cluster Ci is actually a graphical representation of its estimated characteristics. All distinct items within a single cluster are plotted along the O-X axis in the decreasing order of their occurences, while the values of occurences of each item Ik appear in the O-Y axis of the histogram. According to the following representation let's find the value of cluster's height H(Ci) estimated as a fraction of the sum of occurrences of each distinct item S(Ci) divided by the width of cluster W(Ci), discussed above. The value of S(Ci) corresponds to the sum of each item's occurences and is equivalent to the area of the cluster's histogram rectangle. As we can see from the Fig.1. shown above, the first column of the histogram contains three entries of item i4, which is O(i4) = 3. Aparently, the second column consists of two entries of item i5: O(i5) = 2. The rest of items i1,i3,i6 occur just once in the cluster, that's why their occurrences will be as follows: O(i1,i3,i6) = 1. By having these values we now can easily compute the sum of occurrences of each distinct item in cluster S(Ci) = 1 + 1 + 1 + 3 + 2 = 8. The value of S(Ci) also normally represents a cluster's rectangle shown on the histogram S(Ci) = 8. Since the value of S(Ci) = 8 and the value of width of cluster W(Ci) = 5 is obtained now we can easily compute the height of cluster H(Ci) = 8 / 5 = 1.6.
According to the CLOPE algorithm, the value of H(C) is used as a measure of the quality of a clustering process itself. As greater value of H(C) as more similarity between an item Ik retrieved from the movies database and items within a current cluster Ci we have. However, it's not enough to estimate the quality of clustering tha t solely relies on the value of cluster's height H(C). It would be more efficient if we would use the value of cluster's gradient that can be calculated as shown above. We will further use the value of gradient to compute the value of delta, which is the main characterstic of cluster Ci that represents a tendency of the cluster to include a movie item Ik.
To illustrate the quality of clustering performed by using CLOPE algorithm and compare it with the similar result obtained by performing k-mean clustering, let's take a closer look at these two results of clustering:

As you can see from the histograms above, the first histogram shown on fig.2a illustrates the results of performing the conventional k-means clustering presented in terms of CLOPE, so it would be easier to compare it to the results of clustering produced by the algorithm being discussed.
Specifically, at this point, let's survey the results of clustering from the second and third cluster histogram based on the values of H(C) and W(C) of specific clusters shown on Fig.2a,b. Obviously, that, clusters { (i4,i5) (i4,i5,i6) } and { (i1,i2) (i1,i2,i3) } have the same value of H(C) and W(C), and, thus, the quality of clustering for these both clusters is absolutely identical. A different case is either the first - { (i1, i2) (i1, i2, i3) (i1,i3,i4) } and the fourth cluster - { (i1,i3,i4) (i4,i5) (i4,i5,i6) }. The histogram of the first cluster contains four unique items having an area of rectangle equal to S(C) = 8 items, and, thus, H(C) = 2.0, H(C)/W(C)= 4. In turn, the fourth cluster contains of W(C) = 5 distinct items and has the same area of rectange equal to H(C) = 1.6, H(C)/W(C) = 0.32. Obviously, that, in this case, the clusters produced as a result of performing CLOPE-based clustering has a tendency to contain more items having the same area of H(C)=1.6, W(C) = 0.32, which most likely would benefit to a better quality of clustering:

, where Profit(Ci) - the value of global profit object function, G(Ck) - a gradient of cluster Ck estimated as G(Ck)=H(C) / W(C)^r, Ci - the overall number of items in cluster Ci, r - regularization coefficient of repulsion.
By using the r as the function's parameter, we regulate the level of similarity of transactions within a single cluster, and, thus, the final number of clusters. This coefficient is normally taken at the initialization phase of the CLOPE-algorithm. As larger value of parameter r ad the lower the similarity level we have and, as the result, the greater number of clusters will be generated.
According to the very basic formulation of the CLOPE-algorithm, during the clustering procedure we're aiming to find such variant of clustering for which Profit(Ci) -> max. This way, we basically perform the profit function maximization tasks.
However, let's recall, beforehand, that, as for performing the actual CLOPE-based clustering, we will not particularly use the global profit objective function. Instead, to determine the similarity of specific clusters and items we will compute the value of delta, which is the algebraic difference between gradient values of an old and newly built cluster.
Clustering Phase
The basic representation of CLOPE clustering algorithm is typically very simple, has the following steps and can be easily formulated as follows:
- Initialize the target list of clusters {C};
- Retrieve the next item Ik, k->[0;m] from the movies dataset and if this is not the end of dataset go to step 3;
- For the current item Ik, retrieve the next cluster Ci, i ->[0;n] from target list if this is not the end of clusters list and proceed with step 4;
- Place the movie item Ik into the current cluster Ci;
- Compute the value of Profit(Ci);
- Perform a check if the the value of Profit(Ci) is the maximum value (e.g. greater than the maximum profit value so far). If not, remove the item Ik from the current cluster Ci in the target list and return to step 3. Otherwise, get back to step 2 to process the next item;
- Proceed with steps 3-6, until we've obtained a distribution for which the value of Profit(Ci) is the maximum;
- Repeat steps 2-7 until all movie items will be distributed to all clusters in the target list;
Actually, there's an oportunity not to combine the specific clusters and items to obtain the high-quality results of clustering. The new CLOPE clustering algorithm has one very important optimization that allows to linearize the total computational complexity of the algorithm. Due to this optimization we basically no longer need to combine each movie item Ik with a specific cluster Ci and then compute the value of global profit to determine the fitness of clustering process itself.
Instead we will use the following algorithm modification based on determining of the fitness for each specific cluster in the target list and a specific item associated with it.
According to the following algorithm-level optimization, the entire process of clustering can be modified and re-formulated as follows:
- Initialize the target list of clusters {C};
- Retrieve the next item Ik, k->[0;m] from the movies dataset and if this is not the end of dataset go to step 3;
- For the current item Ik, retrieve the next cluster Ci, i ->[0;n] from target list if this is not the end of clusters list and proceed with step 4;
- Compute the value of delta for a tuple of the current cluster Ci and item Ik, we're about to place into the cluster Ci;
-
Perform a check if the value of delta is the maximum possible value across the entire list of clusters. If so, place the current item Ik into the cluster Ci and return to step 2. Otherwise, go to step 3;
Delta Function
To compute the value of delta function we need to perform the following steps:
- Assign the current width W(Ci) of the cluster Ci to the new width W(Ci)_New = W(Ci);
- Assign the cluster S(Ci) current size incremented by 1 to the new cluster's S(Ci)_New = S(Ci) + 1;
- Perform a check if the current movie item Ik has not already been placed yet into the current cluster Ci;
- If so, increment the value of the new width W(Ci)_New = W(Ci)_New + 1;
- Compute and return the value of delta as S(Ci)_New * 2 / W(Ci)_New^r - S(Ci) / W(Ci)^r;
In the original CLOPE algorithm whitepaper, the computation of delta is performed for an entire transaction consisting of the number of more than one item. Since, we're about to place at most one movie item to a particular cluster in time, we've purposely modified the delta function value computation rule. These two formulas listed below illustrate the difference between using the original and modified delta computation formula:

, where Sn(Ci) - the sum of each distinct movie item occurrences (e.g. an area of cluster's rectange), Wn(Ci) the new width of cluster Ci after the item Ik has been placed into, S(Ci) - the original area of cluster Ci, W(Ci) - original width of cluster Ci, Nt - the number of transactions.
As you can see from the first formula (from left) the value of delta is basically computed as the difference between the gradient of cluster Ci and a gradient of the same cluster right after a movie item Ik has been placed into it. The width of cluster Ci with movie item Ik included actually differs from the original width of the cluster Ci by 1.
While performing the CLOPE-based clustering we're actually aiming to place the only one movie item in time to the current cluster Ci. That's why, we initially take the value of Nt equal to 1, and substitute it to the same original formula (from left). Obviously, what we'll get is the modified formula (from right) that will further be used to compute the value of delta in case if only one item is added.
Evaluating CLOPE algorithm
Obviously, that, the delta-optimization of the CLOPE algorithm provides the highest liniarization of the computational complexity, which is now p = n x m, proportional to N^2, instead of p =n x m x q proportional to N^3. By using the delta-optimization we actually could linearize the complexity to at least N times, compared to the very first formulation of the CLOPE algorithm. However, by analysing the either original and optimized CLOPE algorithm I've encountered at least two serious issues with the clustering procedure itself.
Computing Similarity
As we've already discussed, to compute the value of delta for a pair of either a cluster and movie item, we need to determine the similarity between a movie item we're about to place and the cluster itself. Just for simplicity of the basic CLOPE algorithm demonstration, we will perform clustering based on determining the similarity of such movie's attributes as movie's genre, starring actors and studio. Specifically, we'll compare the values of these attributes such as if the values of attributes exactly or partially match, it means that two movie items are absolutely similar).
However, since we're about to compare movie items by more than one attribute (e.g. three attributes, at max.) we will use the following approach to compute the overall value of similarity between movie items Ik and It, in case when both attributes exactly match:
- Define the maximum possible similarity measure of each attribute as 1 / Number_Of_Attributes;
- Perform a check if first attribute value in movie item Ik is equal to the value of the same attribute of movie item It. If so add the value of 1 / Number_Of_Attributes to the similarity variable, otherwise go to step 5;
- Perform a check if second attribute value in movie item Ik is equal to the value of the same attribute of movie item It. If so add the value of 1 / Number_Of_Attributes to the similarity variable, otherwise go to step 5;
- Perform a check if third attribute value in movie item Ik is equal to the value of the same attribute of movie item It. If so add the value of 1 / Number_Of_Attributes to the similarity variable, otherwise go to step 5;
- Perform a check if the value of similarity obtained is greater than or equal to the 1 / Number_Of_Attributes * Number_Of_Required. If so, the two movie items Ik and It are considered to be similar, and not, unless otherwise.
To compare particular attributes by a partial match we normally perform the normalization of these attributes values and, finally, parse them comparing their specific fragments. While performing the normalization, we’re actually removing specific attribute’s fragments since these fragments are common to 90% of movie items. To compare the values of attributes of a pair of movie items we’re parsing them to obtain two arrays of tags that are delimited by a set of characters in the original string-based values of these attributes. If these two strings contain the same tags, we assume that the two movie items are similar.
Using the code
Movies_DB Abstract Datatypes (ADT)
To be able to process movies data we need to declare an abstract datatype that defines a each movie's entity. Specifically, we will use a simplified version of movies database containing just one movie entity containing the number of descriptive attributes such as movie's { id, title, year, price, starring actors, studio, genre, release date, price } for each movie in the database:
class Movie : IEquatable<Movie>
{
public Movie()
{
this.ID = "0"; this.Title = "\0"; this.Year = "\0"; this.Starring = "\0";
this.Features = "\0"; this.Studio = "\0"; this.Genre = "\0"; this.Release = "\0"; this.Price = "\0";
}
public Movie(string id, string title, string year,
string starring, string features, string studio, string genre, string release, string price)
{
this.ID = id; this.Title = title;
this.Year = year; this.Price = price;
this.Starring = starring; this.Features = features;
this.Studio = studio; this.Genre = genre; this.Release = release;
}
public bool IsNotEmpty()
{
return (this.ID != "\0" && this.Title != "\0" && this.Year != "\0" && this.Starring != "\0" &&
this.Features != "\0" && this.Studio != "\0" && this.Genre != "\0" && this.Release != "\0");
}
bool IEquatable<Movie>.Equals(Movie other)
{
var similarity = 0.00;
if (this.Genre == other.Genre ||
((this.GenreEqualsByPartialMatch(other)) &&
(this.m_PartialMatch == true)))
{
similarity += 0.33;
similarity += (this.Studio == other.Studio) ? 0.33 : 0;
similarity += (this.Starring == other.Starring) ? 0.33 : 0;
}
return (similarity >= m_AttribsRequired * 0.33);
}
public bool EqualIDs(Movie other)
{
return (this.ID == other.ID);
}
public bool StarringEquals(Movie other)
{
return (this.Starring == other.Starring);
}
public bool StudioEquals(Movie other)
{
return (this.Studio == other.Studio);
}
public bool GenreEquals(Movie other)
{
return (this.Genre == other.Genre);
}
public bool GenreEqualsByPartialMatch(Movie other)
{
return (new GenreComparer().Equals(this.Genre, other.Genre) != false);
}
public string ID { get { return m_ID; } set { m_ID = value; } }
public string Title { get { return m_Title; } set { m_Title = value; } }
public string Year { get { return m_Year; } set { m_Year = value; } }
public string Starring { get { return m_Starring; } set { m_Starring = value; } }
public string Features { get { return m_Features; } set { m_Features = value; } }
public string Studio { get { return m_Studio; } set { m_Studio = value; } }
public string Genre { get { return m_Genre; } set { m_Genre = value; } }
public string Release { get { return m_Release; } set { m_Release = value; } }
public string Price { get { return m_Price; } set { m_Price = value; } }
private string m_ID;
private string m_Year;
private string m_Studio;
private string m_Genre;
private string m_Title;
private string m_Starring;
private string m_Features;
private string m_Release;
private string m_Price;
public bool m_PartialMatch;
public Int32 m_AttribsRequired;
}
class MovieItemStats : IEquatable<MovieItemStats>
{
public MovieItemStats(Movie SrcMovie, Int32 occurrences)
{
this.Movie = SrcMovie; this.Occurrences = occurrences;
}
public bool Equals(MovieItemStats other)
{
return this.Movie.Genre == other.Movie.Genre;
}
public Movie Movie { get { return m_Movie; } set { m_Movie = value; } }
public Int32 Occurrences { get { return m_Occurrences; } set { m_Occurrences = value; } }
private Movie m_Movie;
private Int32 m_Occurrences;
}
class Movies : IEnumerable<Movie>, IEquatable<List<Movie>>
{
private List<Movie> m_Movies;
public Movies() { m_Movies = new List<Movie>(); }
public Movies(List<Movie> MoviesTarget)
{
m_Movies = MoviesTarget;
}
public bool Equals(List<Movie> other)
{
return m_Movies.SequenceEqual(other);
}
public Movie this[Int32 Index]
{
get { return m_Movies[Index]; } set { m_Movies[Index] = value; }
}
public void Add(Movie SrcMovie) { m_Movies.Add(SrcMovie); }
public Movies Take(Int32 Count)
{
return new Movies(m_Movies.Take(Count).ToList());
}
public Movies Skip(Int32 Count)
{
return new Movies(m_Movies.Skip(Count).ToList());
}
public bool SequenceEquals(Movies other)
{
return m_Movies.SequenceEqual(other);
}
public IEnumerator<Movie> GetEnumerator()
{
return m_Movies.GetEnumerator();
}
IEnumerator IEnumerable.GetEnumerator()
{
return this.GetEnumerator();
}
}
class Cluster : IEquatable<Cluster>
{
public Movies m_Movies = new Movies();
public Cluster() { this.UpdateCluster(true); }
public Cluster(Movies SrcMovies)
{
this.Movies = SrcMovies; this.UpdateCluster(true);
}
private List<MovieItemStats> GetMoviesStats()
{
List<MovieItemStats> MovieStats = new List<MovieItemStats>();
for (Int32 Index = 0; Index < Movies.Count(); Index++)
{
Int32 SrcMovie_count = Movies.Where(Movie => Movie.GenreEquals(Movies[Index])).Count();
if (!MovieStats.Contains(new MovieItemStats(Movies[Index], SrcMovie_count)))
MovieStats.Add(new MovieItemStats(Movies[Index], SrcMovie_count));
}
return MovieStats;
}
private double GetHeight()
{
List<MovieItemStats> MovieStats = GetMoviesStats();
return MovieStats.Sum(Stats => Stats.Occurrences) / (double)MovieStats.Count();
}
private double GetWidth()
{
return GetMoviesStats().Count();
}
private void UpdateCluster(bool Initialize = false)
{
if (Initialize == true)
{
this.Width = this.Height = 1;
}
else
{
this.Width = GetWidth(); this.Height = GetHeight();
}
}
public void AddMovie(Movie SrcMovie, bool UpdateRequired = false)
{
m_Movies.Add(SrcMovie);
if (UpdateRequired == true)
this.UpdateCluster(false);
}
public bool Equals(Cluster other)
{
return this.Movies.SequenceEquals(other.Movies);
}
public Movies Movies { get { return m_Movies; } set { m_Movies = value; } }
public double Width { get { return m_Width; } set { m_Width = value; } }
public double Height { get { return m_Height; } set { m_Height = value; } }
private double m_Height;
private double m_Width;
}
}
Loading Data From File
As we've already discussed a the dataset of movies we use the local movies database stored in the plain text file format (*.txt). At this point, we'll demonstrate the code implementing the algorithm for retrieving and parsing movies data from the text file:
private static Movies LoadDataFromFile(string filename)
{
Movies Movies = new Movies();
using (System.IO.FileStream fsFile = new System.IO.FileStream(filename,
System.IO.FileMode.Open, System.IO.FileAccess.Read, System.IO.FileShare.Read))
{
using (System.IO.StreamReader fsStream = new System.IO.StreamReader(
fsFile, System.Text.Encoding.UTF8, true, 128))
{
string textBuf = "\0";
while ((textBuf = fsStream.ReadLine()) != null)
{
string[] entry = Regex.Split(textBuf, "#");
if (entry != null && entry.Count() > 0)
{
var param_aliases = typeof(Movie).GetProperties();
int index = 0; Movie mv = new Movie();
foreach (var param in param_aliases)
param.SetValue(mv, entry[index++]);
if (typeof(Movie).GetProperties().Count() > 0)
Movies.Add(mv);
}
}
}
}
return Movies.Count() > 0 ? Movies : null;
}
To retrive each movie item from text file, we're initializing System.IO.FileStream and System.IO.StreamReader objects and using the System.IO.FileStream.ReadLine() method to read each text line from file and parse each line to retrive specific values of attributes. Then we retrieve the list of properties of Movie class object and assign each value from the current line to each specific property of Movie class object.
Initialization
To initialize the target list of clusters with the number of pre-defined clustering we've implemented the following method:
static Movies Init(string filename, bool partial_match, Int32 attribs_required)
{
Movies Movies = new Movies();
if ((Movies = LoadDataFromFile(filename)) != null)
{
if (m_Clusters != null && m_Clusters.Count() == 0)
{
List<Cluster> ClustersInitialSet = new List<Cluster>();
for (Int32 Index = 0; Index < Movies.Count(); Index++)
{
Movie SrcMovie = Movies[Index];
SrcMovie.m_PartialMatch = partial_match;
SrcMovie.m_AttribsRequired = attribs_required;
Cluster TargetCluster = new Cluster(new Movies(
new List<Movie>() { SrcMovie }));
if (!m_Clusters.Contains(TargetCluster))
m_Clusters.Add(TargetCluster);
}
m_Clusters.AddRange(ClustersInitialSet);
}
}
return Movies;
}
Clustering
To perform the actual clustering, here's the series of methods containing the fragments of code implementing the CLOPE clustering procedure. The first method for performing the actual cluster is GetDelta method that perform the delta value computation:
public static double GetDelta(Cluster SrcCluster, Movie SrcMovie)
{
double Width_New = SrcCluster.Width;
Int32 cluSizeNew = SrcCluster.Movies.Count() + 1;
if (!SrcCluster.Movies.Contains(SrcMovie))
Width_New = Width_New + 1;
return cluSizeNew * 2 / Math.Pow(Width_New, 2) -
SrcCluster.Movies.Count() / Math.Pow(SrcCluster.Width, 2);
}
The actual clustering is performed by executing the code implemented as Clusterize method:
static void Clusterize(Movies Movies)
{
for (Int32 Index = 0; Index < Movies.Count(); Index++)
{
bool Exists = false;
List<Movies> MoviesList = m_Clusters.Select(Cluster => Cluster.Movies).ToList();
for (Int32 MoviessIndex = 0; MoviessIndex < MoviesList.Count() && !Exists; MoviessIndex++)
Exists = (MoviesList[MoviessIndex].Where(Movie
=> Movie.Equals(Movies[Index])).Count() > 0) ? true : false;
if (Exists == false)
{
double delta_max = -1; Int32 cluMaxIndex = -1;
for (Int32 Cluster = 0; Cluster < m_Clusters.Count(); Cluster++)
{
double delta = GetDelta(m_Clusters[Cluster], Movies[Index]);
if (delta > delta_max || delta_max == -1)
{
delta_max = delta; cluMaxIndex = Cluster;
}
}
m_Clusters[cluMaxIndex].AddMovie(Movies[Index], true);
}
}
}
Normalizing And Parsing Data
To compute the similarity between specific movie items by partial match and at the same time perform data normalization, the following two methods NormalizeGenre(...) and Equals(...) were implemented as a part of IEqualityComparer<T> class GenreCompare override:
class GenreComparer : IEqualityComparer<string>
{
public GenreComparer() { }
public List<string> NormalizeGenre(string genre_tags)
{
List<string> GenreTags = genre_tags.Split(new char[] { ' ', ',' },
StringSplitOptions.RemoveEmptyEntries).Distinct().
Where(Tag => Tag.Length > 1).ToList();
return GenreTags.Select(Tag => (Tag.IndexOf('-') > -1) ?
Tag.Substring(0, Tag.IndexOf('-')) : Tag).Distinct().ToList();
}
public bool Equals(string genre_tags1, string genre_tags2)
{
Int32 EqualsCount = 0;
List<string> tags_list1 = NormalizeGenre(genre_tags1);
List<string> tags_list2 = NormalizeGenre(genre_tags2);
if (tags_list1.SequenceEqual(tags_list2)) return true;
for (Int32 Index1 = 0; Index1 < tags_list1.Count(); Index1++)
for (Int32 Index2 = 0; Index2 < tags_list2.Count(); Index2++)
if (tags_list1[Index1].Equals(tags_list2[Index2])) EqualsCount++;
return (EqualsCount > 0) ? true : false;
}
public int GetHashCode(string obj)
{
throw new NotImplementedException();
}
}
Also we've implemented the series of functions for performing various of servicing operations such as rendering the clustering results or checking the validity of each cluster:
static bool IsValidCluster(Cluster TargetCluster)
{
bool isUnique = false;
Movie mvTarget = TargetCluster.Movies[0];
isUnique = TargetCluster.Movies.Skip(1).Where(Movie =>
Movie.Equals(mvTarget)).Count() == TargetCluster.Movies.Count() ? true : false;
return !isUnique;
}
static void PrintClusters()
{
Console.WriteLine("Clustering Statistics...");
Console.WriteLine("========================");
for (Int32 Index = 0; Index < m_Clusters.Count(); Index++)
{
bool IsValid = IsValidCluster(m_Clusters[Index]);
Console.WriteLine("Cluster {0}: (Valid: {1}, Movies: {2})", Index,
(IsValid == true) ? "Okey" : "Failed", m_Clusters[Index].Movies.Count());
}
Console.WriteLine("\nClustering Results...");
Console.WriteLine("=======================");
for (Int32 Index = 0; Index < m_Clusters.Count(); Index++)
{
Movies Movies = m_Clusters[Index].Movies;
Console.WriteLine("Cluster {0} (Genre: {1}) (Valid: {2}):",
Index, Movies[0].Genre, (IsValidCluster(m_Clusters[Index])) ? "Okey" : "Failed");
Console.WriteLine("==================================================================");
for (var Movie = 0; Movie < Movies.Count(); Movie++)
{
String movie_row = "\0";
var param_aliases = typeof(Movie).GetProperties();
foreach (var param in param_aliases)
movie_row += param.GetValue(Movies[Movie]).ToString() + " ";
Console.WriteLine("{0}", movie_row);
}
Console.WriteLine();
}
}
The main function for this CLOPE .NET application:
static void Main(string[] args)
{
Console.WriteLine("CLOPE - Clustering Algorithm v.1.00a by Arthur V. Ratz @ CodeProject.Com");
Console.WriteLine("=====================================================================\n");
string filename = "\0";
string MatchOption = "\0"; bool PartialMatch = false;
Console.Write("Input data file name: "); filename = Console.ReadLine();
Console.Write("Input the number of required attributes: ");
Int32 AttribsRequired = Int32.Parse(Console.ReadLine());
Console.Write("Clusterize by partial match: (y/n)");
do
{
MatchOption = Console.ReadLine();
PartialMatch = ((MatchOption == "y") || (MatchOption == "yes")) ?
(((MatchOption != "n") && (MatchOption != "no")) ? true : false) : false;
} while (((MatchOption != "y") && (MatchOption != "yes")) &&
((MatchOption != "n") && (MatchOption != "no")));
Console.WriteLine("\n");
Clusterize(Init(filename, PartialMatch,
AttribsRequired)); PrintClusters(); Console.ReadKey();
Console.ReadKey();
}
Points of Interest
In this article, we've thoroughly discussed about the revolutionary new CLOPE clustering algorithm. However, not all topics that might be interesting to the audience of readers are covered in this article. Probably someone of the programming and algorithms enthusiasts will spend a bit of time to evaluate this algorithm by implementing the algorithm’s learning phase and survey its characterists in real-time, compared to the conventional k-means clustering. Also, it's worth to examine the following algorithm with different datasets and various numbers of attributes values.
History
- April 27, 2018 - The first revision of this article was published;
