Permutations: Fast Implementations and a New Indexing Algorithm allowing Multithreading

• Download source code - 46.7 KB
• Latest version on GitHub

Introduction

This article is the continuation of a StackOverflow question asked by SimpleVar: “Generating permutations of a set (most efficiently)”. It shows many fast implementations of permutation algorithm. There is also a contribution by providing a unique way to index permutation allowing to get a specific permutation based on lexicographical order.

Contents

• Many permutation algorithm implementations
• A new algorithm that enables indexing of lexicographic permutations
• A multithreaded algorithm implementation that is a mix of two algorithms: SaniSinghHuttunen and OuelletIndexed
• Code that includes a benchmark and all presented algorithm implementations
• Some additional general information about permutations and multithreading

Background

Permutation Definition

According to Wikipedia:

In mathematics, the notion of permutations relates to the act of arranging all the members of a set into some sequence or order, or if the set is already ordered, rearranging (reordering) its elements, a process called permuting. These differ from combinations, which are selections of some members of a set where order is disregarded. For example, written as tuples, there are six permutations of the set {1,2,3}, namely: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), and (3,2,1). These are all the possible orderings of this three element set. As another example, an anagram of a word, all of whose letters are different, is a permutation of its letters. In this example, the letters are already ordered in the original word and the anagram is a reordering of the letters. The study of permutations of finite sets is a topic in the field of combinatorics.

Permutation Vs. Combination

Some people could mix permutations and combinations. In permutations, the number of items is always the same whereas it’s not the case for combination.

Example of Permutation and Combination for 3 items (a,b,c):

Permutation Count = n!	Combination Count = 2n
a, b, c	<empty>
a, c, b	a
b, a, c	b
b, c, a	c
c, a, b	a, b
c, b, a	b, c
	c, a
	a, b, c

Additional Information

The number of possible unique permutations of a set of x elements is x! (x factorial). Which is 1 * 2 * 3 * …* x. The number of possibilities grows very quickly.

Some usage is required to get permutations in lexicographic (sorted) order while others only need all permutations in any order.

Permutation Algorithm/Implementation

Many actual algorithm implementations are based on the current result to find the next one.

When testing code, it could be useful to test all the permutations of a set of possibilities. To do so, an algorithm that enumerates all possible permutations of a set of values could be used. Because the number of possible permutations grows in factorial order, it is often looked to choose the fastest algorithm in order to save a maximum amount of time in doing useful work, not just finding permutations.

Single threaded algorithm has the ability to provide permutations in lexicographic order, while multithreaded algorithms would not guarantee the results in any specific order because otherwise it will be slowed down by the ordering mechanism and lose its main concurrent advantage.

Author	Algo name in benchmark	Based on algorithm	Lex1	Threadable2	Comment (safe code/LINQ/Threadable/etc.)
Ouellet	OuelletHeap	Heap	No	No	Fastest ST overall
Sani Huttunen	SaniSinghHuttunen	Knuths	Yes	No	Fastest ST lexico
Erez Robinson	Erez Robinson	? QuickPerm	No	No
SimpleVar	SimpleVarUnsafe	?	No	No	Unsafe code
SimpleVar	SimpleVarLex	?	Yes	No
Sam	Sam	?	Yes	No
Ziezi	Ziezi	?	No	No	EO: I slightly modify the code in order to make it work with the benchmark.
Ouellet	Ouellet Indexed	Ouellet	Yes	Yes	See detail in section Fastest algorithm/implementation details
Lex1 Enumeration of permutation is done lexicographically Threadable2 Any algorithm where the current permutation requires the previous one is discarded as threadable because we can’t start enumeration of permutations from any specific place (with known code).

Table 1: List of C# algorithms with 2 up votes or more on StackOverflow “Generating permutations of a set (most efficiently)” (2018-06-5)

Benchmark Results

Next three benchmarks show results from the provided benchmark. A graphic follows each result table to facilitate the observation of speed differences between algorithm implementation.

The first graph is a global view of every implementation. But the second and third have less and less algorithm implementation in order to show only significant ones which have speed close together.

The ratio is simply the time taken by implementation divided by the time of the fastest implementation. That’s why the ratio is always “1” for the fastest one.

All tests were done on a machine with a hyperthreaded CPU with 6 real threads = 12 threads.

Parallelizing (using all threads) bring a clear advantage of around 5 times faster on the machine used.

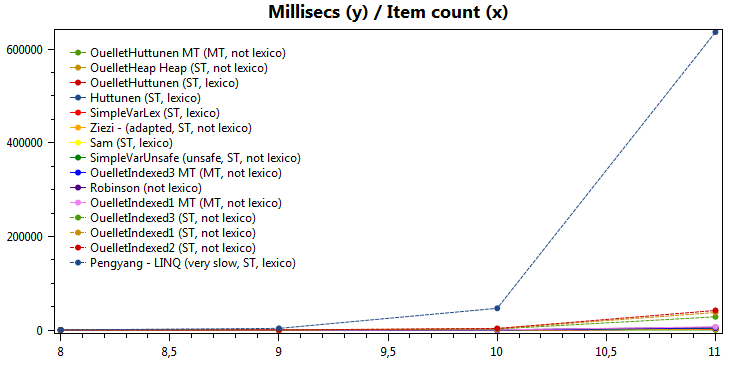
Benchmark result for all algorithms for 11 items (11! = 39 916 800 permutations)

Algo	8!	8! Ratio	9!	9! Ratio	10!	10! Ratio	11!	11! Ratio
OuelletHuttunen MT (MT, not lexico)	1	1	3	1	25	1	292	1
OuelletHeap Heap (ST, not lexico)	2	2	15	5	150	6	1659	5,68
OuelletHuttunen (ST, lexico)	2	2	15	5	158	6,32	1741	5,96
Huttunen (ST, lexico)	2	2	16	5,33	161	6,44	1778	6,08
SimpleVarLex (ST, lexico)	2	2	18	6	179	7,16	1966	6,73
Ziezi -(adapted, ST, not lexico)	2	2	18	6	180	7,2	2004	6,86
Sam (ST, lexico)	4	4	31	10,33	326	13,04	3474	11,89
SimpleVarUnsafe (unsafe, ST, not lexico)	5	5	32	10,66	320	12,8	3696	12,65
OuelletIndexed3 MT (MT, not lexico)	7	7	34	11,33	341	13,64	4606	15,77
Robinson (not lexico)	7	7	49	16,33	525	21	6151	21,06
OuelletIndexed1 MT (MT, not lexico)	32	32	55	18,33	582	23,28	6893	23,60
OuelletIndexed3 (ST, not lexico)	21	21	208	69,33	2338	93,52	28328	97,01
OuelletIndexed1 (ST, not lexico)	31	31	299	99,66	3069	122,76	37518	128,48
OuelletIndexed2 (ST, not lexico)	40	40	332	110,66	3433	137,32	41965	143,71
Pengyang - LINQ (very slow, ST, lexico)	317	317	3626	1208,66	46543	1861,72	636744	2180,63

Benchmark result for efficient algorithms for 13 items (13! = 6 227 020 800 permutations)

Algo	8!	8! Ratio	9!	9! Ratio	10!	10! Ratio	11!	11! Ratio	12!	12! Ratio	13!	13! Ratio
OuelletHuttunen MT (MT, not lexico)	4	4	15	1	33	1	326	1	3967	1	44517	1
OuelletHeap Heap (ST, not lexico)	1	1	15	1	149	4,51	1641	5,03	19727	4,97	257105	5,77
Huttunen (ST, lexico)	1	1	15	1	162	4,90	1873	5,74	21179	5,33	275596	6,19
OuelletHuttunen (ST, lexico)	2	2	15	1	157	4,75	1736	5,32	20806	5,24	275854	6,19
SimpleVarLex (ST, lexico)	2	2	18	1,2	178	5,39	1975	6,05	23594	5,94	310474	6,97
Ziezi(adapted, ST, not lexico)	1	1	17	1,13	180	5,45	1963	6,02	23577	5,94	312943	7,02

Benchmark result for the 4 best algorithms for 16 items (16! = 20 922 789 888 000 permutations)

Algo	11!	11! Ratio	12!	12! Ratio	13!	13! Ratio	14!	14! Ratio	15!	15! Ratio	16!	16! Ratio
OuelletHuttunen MT (MT, not lexico)	81	1	1047	1	13025	1	165949	1	2439328	1	36169342	1
OuelletHeap Heap (ST, not lexico)	334	4,12	4202	4,01	52733	4,048	715050	4,30	10740155	4,40	1,8E+08	4,98
OuelletHuttunen (ST, lexico)	410	5,06	5415	5,17	62251	4,77	851321	5,13	12787225	5,24	2,03E+08	5,61
Huttunen (ST, lexico)	401	4,95	4826	4,60	64608	4,96	869725	5,24	13089221	5,36	2,08E+08	5,73

Fastest Algorithm/Implementation Details

Sani Huttunen

Sanis algorithm implementation is the fastest lexicographic algorithm tested.

Ouellet Heap

This is a simple implementation of the “Heap” algorithm found on Wikipedia. The speed of the algorithm is due to the fact that it is only swapping 2 values per permutation, always, not more. There is no recursion. The number of external calls has been minimized to maximize the speed. The memory footprint is very small.

According to the benchmark, it is the fastest, single threaded, algorithms. But it can’t be easily multithreaded (parallelized) because there is no way to start from any position (index). Also, because the output is not in lexicographic order, it does add another layer of complexity to parallelize it.

Ouellet Indexed

Indexing permutations allow getting a specific permutation. Each permutation has its own unique index. The algorithm is able to generate the permutation only based on its lexicographic index. It does not depend on any previous permutation or any other states. I created that algorithm in order to be able to parallelize permutation algorithm. Being able to get a permutation from an index has:

Advantages

• Indexing permutations enables easy parallelization of this algorithm. It also enables parallelization of any other permutation algorithm that has two characteristics: 1- generation of permutation is done in lexicographic order, 2- next permutations depends on the current one.
• It enables to get directly any set of permutations in order to use that specific set without having to find all the previous ones. It could be very useful to replay specific set of permutation values. It would have been super useful when I was developing/testing my Ouellet Convex Hull Algorithm.

Disadvantages

• The algorithm is extremely slow. Although after parallelizing this algorithm, it still stays in the snail department for performance. To be useful for parallelization, it should be –used with another fast algorithm where usage of OuelletIndexed is only used to find the first permutation of a long sequence.
  Note: Because the actual implementation index parameter is based on the type “long”. The maximum number of items supported is 20. That is due to:
  • 20! < 2^63 (63 bits for signed long)
  • 21! > 2^64 (64 bits for unsigned long)

A helper function has also been added to the algorithm class to get the index of any given permutation which can be called wherever needed.

Many modifications were introduced during the course of the development of this algorithm. Most of them were to improve speed. Three versions actually exist which are primarily the same algorithm between version 1, 2 and 3.

Version of OuelletIndexed	Description
1	First working iteration of finding a permutation from left to right.
2	Attempt to improve performance of version 1 by removing the calculation of factorial.
3	Replaced the leftValues list from a “List” of values to an array of Boolean value indicating if the value is used or not. Instead of having to remove values into a “List”, values to be removed are simply marked as being used into a corresponding boolean array.
4	Attempt to find a permutation from right to left. It never worked.

Although version 3 is a lot faster than version 1, it is still extremely slow, either used in its multithreaded version.

How the Algorithm Works

permutationIndex	Permutation (colIndex: 3 = left most, 0 = right most)
0	abcd
1	abdc
2	acbd
3	acdb
4	adbc
5	adcb
6	bacd
7	badc
8	bcad
9	bcda
10	bdac
11	bdca
12	cabd
…	…

Table 2: List of first permutations for 4 values (4! = 24)

Note the repetition in the list of values in Table 2. If we consider column 0 as the right most and column 3 as the left most, the first 6 entries will have “a” in it. We can observe:

• Column 3 has entries that repeat 6 times.
• Column 2 has entries that repeat 2 times.
• If we had a column 4, we would have 24 entries that would repeat 24 times.

Column index entries repetition is factorial dependent. The algorithm uses a special data structure to manage available values. At the start, each value is placed into a list where the leftmost would be at index: 0 and the right most at index: (number of values -1). That list is called leftValues list. It is the list of potential values that is left to be inserted as part of the currently calculated permutation.

For our example, at the beginning of the algorithm, values are placed in the LeftValues list in this order:

• valueIndex = 0 : a
• valueIndex = 1 : b
• valueIndex = 2 : c
• valueIndex = 3: d

Looking at repetition in the table, we can see that the number of repeating entries per column is linked to the function of factorial of the column index. If we use colIndex as column index and valueIndex as value index, we can express the value index as being function of both: permutation index and the column index. The formula is:

valueIndex = permutationIndex / colIndex! **

The preceding formula works for the left most column. But it can’t be applied for all other columns, mainly due to the following problems:

1. Using the formula would result in values that are already used previously. Like for permutations index 0. The formula would give: aaaa.
2. For any column that is to the right of the left most one, we will soon get value index that is greater than the possible valueIndex. For example, for the preceding input of 4 values: when permutationIndex = 8 and the permutation is “bcad”, calculating the valueIndex of the columnIndex=2 is 8/2! = 4. But a valueIndex of 4 is bigger than the maximum value index which should be between 0 and 3 inclusively.

Problem 1 could be easily solved using the leftValue list of all potential values and remove each selected value when we assign one to a column index. Removing a value in the list of leftValues would change correspondence between the index and its value and all the following values in the list after that index. But it is exactly what it should be. The new value for that value index will represent what should be used at that index. It is also true for all following values, if any.

Problem 2 could easily be fixed by applying another calculation to permutationIndex in order to convert it into a range where the preceding formula ** will become valid. To do so, we just need to get the modulo of permutationIndex by the factorial of (colIndex +1).

The final formula to get valueIndex relative to permutation index and column index is:

valueIndex  = PermutationIndex % (columnIndex+1)! / columnIndex!

That gives the relative index in the list of leftValues (not yet used values). Each time we pick a value, it is removed from the leftValues list. We should process column from left to right. It should only leave one value in the list when processing the last column and that value should be the right one for that column.

This algorithm is very slow. It could be used to find all permutations if desired. To get all permutations, we can iterate over all possible permutation index which is: 0 < permutationIndex < (n!-1) for n values. But doing so will take a lot more time than using a more efficient algorithm. Although very slow, it has a great advantage over most algorithms: It could retrieve a specific indexed permutation. That advantage is the key necessary to parallelize other lexicographic permutation algorithm. Many algorithms depend on the actual value to find the next one. To parallelize those algorithms, we need to start permutation sequence at specific index. In order to enable that, usage of a permutation indexer is required. That is why this algorithm is so useful.

OuelletHuttunen

OuelletHuttunen is an algorithm that could find a sequence of any number of permutations starting from any index. The sum of the first index plus the number of permutation chosen should stay less than the number of total permutations possible.

Using only OuelletIndexed would do the job but very slowly. That is because OuelletIndexed is extremely slow. To improve performance, we only use OuelletIndexed where there is no other solution. OuelletIndexed is only used to find the first permutation of a sequence and then we use another algorithm to iterate over that sequence of permutations.

The algorithm implementation that has been retained is to use OuelletIndexed in conjunction with Sani Huttunens implementation because it is the fastest one to be in lexicographical order.

The final algorithm called OuelletHuttunen is composed of two different algorithms in order to achieve best performance:

1. Ouellet Indexed for the first permutation
2. SaniSinghHuttunen for all other permutations of the sequence

Note: SaniSinghHuttunen algorithm has been chosen over OuelletHeap although OuelletHeap is faster. That is because the index of OuelletIndexed is based on lexicographical order and the OuelletHeap algorithm does not provide permutations lexicographically. Both algorithms should be in sync together, and thus should use the same permutation order. SaniSinghHuttunen performance is very close to OuelletHeap and its results are in lexicographical order.

The final algorithm could easily be parallelized, like it is done in the benchmark.

There is one thing that could be observed for count of items around 8 or less. Because around “8!”, the number of permutations is so low, the time required to start/initialize threads will weigh more than finding the permutations themselves.

Important Threading Note

In the benchmark, during tests of algorithms, there was a global variable used to calculate the number of iterations. The count was used to ensure the number of permutations were correct: permutationCount = valueCount!.

Using a simple global variable to count the number of permutations was not a valid choice with multithreaded implementation. The variable increment did not happen on each permutation because of thread concurrency. Adding a locking mechanism, using either SpinLock or Interlocked class, fixed the problem. But it adds a great amount of latency. Removing locking mechanism and letting the global variable alone accelerate a lot the speed (with counting errors) but the performance was very far from what was expected. It took a little while before realizing the source of the problem was due to the same variable accessed from different thread where each thread was modifying that value. That causes the known problem of “False Sharing”. That is due to the processor architecture and its thread cache. It is very similar to the problem I fixed with Interlocked (or SpinLock) class but instead of being at the code level, it happens at the CPU level. To have a more realistic time taken by each algorithm, I set a test that does absolutely nothing. This way, the time recorded by an algorithm is purely the time to find permutations, nothing else.

I think that a good rule of thumb to remember in order to get the best performance when parallelizing algorithm, it is to avoid any shared read/write variables between threads whenever possible. A read only variable should not create the same latency effect.

Benchmark Code

All the code is provided in GitHub under https://github.com/EricOuellet2/Permutations

The code is done in C# with the GUI in WPF.

The algorithms used in the benchmark are in C# and comes from answers to the Stack Overflow question: Generating permutations of a set (most efficiently). Some minor adjustment could have been done in order to fit into the benchmark.

Conclusion

Thanks to SimpleVar for asking the question Generating permutations of a set (most efficiently) on StackOverflow. It was challenging and fun to try to find the best answer. I learned a few nice things.

I hope you liked this article and you also learnt something or took advantage of the code.

History

• 3^rd July, 2018: Initial post
• 14^th July, 2018: Minor corrections and additions, added history
• 20^th July, 2018: Minor corrections (syntax correction, positioning of bullets)