Introduction
In machine learning, support vector machines (SVMs) are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis (Wikipedia). This article is a summary of my learning and the main sources can be found in the References section.
Support Vector Machines and the Sequential Minimal Optimization (SMO) can be found in [1],[2] and [3]. Details about a simplified version of the SMO and its pseudo-code can be found in [4]. You can also find Python code of the SMO algorithms in [5] but it is hard to understand for beginners who have just started to learn Machine Learning. [6] is a special gift for beginners who want to learn about Support Vector Machine basically. In this article, I am going to introduce about SVM and a simplified version of the SMO by using Python code based on [4].
Background
In this article, we will consider a linear classifier for a binary classification problem with labels y (y ϵ [-1,1]) and features x. A SVM will compute a linear classifier (or a line) of the form:
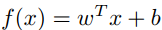
With f(x), we can predict y = 1 if f(x) ≥ 0 and y = -1 if f(x) < 0. And by solving the dual problem (Equation 12, 13 in [1] at the References section), f(x) can be expressed:

where αi (alpha i) is a Lagrange multiplier for solution and <x(i),x> called inner product of x(i) and x. A Python version of f(x) maybe look like this:
fXi = float(multiply(alphas,Y).T*(X*X[i,:].T)) + b
The Simplified SMO Algorithm
The simplified SMO algorithm takes two α parameters, αi and αj, and optimizes them. To do this, we iterate over all αi, i = 1, . . . m. If αi does not fulfill the Karush-Kuhn-Tucker conditions to within some numerical tolerance, we select αj at random from the remaining m − 1 α’s and optimize αi and αj. The following function is going to help us to select j randomly:
def selectJrandomly(i,m):
j=i
while (j==i):
j = int(random.uniform(0,m))
return j
If none of the α’s are changed after a few iterations over all the αi’s, then the algorithm terminates. We must also find bounds L and H:
- If y(i) != y(j), L = max(0, αj − αi), H = min(C, C + αj − αi)
- If y(i) = y(j), L = max(0, αi + αj − C), H = min(C, αi + αj)
Where C is a regularization parameter. Python code for the above is as follows:
if (Y[i] != Y[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
Now, we are going to find αj is given by:

Python code:
alphas[j] -= Y[j]*(Ei - Ej)/eta
Where:

Python code:
Ek = fXk - float(Y[k])
eta = 2.0 * X[i,:]*X[j,:].T - X[i,:]*X[i,:].T - X[j,:]*X[j,:].T
If this value ends up lying outside the bounds L and H, we must clip the value of αj to lie within this range:

The following function is going to help us to clip the value αj:
def clipAlphaJ(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
Finally, we can find the value for αi. This is given by:

where α(old)j is the value of αj before optimization. A version of Python code can look like this:
alphas[i] += Y[j]*Y[i]*(alphaJold - alphas[j])
After optimizing αi and αj, we select the threshold b:

where b1:

and b2:

Python code for b1 and b2:
b1 = b - Ei- Y[i]*(alphas[i]-alphaIold)*X[i,:]*X[i,:].T - Y[j]*(alphas[j]-alphaJold)*X[i,:]*X[j,:].T
b2 = b - Ej- Y[i]*(alphas[i]-alphaIold)*X[i,:]*X[j,:].T - Y[j]*(alphas[j]-alphaJold)*X[j,:]*X[j,:].T
Computing the W
After optimizing αi and αj, we can also compute w that is given:

The following function helps us to compute w from αi and αj:
def computeW(alphas, dataX, classY):
X = mat(dataX)
Y = mat(classY).T
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*Y[i],X[i,:].T)
return w
Predicted Class
We can predict which class a point belongs to from w and b:
def predictedClass(point, w, b):
p = mat(point)
f = p*w + b
if f > 0:
print(point," is belong to Class 1")
else:
print(point," is belong to Class -1")
The Python Function for the Simplified SMO Algorithm
And now, we can create a function (named simplifiedSMO) for the simplified SMO algorithm based on pseudo code in [4]:
Input
- C: regularization parameter
- tol: numerical tolerance
- max passes: max # of times to iterate over α’s without changing
- (x(1), y(1)), . . . , (x(m), y(m)): training data
Output
α : Lagrange multipliers for solution
b : threshold for solution
def simplifiedSMO(dataX, classY, C, tol, max_passes):
X = mat(dataX);
Y = mat(classY).T
m,n = shape(X)
b = 0;
alphas = mat(zeros((m,1)))
passes = 0
while (passes < max_passes):
num_changed_alphas = 0
for i in range(m):
fXi = float(multiply(alphas,Y).T*(X*X[i,:].T)) + b
Ei = fXi - float(Y[i])
if ((Y[i]*Ei < -tol) and (alphas[i] < C)) or ((Y[i]*Ei > tol)
and (alphas[i] > 0)):
j = selectJrandom(i,m)
fXj = float(multiply(alphas,Y).T*(X*X[j,:].T)) + b
Ej = fXj - float(Y[j])
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
if (Y[i] != Y[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H:
continue
eta = 2.0 * X[i,:]*X[j,:].T - X[i,:]*X[i,:].T - X[j,:]*X[j,:].T
if eta >= 0:
continue
alphas[j] -= Y[j]*(Ei - Ej)/eta
alphas[j] = clipAlphasJ(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001):
continue
alphas[i] += Y[j]*Y[i]*(alphaJold - alphas[j])
b1 = b - Ei- Y[i]*(alphas[i]-alphaIold)*X[i,:]*X[i,:].T -
Y[j]*(alphas[j]-alphaJold)*X[i,:]*X[j,:].T
b2 = b - Ej- Y[i]*(alphas[i]-alphaIold)*X[i,:]*X[j,:].T
- Y[j]*(alphas[j]-alphaJold)*X[j,:]*X[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
num_changed_alphas += 1
if (num_changed_alphas == 0): passes += 1
else: passes = 0
return b,alphas
Plotting the Linear Classifier
After having alpha, w and b, we can also plot the linear classifier (or a line). The following function is going to help us to do this:
def plotLinearClassifier(point, w, alphas, b, dataX, labelY):
shape(alphas[alphas>0])
Y = np.array(labelY)
X = np.array(dataX)
svmMat = []
alphaMat = []
for i in range(10):
alphaMat.append(alphas[i])
if alphas[i]>0.0:
svmMat.append(X[i])
svmPoints = np.array(svmMat)
alphasArr = np.array(alphaMat)
numofSVMs = shape(svmPoints)[0]
print("Number of SVM points: %d" % numofSVMs)
xSVM = []; ySVM = []
for i in range(numofSVMs):
xSVM.append(svmPoints[i,0])
ySVM.append(svmPoints[i,1])
n = shape(X)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelY[i])== 1:
xcord1.append(X[i,0])
ycord1.append(X[i,1])
else:
xcord2.append(X[i,0])
ycord2.append(X[i,1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
for j in range(0,len(xcord1)):
for l in range(numofSVMs):
if (xcord1[j]== xSVM[l]) and (ycord1[j]== ySVM[l]):
ax.annotate("SVM", (xcord1[j],ycord1[j]), (xcord1[j]+1,ycord1[j]+2),
arrowprops=dict(facecolor='black', shrink=0.005))
ax.scatter(xcord2, ycord2, s=30, c='green')
for k in range(0,len(xcord2)):
for l in range(numofSVMs):
if (xcord2[k]== xSVM[l]) and (ycord2[k]== ySVM[l]):
ax.annotate("SVM", (xcord2[k],ycord2[k]),(xcord2[k]-1,ycord2[k]+1),
arrowprops=dict(facecolor='black', shrink=0.005))
red_patch = mpatches.Patch(color='red', label='Class 1')
green_patch = mpatches.Patch(color='green', label='Class -1')
plt.legend(handles=[red_patch,green_patch])
x = []
y = []
for xfit in np.linspace(-3.0, 3.0):
x.append(xfit)
y.append(float((-w[0]/w[1])*xfit - b[0,0])/w[1])
ax.plot(x,y)
predictedClass(point,w,b)
p = mat(point)
ax.scatter(p[0,0], p[0,1], s=30, c='black', marker='s')
circle1=plt.Circle((p[0,0],p[0,1]),0.6, color='b', fill=False)
plt.gcf().gca().add_artist(circle1)
plt.show()
Using the Code
To run all of Python code above, we need to create three files:
- The myData.txt file contains training data:
-3 -2 0
-2 3 0
-1 -4 0
2 3 0
3 4 0
-1 9 1
2 14 1
1 17 1
3 12 1
0 8 1
In each row, the two first values are features and the third value is a label.
- The SimSMO.py file contains functions:
def loadDataSet(fileName):
dataX = []
labelY = []
fr = open(fileName)
for r in fr.readlines():
record = r.strip().split()
dataX.append([float(record[0]), float(record[1])])
labelY.append(float(record[2]))
return dataX, labelY
def selectJrandomly(i,m):
...
def clipAlphaJ(alphasj,H,L):
...
def simplifiedSMO(dataX, classY, C, tol, max_passes):
...
def computeW(alphas,dataX,classY):
...
def plotLinearClassifier(point, w, alphas, b, dataX, labelY):
...
def predictedClass(point, w, b):
...
- Finally, we need to create the testSVM.py file to test functions:
import SimSMO
X,Y = SimSMO.loadDataSet('myData.txt')
b,alphas = SimSMO.simplifiedSMO(X, Y, 0.6, 0.001, 40)
w = SimSMO.computeW(alphas,X,Y)
SimSMO.plotLinearClassifier([3,4], w, alphas, b, X, Y)
The result can look like this:
Number of SVM points: 3
[3, 4] is belong to Class -1
And:

Points of Interest
In this article, I only introduced the SVM basically and a simplified version of the SMO algorithm. If you want to use SVMs and the SMO in a real world application, you can discover more about them in documents below (or maybe more).
References
History
- 18th November, 2018: Initial version
