Introduction
Solving triangles means finding missing sides, angles and others measures. The form of calculation will depend on which sides or angles you already know.
The method that we will use is valid for the cases in which we know the measures of the three sides of the triangle (SSS).
For this, we will create a package in the GO language with all the structures and methods to perform the calculations.
Background
See the generic triangle ABC below:

From the information of the measures of its sides a, b and c, we can calculate the following elements:
- Perimeter ⇒ A perimeter is a path that surrounds a 2D shape. In the case of the triangle is given by the sum of its sides:

- Semiperimeter ⇒ The semiperimeter (S) is defined as the half the length of a perimeter:
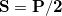
- Area ⇒ The area of the triangle can be obtained through the Heron's formula (sometimes called Hero's formula):

- Angles ⇒ We can calculate the angles of the triangle using the Law of Cosines:

- Heights ⇒ The height of a triangle is its highest altitude relative to a specific side (base). Therefore, each triangle has three heights (
Ha, Hb and Hc) that can be easily calculated through their areas:
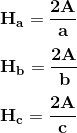
- Medians ⇒ A median is a line segment joining a vertex with the mid-point of the opposite side.
Every triangle has 3 medians. Here are the formulas for calculating the lengths of medians (ma, m and mc):
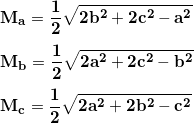
- Inscribed and circumscribed circumference ⇒ Every triangle can be inscribed and circumscribed on a circumference. To calculate the radii measurements of these circles, the
InRadius (Ri) and CincumRadius (Rc), we use the following formulas:

- Type of triangles ⇒ Triangles are classified depending on relative sizes of their elements.
As regards their sides, triangles may be:
- Scalene (all sides are different)
- Isosceles (two sides are equal)
- Equilateral (all three sides are equal)
And as regards their angles, triangles may be:
- Acute (all angles are acute)
- Right (one angle is right)
- Obtuse (one angle is obtuse)
Using the Code
The GO language is strict about the names, formats and file locations.
Files with source codes should be organized into packages that should be placed under a parent folder named src, what is our workspace folder.
Other important points that should be observed for a better understanding:
- Package names must be written in lower case.
- The following environment variables must be set in the operating system:
- GOPATH ⇒The workspace folder address
- GOROOT ⇒ If you chose a directory other than c:\Go, you must set the
GOROOT environment variable to your chosen path. PATH ⇒ Add the bin subdirectory of your Go root (for example, c:\Go\bin) to your PATH environment variable.
For this article, we have created the following files:
Triangle.go ⇒ Representation of a triangle with the necessary structures and methods. This file will stay in the folder: go/src/math/geometry/polygon
TriangleTest.go ⇒ Example of using the polygon package in which we created a triangle and performed some tests of the calculations. This file will stay in the folder: go/src/math/geometry
Let's go to the GO code...
Triangle.go
package polygon
import "math"
type Triangle struct {
a float64 b float64 c float64 isTriangle bool }
func (self Triangle) Sides() (float64, float64, float64) {
return self.a, self.b, self.c
}
func (self *Triangle) SetSides(a, b, c float64) bool {
self.isTriangle = false
self.a = a
self.b = b
self.c = c
if self.a <= (self.b+self.c) && self.b <= (self.a+self.c) && self.c <= (self.a+self.b) {
self.isTriangle = true
}
return self.isTriangle
}
func (self Triangle) IsTriangle() bool {
return self.isTriangle
}
func (self Triangle) Perimeter() float64 {
perimeter := 0.0
if self.IsTriangle() {
perimeter = (self.a + self.b + self.c)
}
return perimeter
}
func (self Triangle) Semiperimeter() float64 {
semiperimeter := 0.0
if self.IsTriangle() {
semiperimeter = self.Perimeter() / 2
}
return semiperimeter
}
func (self Triangle) Area() float64 {
area := 0.0
s := self.Semiperimeter()
if self.IsTriangle() {
area = math.Sqrt(s * ((s - self.a) * (s - self.b) * (s - self.c)))
}
return area
}
func (self Triangle) InRadius() float64 {
inRadius := 0.0
semiperimeter := self.Semiperimeter()
area := self.Area()
if self.IsTriangle() {
inRadius = area / semiperimeter
}
return inRadius
}
func (self Triangle) CircumRadius() float64 {
circumRadius := 0.0
alpha, _, _ := self.Angles()
if self.IsTriangle() {
circumRadius = self.a / (2.0 * math.Abs(math.Sin(rad2deg(alpha))))
}
return circumRadius
}
func (self Triangle) TypeBySide() string {
bySide := "None"
if self.IsTriangle() {
if self.a == self.b && self.b == self.c {
bySide = "Equilateral"
} else if self.a == self.b || self.b == self.c || self.a == self.c {
bySide = "Isosceles"
} else {
bySide = "Scalene"
}
}
return bySide
}
func (self Triangle) TypeByAngle() string {
alpha, beta, gamma := self.Angles()
byAngle := "None"
if self.IsTriangle() {
if alpha == 90 || beta == 90 || gamma == 90 {
byAngle = "Right"
} else if alpha > 90 || beta > 90 || gamma > 90 {
byAngle = "Obtuse"
} else {
byAngle = "Acute"
}
}
return byAngle
}
func (self Triangle) Angles() (float64, float64, float64) {
alpha := 0.0
beta := 0.0
gamma := 0.0
if self.IsTriangle() {
alpha = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.c, 2.0)
- math.Pow(self.a, 2.0)) / (2.0 * self.b * self.c))
beta = math.Acos((math.Pow(self.c, 2.0) + math.Pow(self.a, 2.0)
- math.Pow(self.b, 2.0)) / (2.0 * self.c * self.a))
gamma = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.a, 2.0)
- math.Pow(self.c, 2.0)) / (2.0 * self.a * self.b))
}
alpha = rad2deg(alpha)
beta = rad2deg(beta)
gamma = 180 - (alpha + beta)
return alpha, beta, gamma
}
func (self Triangle) Heights() (float64, float64, float64) {
area := self.Area()
aHeight := 0.0
bHeight := 0.0
cHeight := 0.0
if self.IsTriangle() {
aHeight = 2.0 * area / self.a
bHeight = 2.0 * area / self.b
cHeight = 2.0 * area / self.c
}
return aHeight, bHeight, cHeight
}
func (self Triangle) Medians() (float64, float64, float64) {
aMedian := 0.0
bMedian := 0.0
cMedian := 0.0
if self.IsTriangle() {
aMedian = math.Sqrt(2.0*math.Pow(self.b, 2.0)+
2.0*math.Pow(self.c, 2.0)-math.Pow(self.a, 2.0)) / 2.0
bMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
2.0*math.Pow(self.c, 2.0)-math.Pow(self.b, 2.0)) / 2.0
cMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
2.0*math.Pow(self.b, 2.0)-math.Pow(self.c, 2.0)) / 2.0
}
return aMedian, bMedian, cMedian
}
func rad2deg(rad float64) float64 {
return rad * 180 / math.Pi
}
TriangleTest.go
package main
import (
"fmt"
"math/geometry/polygon"
)
func main() {
fmt.Printf("\nTriangle Calculations\n\n")
var a, b, c float64
fmt.Printf("Enter the size of the a side: ")
fmt.Scan(&a)
fmt.Printf("Enter the size of the b side: ")
fmt.Scan(&b)
fmt.Printf("Enter the size of the c side: ")
fmt.Scan(&c)
tri := new(polygon.Triangle)
tri.SetSides(a, b, c)
fmt.Printf("\nResults:\n")
if tri.IsTriangle() {
fmt.Printf("Type by side = %s\n", tri.TypeBySide())
fmt.Printf("Type by angle = %s\n", tri.TypeByAngle())
fmt.Printf("Perimeter = %f\n", tri.Perimeter())
fmt.Printf("Semiperimeter = %f\n", tri.Semiperimeter())
fmt.Printf("Area = %f\n", tri.Area())
fmt.Printf("Radius of the circumscribed circle = %f\n", tri.CircumRadius())
fmt.Printf("Radius of the inscribed circle = %f\n", tri.InRadius())
alfa, beta, gama := tri.Angles()
fmt.Printf("Alfa, Beta, Gama Angles = %f, %f, %f \n", alfa, beta, gama)
fmt.Printf("Sum of the Angles = %f \n", (alfa + beta + gama))
aHeight, bHeight, cHeight := tri.Heights()
fmt.Printf("Heights a, b and c = %f, %f, %f \n", aHeight, bHeight, cHeight)
aMedian, bMedian, cMedian := tri.Medians()
fmt.Printf("Medians a, b and c = %f, %f, %f \n", aMedian, bMedian, cMedian)
} else {
fmt.Printf("These sides do not form a triangle!\n\n")
}
}
Points of Interest
General
- Variable names and methods written with the first capital letter have global visibility (
public); - Variable names and methods written with the first lowercase letter have local visibility (
private); - Just like in Lua language, a function in GO can return more than one value. This is not mathematically correct, but it is very practical. In most cases, this feature is used to return error codes, which is great.
Triangle.go
Go does not have pass-by-reference function call semantics. Instead, we use pass-by-pointer when needed, like in the SetSides method;- In
Go, there are no classes or constructors. Instead, we use Struct Types and Setter Methods; - The
Triangle structure has four variables:
- Three float variables (
a, b, c) to represent the dimensions of the sides of the triangle. - A boolean variable (
isTriangle) that indicates whether these three sides are valid to form a triangle.
Note that these variables start with lowercase letters, which means they have the local visibility scope. For an external routine to access these variables, there are the accessor methods Sides (Getter) and SetSides (Setter).
All methods test this variable before performing the calculations.
- The
SetSides method receives the parameters by reference with the use of the dereferencing operator. - The
rad2deg function is a private method and therefore cannot be accessed externally.
TriangleTest.go
- The
main function in the package “main” will be the entry point of our executable program. - In the
main method, we use new that is a built-in function that allocates memory for the Triangle type and returns its address.
A Word About Precision
Calculations involving floating-point values are not accurate. The float64 type in GO is very precise according to our tests, but even so, some care should be taken.
In the case of the angles calculation, for example, we use a trick to ensure that its sum will always be 180 degrees.
In addition, some rare types of triangles can produce unexpected results. Are they:
- A degenerate Triangle, a triangle with collinear vertices and zero area. This case will result in an invalid triangle in our algorithm and the calculations will not be performed;
- A Needle-like Triangle, a triangle in which two sides add little more than the third (nearly a straight segment). In such cases, our calculations may result in precision errors.
Next Steps
Some enhancements that can be done in the future:
- Allow the calculations of the triangles not only through their sides (SSS), but through other combinations
- Create a polygon interface to perform calculations with other geometric shapes
- Improve calculations by predicting cases of needle-triangles
Know More...
Triangles
GO Language
History
- 2018-December-11 - Added the precision section
Final Words
Thanks for reading!
Find me on GitHub for more mathematical algorithms.
