Solving Triangles, an Approach with GO Language

• Download source - 2.6 KB

Introduction

Solving triangles means finding missing sides, angles and others measures. The form of calculation will depend on which sides or angles you already know.
The method that we will use is valid for the cases in which we know the measures of the three sides of the triangle (SSS).
For this, we will create a package in the GO language with all the structures and methods to perform the calculations.

Background

See the generic triangle ABC below:

From the information of the measures of its sides a, b and c, we can calculate the following elements:

1. Perimeter ⇒ A perimeter is a path that surrounds a 2D shape. In the case of the triangle is given by the sum of its sides:

   

2. Semiperimeter ⇒ The semiperimeter (S) is defined as the half the length of a perimeter:

   

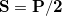
3. Area ⇒ The area of the triangle can be obtained through the Heron's formula (sometimes called Hero's formula):

   

4. Angles ⇒ We can calculate the angles of the triangle using the Law of Cosines:

   

5. Heights ⇒ The height of a triangle is its highest altitude relative to a specific side (base). Therefore, each triangle has three heights (Ha, Hb and Hc) that can be easily calculated through their areas:

   

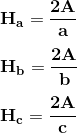
6. Medians ⇒ A median is a line segment joining a vertex with the mid-point of the opposite side.

   Every triangle has 3 medians. Here are the formulas for calculating the lengths of medians (m_a, m and m_c):

   

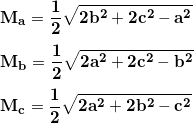
7. Inscribed and circumscribed circumference ⇒ Every triangle can be inscribed and circumscribed on a circumference. To calculate the radii measurements of these circles, the InRadius (Ri) and CincumRadius (Rc), we use the following formulas:

   

8. Type of triangles ⇒ Triangles are classified depending on relative sizes of their elements.

   As regards their sides, triangles may be:

   • Scalene (all sides are different)
   • Isosceles (two sides are equal)
   • Equilateral (all three sides are equal)

   And as regards their angles, triangles may be:

   • Acute (all angles are acute)
   • Right (one angle is right)
   • Obtuse (one angle is obtuse)

Using the Code

The GO language is strict about the names, formats and file locations.
Files with source codes should be organized into packages that should be placed under a parent folder named src, what is our workspace folder.

Other important points that should be observed for a better understanding:

• Package names must be written in lower case.
• The following environment variables must be set in the operating system:
  • GOPATH ⇒The workspace folder address
  • GOROOT ⇒ If you chose a directory other than c:\Go, you must set the GOROOT environment variable to your chosen path.
  • PATH ⇒ Add the bin subdirectory of your Go root (for example, c:\Go\bin) to your PATH environment variable.

For this article, we have created the following files:

Triangle.go ⇒ Representation of a triangle with the necessary structures and methods. This file will stay in the folder: go/src/math/geometry/polygon

TriangleTest.go ⇒ Example of using the polygon package in which we created a triangle and performed some tests of the calculations. This file will stay in the folder: go/src/math/geometry

Let's go to the GO code...

Triangle.go

/*

Triangle.go
Calculations with triangles

Language: GO

2018, Jose Cintra
email: josecintra@josecintra.com

*/

package polygon

import "math"

type Triangle struct {
	a          float64 // Size of A Side
	b          float64 // Size of B Side
	c          float64 // Size of C Side
	isTriangle bool    // These sides are valid for a triangle?
}

// Getter for the sides of the triangle
func (self Triangle) Sides() (float64, float64, float64) {
	return self.a, self.b, self.c
}

// Setter for the sides of the triangle
func (self *Triangle) SetSides(a, b, c float64) bool {
	self.isTriangle = false
	self.a = a
	self.b = b
	self.c = c
	if self.a <= (self.b+self.c) && self.b <= (self.a+self.c) && self.c <= (self.a+self.b) {
		self.isTriangle = true
	}
	return self.isTriangle
}

// These sides are valid for a triangle? (Getter)
func (self Triangle) IsTriangle() bool {
	return self.isTriangle
}

// Calculates the perimeter
func (self Triangle) Perimeter() float64 {
	perimeter := 0.0
	if self.IsTriangle() {
		perimeter = (self.a + self.b + self.c)
	}
	return perimeter
}

// Calculates the semiperimeter
func (self Triangle) Semiperimeter() float64 {
	semiperimeter := 0.0
	if self.IsTriangle() {
		semiperimeter = self.Perimeter() / 2
	}
	return semiperimeter
}

// Calculates the area of the triangle through Heron's Formula
func (self Triangle) Area() float64 {
	area := 0.0
	s := self.Semiperimeter()
	if self.IsTriangle() {
		area = math.Sqrt(s * ((s - self.a) * (s - self.b) * (s - self.c)))
	}
	return area
}

// Calculates the radius of the inscribed circle
func (self Triangle) InRadius() float64 {
	inRadius := 0.0
	semiperimeter := self.Semiperimeter()
	area := self.Area()
	if self.IsTriangle() {
		inRadius = area / semiperimeter
	}
	return inRadius
}

// Calculates the radius of the circumscribed circle
func (self Triangle) CircumRadius() float64 {
	circumRadius := 0.0
	alpha, _, _ := self.Angles()
	if self.IsTriangle() {
		circumRadius = self.a / (2.0 * math.Abs(math.Sin(rad2deg(alpha))))
	}
	return circumRadius
}

// Gets the triangle type according to its sides
func (self Triangle) TypeBySide() string {
	bySide := "None"
	if self.IsTriangle() {
		if self.a == self.b && self.b == self.c {
			bySide = "Equilateral"
		} else if self.a == self.b || self.b == self.c || self.a == self.c {
			bySide = "Isosceles"
		} else {
			bySide = "Scalene"
		}
	}
	return bySide
}

// Gets the type of the triangle according to its angles
func (self Triangle) TypeByAngle() string {
	alpha, beta, gamma := self.Angles()
	byAngle := "None"
	if self.IsTriangle() {
		if alpha == 90 || beta == 90 || gamma == 90 {
			byAngle = "Right"
		} else if alpha > 90 || beta > 90 || gamma > 90 {
			byAngle = "Obtuse"
		} else {
			byAngle = "Acute"
		}
	}
	return byAngle
}

// Calculates the angles of the triangle through the law of cosines
func (self Triangle) Angles() (float64, float64, float64) {
	alpha := 0.0
	beta := 0.0
	gamma := 0.0
	if self.IsTriangle() {
		alpha = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.c, 2.0) 
		- math.Pow(self.a, 2.0)) / (2.0 * self.b * self.c))
		beta = math.Acos((math.Pow(self.c, 2.0) + math.Pow(self.a, 2.0) 
		- math.Pow(self.b, 2.0)) / (2.0 * self.c * self.a))
		gamma = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.a, 2.0) 
		- math.Pow(self.c, 2.0)) / (2.0 * self.a * self.b))
	}
	alpha = rad2deg(alpha)
	beta = rad2deg(beta)
	gamma = 180 - (alpha + beta)
	return alpha, beta, gamma
}

// Calculates the heights of the triangle using the area formula
func (self Triangle) Heights() (float64, float64, float64) {
	area := self.Area()
	aHeight := 0.0
	bHeight := 0.0
	cHeight := 0.0
	if self.IsTriangle() {
		aHeight = 2.0 * area / self.a
		bHeight = 2.0 * area / self.b
		cHeight = 2.0 * area / self.c
	}
	return aHeight, bHeight, cHeight
}

// Calculates the Medians of the triangle
func (self Triangle) Medians() (float64, float64, float64) {
	aMedian := 0.0
	bMedian := 0.0
	cMedian := 0.0
	if self.IsTriangle() {
		aMedian = math.Sqrt(2.0*math.Pow(self.b, 2.0)+
		2.0*math.Pow(self.c, 2.0)-math.Pow(self.a, 2.0)) / 2.0
		bMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
		2.0*math.Pow(self.c, 2.0)-math.Pow(self.b, 2.0)) / 2.0
		cMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
		2.0*math.Pow(self.b, 2.0)-math.Pow(self.c, 2.0)) / 2.0
	}
	return aMedian, bMedian, cMedian
}

// Convert from radians to degree
func rad2deg(rad float64) float64 {
	return rad * 180 / math.Pi
}

TriangleTest.go

/*
TriangleTest
Test for the Triangle Package

Language: GO

2018, Jose Cintra
email: josecintra@josecintra.com
*/

package main

import (
	"fmt"
	"math/geometry/polygon"
)

func main() {
	fmt.Printf("\nTriangle Calculations\n\n")
	// Data entry
	var a, b, c float64
	fmt.Printf("Enter the size of the a side: ")
	fmt.Scan(&a)
	fmt.Printf("Enter the size of the b side: ")
	fmt.Scan(&b)
	fmt.Printf("Enter the size of the c side: ")
	fmt.Scan(&c)

	// Triangle object
	tri := new(polygon.Triangle)
	tri.SetSides(a, b, c)

	// Print the calculations
	fmt.Printf("\nResults:\n")
	if tri.IsTriangle() {
		fmt.Printf("Type by side = %s\n", tri.TypeBySide())
		fmt.Printf("Type by angle = %s\n", tri.TypeByAngle())
		fmt.Printf("Perimeter = %f\n", tri.Perimeter())
		fmt.Printf("Semiperimeter = %f\n", tri.Semiperimeter())
		fmt.Printf("Area = %f\n", tri.Area())
		fmt.Printf("Radius of the circumscribed circle = %f\n", tri.CircumRadius())
		fmt.Printf("Radius of the inscribed circle = %f\n", tri.InRadius())
		alfa, beta, gama := tri.Angles()
		fmt.Printf("Alfa, Beta, Gama Angles = %f, %f, %f \n", alfa, beta, gama)
		fmt.Printf("Sum of the Angles = %f \n", (alfa + beta + gama))
		aHeight, bHeight, cHeight := tri.Heights()
		fmt.Printf("Heights a, b and c = %f, %f, %f \n", aHeight, bHeight, cHeight)
		aMedian, bMedian, cMedian := tri.Medians()
		fmt.Printf("Medians a, b and c = %f, %f, %f \n", aMedian, bMedian, cMedian)
	} else {
		fmt.Printf("These sides do not form a triangle!\n\n")
	}
}

Points of Interest

General

• Variable names and methods written with the first capital letter have global visibility (public);
• Variable names and methods written with the first lowercase letter have local visibility (private);
• Just like in Lua language, a function in GO can return more than one value. This is not mathematically correct, but it is very practical. In most cases, this feature is used to return error codes, which is great.

Triangle.go

• Go does not have pass-by-reference function call semantics. Instead, we use pass-by-pointer when needed, like in the SetSides method;
• In Go, there are no classes or constructors. Instead, we use Struct Types and Setter Methods;
• The Triangle structure has four variables:
  • Three float variables (a, b, c) to represent the dimensions of the sides of the triangle.
  • A boolean variable (isTriangle) that indicates whether these three sides are valid to form a triangle.

    Note that these variables start with lowercase letters, which means they have the local visibility scope. For an external routine to access these variables, there are the accessor methods Sides (Getter) and SetSides (Setter).
    All methods test this variable before performing the calculations.

• The SetSides method receives the parameters by reference with the use of the dereferencing operator.
• The rad2deg function is a private method and therefore cannot be accessed externally.

TriangleTest.go

• The main function in the package “main” will be the entry point of our executable program.
• In the main method, we use new that is a built-in function that allocates memory for the Triangle type and returns its address.

A Word About Precision

Calculations involving floating-point values are not accurate. The float64 type in GO is very precise according to our tests, but even so, some care should be taken.
In the case of the angles calculation, for example, we use a trick to ensure that its sum will always be 180 degrees.

In addition, some rare types of triangles can produce unexpected results. Are they:

• A degenerate Triangle, a triangle with collinear vertices and zero area. This case will result in an invalid triangle in our algorithm and the calculations will not be performed;
• A Needle-like Triangle, a triangle in which two sides add little more than the third (nearly a straight segment). In such cases, our calculations may result in precision errors.

Next Steps

Some enhancements that can be done in the future:

• Allow the calculations of the triangles not only through their sides (SSS), but through other combinations
• Create a polygon interface to perform calculations with other geometric shapes
• Improve calculations by predicting cases of needle-triangles

Know More...

Triangles

• Triangle Properties and Types
• Solving Triangles
• Triangle Calculator

GO Language

• GO Succintly
• Effective GO

History

• 2018-December-11 - Added the precision section

Final Words

Thanks for reading!
Find me on GitHub for more mathematical algorithms.