Introduction
Since .NET was first released, I've been itching to write my own collection of data structures and algorithms. This is an attempt at providing a reusable, generic collection of data structures and algorithms for use in .NET 2.0 and beyond. This article will not provide all the details and full descriptions of the inner workings of these collections and algorithms - rather, it will provide links to resources available on the web (there is no sense in trying to beat Wikipedia) and provide points of interest on this specific implementation.
Background
The .NET framework has grown into a very rich framework indeed. It provides numerous well thought-out interfaces and classes, but omits a lot of data structures and algorithms that are of significance in the field of Computer Science. This library attempts to provide this missing functionality and extend the .NET framework.
Overview
The following data structures and algorithms are currently implemented :
| New Data Structures | Extended Data Structures | Sorting Algorithms | Graph Algorithms |
Association<TKey, TValue> | VisitableHashTable<TKey, TValue> | Bubble Sort | Djikstra's Single Source Shortest Path algorithm |
Bag<T> | VisitableLinkedList<T> | Bucket Sort | Prim's Minimal Spanning Tree Algorithm |
BinaryTree<T> | VisitableList<T> | Cocktail Sort | |
BinarySearchTree<TKey, TValue> | VisitableQueue<T> | Comb Sort | Math Algorithms |
Deque<T> | VisitableStack<T> | Gnome Sort | Fibonacci number generation. |
GeneralTree<T> | | Heap Sort | Euclid's Algorithm |
Graph<T> | | Insertion Sort | |
Heap<T> | | Merge Sort | |
Matrix | | Odd-Even Transport Sort | |
PascalSet | | Quick Sort | |
PriorityQueue<T> | | Selection Sort | |
SkipList<TKey, TValue> | | Shaker Sort | |
SortedList<T> | | Shell Sort | |
SortedList<T> | | Shell Sort | |
RedBlackTree<T> | | | |
ReadOnlyPropertyCollection <T, TProperty> | | | |
ObjectMatrix<T> | | | |
HashList<TKey, TValue> | | | |
Using the code
Data structures provided
The IVisitableCollection interface
public interface IVisitable<T>
{
void Accept(IVisitor<T> visitor);
}
public interface IVisitableCollection<T> :
ICollection<T>, IEnumerable<T>,
IEnumerable, IComparable, IVisitable<T>
{
bool IsEmpty { get; }
bool IsFixedSize { get; }
bool IsFull { get; }
}
The Visitor pattern is probably one of the most used (and many say overrated) patterns in Computer Science. The IVisitableCollection<T> interface provides an interface for any collection to accept visitors - thus keeping the action performed on objects separate from the implementation of the specific data structure. For more information on Visitors, see the IVisitor<T> interface.
When the Accept method is called, the collection must enumerate though all the objects contained in it and call the Visit method of the visitor on each of those. The IsEmpty and IsFull return an boolean value indicating whether the current instance is empty or full, respectively (surprise, surprise). The IsFull method only applies to fixed size collections, and indicates that a collection does not dynamically grow as items get added to it.
Another interface called IVisitableDictionary<T> is used for representing dictionary based collections, also implementing the IVisitable<T> interface.
Association
public class Association<TKey, TValue>
{
public Association(TKey key, TValue value);
public KeyValuePair<TKey, TValue> ToKeyValuePair();
public TKey Key { get; set; }
public TValue Value { get; set; }
}
A class cloning the functionality of the standard KeyValuePair<TKey, TValue>, but with added setters on the Key and Value properties. The Association class is used primarily in the SortedList data structure, where it's necessary to keep a key-value relationship between the priority and the value of an item.
Bag
public class Bag<T> : IVisitableCollection<T>, IBag<T>
{
public void Accept(IVisitor<KeyValuePair<T, int>> visitor);
public void Add(T item, int amount);
public Bag<T> Difference(Bag<T> bag);
public IEnumerator<KeyValuePair<T, int>> GetCountEnumerator();
public IEnumerator<T> GetEnumerator();
public Bag<T> Intersection(Bag<T> bag);
public bool IsEqual(Bag<T> bag);
public static Bag<T> operator +(Bag<T> b1, Bag<T> b2);
public static Bag<T> operator *(Bag<T> b1, Bag<T> b2);
public static Bag<T> operator -(Bag<T> b1, Bag<T> b2);
public bool Remove(T item, int max);
public Bag<T> Union(Bag<T> bag);
public int this[T item] { get; }
}
A Bag is a data structure containing any amount of elements. It differs from a set in that it allows multiple instances of items to be contained in the collection, and is thus more geared towards "counting" items. The Bag data structure contained in this library is implemented by using a Dictionary<T, int> data structure, keeping a reference to the number of items contained in the Bag.
The Bag class is implemented using a Dictionary<KeyType, int> object where the object gets hashed with a counter representing the amount of specific items contained in the Bag. The standard operations are implemented:
- Intersection - Returns a Bag containing items contained in both Bags.
- Union - Returns a Bag with all the items in both Bags.
- Difference - "Subtract" one Bag from another. This operation subtracts the number of items contained in the other Bag on the applied Bag.
BinaryTree
public class BinaryTree<T> : IVisitableCollection<T>, ITree<T>
{
public void Add(BinaryTree<T> subtree);
public virtual void breadthFirstTraversal(IVisitor<T> visitor);
public virtual void
DepthFirstTraversal(OrderedVisitor<T> orderedVisitor);
public BinaryTree<T> GetChild(int index);
public bool Remove(BinaryTree<T> child);
public virtual void RemoveLeft();
public virtual void RemoveRight();
public virtual T Data { get; set; }
public int Degree { get; }
public virtual int Height { get; }
public virtual bool IsLeafNode { get; }
public BinaryTree<T> this[int i] { get; }
public virtual BinaryTree<T> Left { get; set; }
public virtual BinaryTree<T> Right { get; set; }
}
A binary tree is a special kind of tree where each node in the tree has a maximum of two child nodes. The BinaryTree<T> class contains pointers to a maximum of two child nodes. The BreadthFirstTraversal and DepthFirstTraversal methods provide the specified access to given Visitors. Depth-first traversal can be done in three ways: in-order, post-order, or pre-order, where in-order is only applicable to binary trees.
The Height property works by recursively counting the number of levels in this binary tree and below. Since each child of a BinaryTree is a BinaryTree itself, each child has its own height.
[More information on Binary Trees]
Binary Search Tree
public class BinarySearchTree<TKey, TValue> :
IVisitableDictionary<TKey, TValue>,
IDictionary<TKey, TValue>,
IVisitableCollection<KeyValuePair<TKey, TValue>>
{
public void Accept(IVisitor<KeyValuePair<TKey, TValue>> visitor);
public void Add(KeyValuePair<TKey, TValue> item);
public void Add(TKey key, TValue value);
public int CompareTo(object obj);
public bool Contains(KeyValuePair<TKey, TValue> item);
public bool ContainsKey(TKey key);
public void CopyTo(KeyValuePair<TKey, TValue>[] array, int arrayIndex);
public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator();
public IEnumerator<KeyValuePair<TKey, TValue>> GetSortedEnumerator();
public bool Remove(KeyValuePair<TKey, TValue> item);
public bool Remove(TKey key);
public bool TryGetValue(TKey key, out TValue value);
public IComparer<TKey> Comparer { get; }
public int Count { get; }
public bool IsEmpty { get; }
public bool IsFixedSize { get; }
public bool IsFull { get; }
public bool IsReadOnly { get; }
public TValue this[TKey key] { get; set; }
public ICollection<TKey> Keys { get; }
public KeyValuePair<TKey, TValue> Max { get; }
public KeyValuePair<TKey, TValue> Min { get; }
public ICollection<TValue> Values { get; }
}
A Binary Search tree is a search data structure that takes the form of a Binary Tree. It's inner workings are simple : items less than the parent node are placed in the left subtree, and items larger in the right subtree. This allows for quick searching of items by elimating more items on each level. One of it's worst cases, however, is adding items in sequential order - O(n) comparisons are necessary in the worst case. However, because of it's simplicity it's a suitable search data structure for cases where the input will be randomized. Where randomized data can not be ensured, the use of a balanced search tree (like a Red Black Tree) is recommended.
[More information on Binary Search Trees]
Deque
public sealed class Deque<T> : IVisitableCollection<T>, IDeque<T>
{
public T DequeueHead();
public T DequeueTail();
public void EnqueueHead(T obj);
public void EnqueueTail(T obj);
public T Head { get; }
public T Tail { get; }
}
The Deque (or double-ended queue) data structure is similar to a Queue data structure except that it can enqueue or dequeue to either the head or the tail of the current queue. The Deque is implemented as a Linked List, providing easy access to the front and the back of the list.
[More information on Deques]
GeneralTree
public class GeneralTree<T> : IVisitableCollection<T>, ITree<T>
{
public void Add(GeneralTree<T> child);
public void breadthFirstTraversal(Visitor<T> visitor);
public void DepthFirstTraversal(OrderedVisitor<T> orderedVisitor);
public GeneralTree<T> GetChild(int index);
public bool Remove(GeneralTree<T> child);
public void RemoveAt(int index);
public void Sort(ISorter<GeneralTree<GeneralTree<T>>> sorter);
public void Sort(ISorter<GeneralTree<GeneralTree<T>>> sorter,
IComparer<GeneralTree<T>> comparer);
public void Sort(ISorter<GeneralTree<GeneralTree<T>>> sorter,
Comparison<GeneralTree<T>> comparison);
public T Data { get; }
public int Degree { get; }
public int Height { get; }
public virtual bool IsLeafNode { get; }
public GeneralTree<T> this[int i] { get; }
public GeneralTree<T>[] Ancestors { get; }
public GeneralTree<T> Parent { get; }
}
General Trees is the most generic kind of tree data structure. It allows for any number of child nodes for a given node (including zero nodes, which makes it a leaf node). The GeneralTree<T> class, like the BinaryTree<T> class, allows for breadth-first traversal and depth-first traversal for Visitors.
The GeneralTree is implemented with a list for keeping track of children (also of type GeneralTree). The Height property works similar to the binary tree's Height property - it recursively counts the number of levels down the tree.
[More information on tree data structures]
Graph
The Graph data structure consists of three parts :
- A
Vertex<T> class that represents a node in the graph. - An
Edge<T> class that forms a link between two vertices. - A
Graph<T> class that represents the collection of edges and vertices.
Vertex<T>
public class Vertex<T>
{
public Edge<T> GetEmanatingEdgeTo(Vertex<T> toVertex);
public Edge<T> GetIncidentEdgeWith(Vertex<T> toVertex);
public bool HasEmanatingEdgeTo(Vertex<T> toVertex);
public bool HasIncidentEdgeWith(Vertex<T> fromVertex);
public T Data { get; set; }
public int Degree { get; }
public IEnumerator<Edge<T>> EmanatingEdges { get; }
public IEnumerator<Edge<T>> IncidentEdges { get; }
public int IncidentEdgesCount { get; }
}
The Vertex<T> class represents a node in the graph. It keeps a list of edges (added by the graph) emanating from it (directed to the other vertex), and incident edges. These lists can be accessed by the EmanatingEdges and IncidentEdges properties. A data item is associated with the vertex to differentiate it from other vertices.
Edge<T>
public class Edge<T>
{
public Vertex<T> GetPartnerVertex(Vertex<T> vertex);
public Vertex<T> FromVertex { get; }
public bool IsDirected { get; }
public Vertex<T> ToVertex { get; }
public double Weight { get; }
}
The Edge<T> class represents an edge between two vertices in a graph, which can be either directed or undirected depending on the graph type. Edges can be weighted, i.e., a value can be assigned to an edge to represent its payload or distance between the two vertices. The GetPartnerVertex method, given a vertex contained in the edge, returns the other vertex in the relationship.
Graph<T>
public class Graph<T> : IVisitableCollection<T>
{
public void AddEdge(Edge<T> edge);
public Edge<T> AddEdge(Vertex<T> from, Vertex<T> to);
public Edge<T> AddEdge(Vertex<T> from, Vertex<T> to, double weight);
public void AddVertex(Vertex<T> vertex);
public Vertex<T> AddVertex(T item);
public void BreadthFirstTraversal(IVisitor<Vertex<T>> visitor,
Vertex<T> startVertex);
public bool ContainsEdge(Edge<T> edge);
public bool ContainsEdge(Vertex<T> from, Vertex<T> to);
public bool ContainsEdge(T fromValue, T toValue);
public bool ContainsVertex(Vertex<T> vertex);
public bool ContainsVertex(T item);
public void DepthFirstTraversal(OrderedVisitor<Vertex<T>> visitor,
Vertex<T> startVertex);
public Edge<T> GetEdge(Vertex<T> from, Vertex<T> to);
public bool RemoveEdge(Edge<T> edge);
public bool RemoveEdge(Vertex<T> from, Vertex<T> to);
public bool RemoveVertex(Vertex<T> vertex);
public bool RemoveVertex(T item);
public int EdgeCount { get; }
public IEnumerator<Edge<T>> Edges { get; }
public bool IsDirected { get; }
public bool IsStronglyConnected { get; }
public bool IsWeaklyConnected { get; }
public int VertexCount { get; }
public IEnumerator<Vertex<T>> Vertices { get; }
}
The Graph<T> class is a container of vertices and edges. All add and remove operations are performed by the graph. The standard add, remove, and get operations are implemented. Also implemented is a DepthFirstTraversal and a BreadthFirstTraversal similar to the tree data structures, except that they require a start vertex since a graph has no root.
The IsStronglyConnected and IsWeaklyConnected tests for connectivity in a graph. Weak connectedness ensures that there is an undirected edge between every vertex in the graph. In other words, all vertices are reachable from every other vertex. Note that for a directed graph, the algorithm represents directed edges as undirected edges. Testing if a graph is strongly connected entails ensuring that each vertex is reachable from every other vertex, and is only available on directed graphs.
[More information on graphs]
HashList
public sealed class HashList<TKey, TValue> :
VisitableHashtable<TKey, IList<TValue>>
{
public void Add(TKey key, ICollection<TValue> values);
public void Add(TKey key, TValue value);
public IEnumerator<TValue> GetValueEnumerator();
public bool Remove(TValue item);
public bool Remove(TKey key, TValue item);
public void RemoveAll(TValue item);
public int KeyCount { get; }
public int ValueCount { get; }
}
A HashList (or multi-dictionary) is a HashTable than can store multiple value for a specific key. It's built on the standard Dictionary class, and performs the same functions as the Dictionary<TKey, IList<TValue>> class, with prettier syntax.
[More information on Hash Lists]
Heap
public class Heap<T> : IVisitableCollection<T>, IHeap<T>
{
public override void Add(T item);
public T RemoveSmallestItem();
public T SmallestItem { get; }
}
The Heap data structure is a tree structure with a special property: either the smallest item (a Min-Heap) or the largest item (a Max-Heap) is contained in the root of the tree. The Heap implemented in this library can either be a Min-Heap or a Max-Heap, and is set on the constructor. For a Max-Heap, the IComparer<T> instance used is wrapped in a ReverseComparer<IComparer<T>> instance, thus reversing the comparison decision and sorting in the opposite order.
[More information on heaps]
Matrix
public class Matrix : IVisitableCollection<double>, IMathematicalMatrix<T>
{
public Matrix Invert();
public bool IsEqual(Matrix m);
public Matrix Minus(Matrix Matrix);
public static Matrix operator +(Matrix m1, Matrix m2);
public static Matrix operator *(Matrix m1, Matrix m2);
public static Matrix operator *(Matrix m1, double number);
public static Matrix operator *(double number, Matrix m2);
public static Matrix operator -(Matrix m1, Matrix m2);
public Matrix Plus(Matrix Matrix);
public Matrix Times(Matrix Matrix);
public Matrix Times(double number);
public Matrix Transpose();
public void AddColumn();
public void AddColumn(params double[] values);
public void AddColumns(int columnCount);
public void AddRow();
public void AddRow(params double[] values);
public void AddRows(int rowCount);
public Matrix GetSubMatrix(int rowStart, int columnStart,
int rowCount, int columnCount);
public void InterchangeColumns(int firstColumn, int secondColumn);
public void InterchangeRows(int firstRow, int secondRow);
public int Columns { get; }
public bool IsSymmetric { get; }
public double this[int i, int j] { get; set; }
public int Rows { get; }
}
The Matrix class corresponds to the Linear Algebra notation of a Matrix. It implements simple operations like Plus, Times, Minus, and IsSymmetric.
The underlying representation of the Matrix class is a simple two-dimensional array of type double.
[More information on matrices]
ObjectMatrix
public class ObjectMatrix<T> : IMatrix<T>, IVisitableCollection<T>
{
public void Accept(IVisitor<T> visitor);
public void AddColumn();
public void AddColumn(params T[] values);
public void AddColumns(int columnCount);
public void AddRow();
public void AddRow(params T[] values);
public void AddRows(int rowCount);
public T[] GetColumn(int columnIndex);
public IEnumerator<T> GetEnumerator();
public T[] GetRow(int rowIndex);
public ObjectMatrix<T> GetSubMatrix(int rowStart,
int columnStart, int rowCount, int columnCount);
public void InterchangeColumns(int firstColumn, int secondColumn);
public void InterchangeRows(int firstRow, int secondRow);
public void Resize(int newNumberOfRows, int newNumberOfColumns);
public int Columns { get; }
public int Count { get; }
public bool IsSquare { get; }
public T this[int i, int j] { get; set; }
public int Rows { get; }
}
The ObjectMatrix class is a simple representation of a 2-dimensional array of objects. It provides some other functionality than a standard jagged array, like resizing the matrix, getting rows and columsn individually, and interchanging rows / columns.
PascalSet
public class PascalSet : IVisitableCollection<int>, ISet
{
public PascalSet Difference(PascalSet set);
public PascalSet Intersection(PascalSet set);
public PascalSet Inverse();
public bool IsEqual(PascalSet set);
public bool IsProperSubsetOf(PascalSet set);
public bool IsProperSupersetOf(PascalSet set);
public bool IsSubsetOf(PascalSet set);
public bool IsSupersetOf(PascalSet set);
public static PascalSet operator +(PascalSet s1, PascalSet s2);
public static bool operator >(PascalSet s1, PascalSet s2);
public static bool operator >=(PascalSet s1, PascalSet s2);
public static bool operator <(PascalSet s1, PascalSet s2);
public static bool operator <=(PascalSet s1, PascalSet s2);
public static PascalSet op_LogicalNot(PascalSet set);
public static PascalSet operator *(PascalSet s1, PascalSet s2);
public static PascalSet operator -(PascalSet s1, PascalSet s2);
public PascalSet Union(PascalSet set);
public bool this[int i] { get; }
public int LowerBound { get; }
public int UpperBound { get; }
}
A PascalSet (so called because it implements a set not unlike the Set class used in Pascal) corresponds to the mathematical notation of a set, where items in some finite universe can be contained in the collection. The PascalSet class implements simple operations like checking subsets, supersets, unions, and differences between sets.
[More information on sets]
PriorityQueue
public class PriorityQueue<T> : IVisitableCollection<T>, IQueue<T>
{
public void Add(T item, int priority);
public void DecreaseItemPriority(int by);
public T Dequeue();
public void Enqueue(T item);
public void Enqueue(T item, int priority);
public T Dequeue();
public IEnumerator<Association<int, T>> GetKeyEnumerator();
public void IncreaseItemPriority(int by);
public T Peek();
}
A Priority queue is a special type of queue where the item dequeued will always be the smallest (in a Min Priority Queue) or the largest (in a Max Priority Queue) of the items contained in the queue. The underlying representation is implemented using a Min/Max-Heap (depending on the type of Priority queue). The maximum/minimum item in a Heap is always kept in the root, and thus at the front of the queue.
Also available are methods to increase priorities and decrease priorities by specific amounts - this doesn't affect the ordering of the items, since all items are affected by the operation.
[More information on priority queues]
ReadOnlyPropertyCollection
public sealed class ReadOnlyPropertyList<T, TProperty> :
IList<TProperty>, IVisitableCollection<TProperty>
{
public ReadOnlyPropertyList(IList<T> list, PropertyDescriptor property);
public void Accept(IVisitor<TProperty> visitor);
public int CompareTo(object obj);
public bool Contains(TProperty item);
public void CopyTo(TProperty[] array, int arrayIndex);
public IEnumerator<TProperty> GetEnumerator();
public int IndexOf(TProperty item);
public TProperty this[int index] { get; }
TProperty IList<TProperty>.this[int index] { get; set; }
}
The ReadOnlyPropertyCollection class is a simple utility collection implementing IList<TProperty>. It exposes a property of a type in a list as another list. For example, List<Person> can be exposed as a List<string> (list of names) through the ReadOnlyPropertyCollection, by using the original list, and not making a copy of that list.
Red Black Tree
public class RedBlackTree<TKey, TValue> : IVisitableDictionary<TKey, TValue>
{
public void Accept(IVisitor<KeyValuePair<TKey, TValue>> visitor);
public void Add(KeyValuePair<TKey, TValue> item);
public void Add(TKey key, TValue value);
public bool Contains(KeyValuePair<TKey, TValue> item);
public bool ContainsKey(TKey key);
public void DepthFirstTraversal(
OrderedVisitor<KeyValuePair<TKey, TValue>> visitor);
public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator();
public bool Remove(TKey key);
public bool TryGetValue(TKey key, out TValue value);
public IComparer<TKey> Comparer { get; }
public TValue this[TKey key] { get; set; }
public ICollection<TKey> Keys { get; }
public TKey Max { get; }
public TKey Min { get; }
public ICollection<TValue> Values { get; }
}
The Red Black Tree is a self-balancing binary search tree. What this means, essentially, is that the the length of paths from the root node to child nodes are controlled - so you can't get an extremely long path to one node, and short paths to the others (which degrades search performance).
The Red Black Tree implemented in NGenerics implements the IDictionary<TKey, TValue> interface.
The insertion and removal algorithms were adapted from Julienne Walker's (Eternally confuzzled) algorithms - if you want to learn about Red Black Trees, look there first.
[More information on Red Black trees]
SortedList
public class SortedList<T> : IVisitableCollection<T>, IList<T>
{
public override void Accept(IVisitor<T> visitor);
public override void Add(T item);
public override void Clear();
public override int CompareTo(object obj);
public override bool Contains(T item);
public override void CopyTo(T[] array, int arrayIndex);
public override IEnumerator<T> GetEnumerator();
public override bool Remove(T item);
public void RemoveAt(int index);
public IComparer<T> Comparer { get; }
public T this[int i] { get; }
}
The SortedList<T> class performs the same function as the default SortedList<TKey, TValue> class in the .NET framework, except that it removes two nuances I've found working with that class:
- Duplicate items can occur in this
SortedList (they're not allowed in the standard one). - Items are sorted by themselves, and no key is needed (the standard
SortedList requires key-value pairs).
SkipList
public class SkipList<TKey, TValue> : IVisitableDictionary<TKey, TValue>
{
public void Accept(IVisitor<KeyValuePair<TKey, TValue>> visitor);
public void Add(KeyValuePair<TKey, TValue> item);
public void Add(TKey key, TValue value);
public bool ContainsKey(TKey key);
public void CopyTo(KeyValuePair<TKey,
TValue>[] array, int arrayIndex);
public IEnumerator<KeyValuePair<TKey,
TValue>> GetEnumerator();
public bool Remove(TKey key);
public bool TryGetValue(TKey key, out TValue value);
public IComparer<TKey> Comparer { get; }
public int CurrentListLevel { get; }
public TValue this[TKey key] { get; set; }
public ICollection<TKey> Keys { get; }
public int MaxListLevel { get; }
public double Probability { get; }
public ICollection<TValue> Values { get; }
}
A SkipList is an ingenious data structure, first proposed by William Pugh in 1990. You can find his original paper here. The crux of a SkipList is that items get duplicated on different levels of linked lists, the level (almost) randomly selected. It allows for quick searching for an item by "skipping" over several list items as opposed to a normal linked list where comparisons would be sequential.
Skip lists are usually implemented in one of two ways, using either several linked lists, or a matrix structure (like a 2D linked list). The SkipList implemented here is implemented using the matrix style, and is based on the excellent work done by Leslie Stanford and ger. It implements the IDictionary<TKey, TValue> interface, and thus can be used like the standard Dictionary<TKey, TValue> class in the framework.
Just note that while the performance is excellent, the duplication of items can cause that you run out of memory very quickly, especially if the maximum number of levels is high.
[More information on Skip Lists]
Default data structures extended
Included in the library are versions of some of the default .NET generic data structures, extended to implement the IVisitableCollection<T> interface. They are :
VisitableHashtable<Tkey, TValue> VisitableLinkedList<T> VisitableList<T> VisitableQueue<T> VisitableStack<T>
Patterns implemented
Singleton
public sealed class Singleton<T> where T: new()
{
private Singleton();
public static T Instance { get; }
private static T instance;
}
A singleton is a pattern used to minimize the instances of a class to one. With the advent of generics in C# 2.0, implementing a generic singleton is very elegant indeed. Another (more or less the same) implementation of the singleton pattern can be found in this article, but I like the value initializing statically more.
Visitor Pattern
public interface IVisitor<T>
{
void Visit(T obj);
bool HasCompleted { get; }
}
The visitor pattern is implemented by all collections inheriting from the IVisitableCollection<T> interface. Visitors inheriting from IVisitor<T> can be used to visit all kinds of collections, being indifferent from the internal structure of the data structure visiting. It provides two methods:
- Visit performs some action on an object. For a simple example, think of a counting visitor applied to a data structure of integers and doing a += operation in the
Visit method. - The
HasCompleted property indicates whether the Visitor wants to continue visiting the rest of the objects contained in the collection. This is useful for searching visitors for example, where it can stop visiting when it has found the object it's looking for.
[More information on the Visitor Pattern]
Sorters
The ISorter interface
public interface ISorter<T>
{
void Sort(IList<T> list);
void Sort(IList<T> list, SortOrder order);
void Sort(IList<T> list, IComparer<T> comparer);
void Sort(IList<T> list, Comparison<T> comparison);
}
Multiple sorters are implemented in this library. The default .NET framework libraries don't give us much choice in terms of sorting, and thus these were born. It's generic in the sense that any class implementing IList<T> can be sorted, as long as the contained items either implement the IComparable<T> interface or a IComparer<T> instance is provided.
The following sorters are provided:
Algorithms
Dijkstra's Algorithm
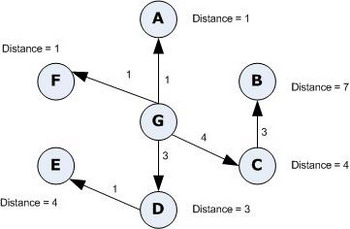
Dijkstra's algorithm provides a solution for the shortest paths, single source problem in graphs. In other words, given a directed or undirected Graph<T> as input, the outputs is a graph representing the shortest path from the source vertex to every other vertex in the graph (if the vertices are reachable from the source vertex). As an example, see the input and output graphs with the source vertex G, below.
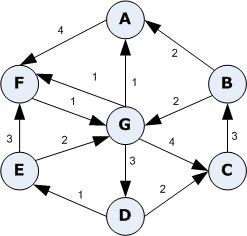
| | 
|
| Input Graph | | Output Graph - Shortest Paths |
[More information on Dijkstra's Algorithm]
Points of interest
The lack of support for covariance in C# makes it appealing to avoid interfaces for this type of work, simply because using them would end up forcing the programmer to cast much more than needed (or the developer of this library to do a bucket load of implicit implementations).
Also, coming from a C++ background, support for multiple inheritance and private / protected inheritance would have changed this design a lot. Hopefully, we'll see support for this one day in some distant version of the language specification.
So, what's next?
- Some sorters still to come (Radix sort, Library sort, Smooth sort, Introsort, Patience sort, ...).
- Graph algorithms (spanning trees, critical path analysis, etc.).
- An implementation of a Red & Black Tree.
- A Fibonacci Tree.
- Many more that's not on my short list. This might be a never-ending project, but I will make a concerted effort to add only useful stuff.
References
- C# Sorters [Link]
- Bruno R. Preis - Data Structures and Algorithms with Object-Oriented Design Patterns in C# [Link].
- All other links contained in this article (Wikipedia, etc.).
History
05 March 2007: 1.2
Added stuff:
ObjectMatrix HashList RedBlackTree ReadOnlyPropertyCollection
Changed stuff:
- Graph's
AddVertex(T item) and AddEdge(Vertex<T> v1, Vertex<T> v2) now return the newly created vertex and edge, respectively. - Extracted interfaces
IMathematicalMatrix and IMatrix for Matrix type structures. - Added
ToKeyValuePair() method on Association class. - Converted the
BinarySearchTree<T> to BinarySearchTree<TKey, TValue>: it now implements the IVisitableDictionary<TKey, TValue> interface. VisitableList<T> and GeneralTree<T> now implements ISortable<T> and ISortable<GeneralTree<T>>, respectively. - Methods added to the
ISorter<T> and ISortable<T> interfaces to allow sorting with a Comparison<T> delegate. InterchangeRows, InterchangeColumns, GetRow, GetColumn, AddColumn, AddRow added on IMAtrix, Matrix, and ObjectMatrix. - Added
Parent property to GeneralTree<T> so bottom-up paths can be found. - Added
Ancestors property to GeneralTree<T> to find any ancestors of the current node up in the tree.
28 December 2006: 1.1 (NGenerics)
In an effort to take this project one step further, DataStructures.NET has received a bit of a face-lift, and is now dubbed NGenerics. The project page can be found here. The latest source can be found on the project page, but it will be periodically updated at CodeProject.
As such, major changes have been made:
- The default namespace has been changed to
NGenerics. - The strong name key for signing the assembly has been changed and is no longer distributed with the library. This means that if you want to compile NGenerics from source, you need to provide your own key (or turn off signing for the assembly).
- Hopefully, this will be the last major change - things should settle down now...
Added stuff:
BinarySearchTree - Euclid's Algorithm
Changed stuff:
- Added
FindNode method to BinaryTree, GeneralTree, and the ITree<t> interface. - Changed the
IsSymmetric method of Matrix to not make a transposition of the current matrix. - Extracted interface for
Matrix: IMatrix. - Added methods/properties to
Matrix: IsSquare, GetSubMatrix, and Clone (Matrix now implements IClonable) .
A detailed history can be found with the source.
