Binary Tree Introduction

• Download demo project - 8 KB
• Download source - 2.6 KB

Introduction

In this article, I have given an introduction of binary trees and hierarchical data structures. In the sample project, I have compared binary trees with qsort. The binary tree is defined with a C++ template. It can be used from any environment supporting C++, and for any data type supporting data comparison operators, < and >. The description is easy to follow. To use the template, you need to include BTree.h in your C++ project. For balancing and optimization of data insertion, I have used a simple reordering method instead of Red-Black and AVL trees. The advantage is that data insertion and tree-creation require slightly less time. Even if not perfectly balanced, this method ensures that the data search requires <code>log2 comparing operations.

My major interests are multi-dimensional data structures so I mostly utilize algorithms which can be easily generalized for N-dimensions.

Background

Binary trees are hierarchical data structures which allow insertion and a fast, nearest-neighbours search in one-dimensional data. It can be used instead of qsort and binary search to quickly find the closest points in a data array. The binary tree has the advantage of having a simple structure that allows generalization for more than one dimension - the so-called KD Tree. Therefore, it is good to understand how it works and how it performs data searches. I will keep the explanation clear and easy to follow.

First let's define a tree. A tree is a data-structure composed from a set of nodes. Each node has links to a number of other nodes called children and parents. The difference between them is that children are chosen by some criterion while the parent links merely keep the history of how we have reached a given node.

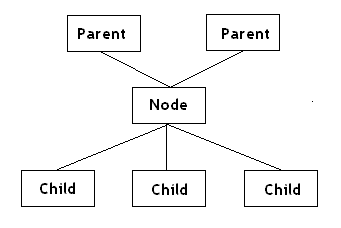
The binary tree has two children - <code>Left and <code>Right and one parent. The parent link is necessary for nearest-neighbours searching and for optimization of the tree.

Each node of the tree contains some type of data with value X. The left child node must have a smaller X value than the corresponding right value - <code>X > Left->X and <code>Right->X > X. This is the basic criterion of the binary tree. The tree also has a <code>Root. The root is the only node which does not have a Parent. When a new node with value X needs to be added to the tree, we always start from Root and go down in the tree until we reach an empty location. Each time when we pass through a node, we decide to go left or right by comparing the value X with the values of the node - if X is smaller, we go left, if it is bigger, we go right.

In the above example, the new value is 100. To find the location of this value, follow the steps within the tree. Starting from the root we check if 100 is smaller or bigger then 127. In this case it is smaller so we go left in the node with value 111. Now, 100 is smaller than 111 so we go left to node 60. This time 100 is bigger, but 60 does not have a Right child, it is an empty location, so we attach 100 here.

Now let's see how the binary tree can be used for something useful. Let's see how the limiting range and the nearest neighbour can be found. Let us choose a new value, 125, for example. Between the two existing tree values, we need to determine which is 125. Again, we start searching the Parent node of 125 and after few steps, we reach node 115:

It is clear now that since 125 is the Right child of 115, 125 is the closest from the leftmost neighbour. But the search for the right value is not so simple. In this case, the Root of the tree is 127. The rule for binary trees is that the limiting value is the first Parent node with a value bigger than 125. So we have to go up in the tree until we find a Parent with a value bigger than 125. It is possible in some cases that the node has only one limiting neighbour. The code for binary tree declaration, data insertion and nearest neighbour search is given below.

Code

The declaration and implementation of binary tree is in BTree.h. The class BTNode contains insert and remove functions. The template type is X, with two pointers to the left and right children, and one to the parent. I have made only two small extensions over the standard binary tree, and added one member property - ParentOrientation defined as bool, and one member function - moveup() used to optimize insertion.

//Binary Tree Node
template <class>
class BTNode
{
public:
    BTNode();
    BTNode(Xtype x);
    bool Delete_Tree(BTNode<xtype>* Root);
    BTNode(BTNode<xtype>* k1, BTNode<xtype>* k2);
    BTNode<xtype> *Left, *Right, *Parent;
    BTNode<xtype>* place(BTNode<xtype>* T);
    BTNode<xtype>* insert(Xtype x,bool&root_changed,bool optimize=true);
    bool insert(BTNode<xtype>* node,bool&root_changed,bool optimize=true);
    void remove();
    int count_childs();
    bool  moveup();
    Xtype x;
    bool ParentOrientation ; //where is child WRT parent ? 0=left 1=right
};

The ParentOrientation member is used for optimization of insertion and nearest-neighbour search. It identifies what the orientation of a child is with respect to its parent; if it is 0, the child is from the left of the parent, if it is 1 it is on the right. Of course, we can determine this just by comparing the values of the child and the parent, but since the comparing operators < and > can be slow, I have used this flag to decrease their use. The member function moveup() tries to move the node up in the tree. It improves the balance of the tree and optimizes the insert operation. The Insert then looks like this:

//insert node to the tree, starts from current node
template <class>
bool
BTNode<xtype>::insert(BTNode<xtype>* node,bool&root_changed, bool optimize)
{
    BTNode<xtype>* pNext = this;
    BTNode<xtype>* pFather;
    while(pNext) //do not insert if already exist
    {
        pFather = pNext;
        if(node->x < pNext->x)
            pNext = pNext->Left;
        else if(node->x > pNext->x)
            pNext = pNext->Right;
        else 
            return false;
    }

    if(!pNext) //empty place, do not insert value twice
    {
        node->Parent = pFather;
        if(node->x < pFather->x)
        {
            pFather->Left = node;
            node->ParentOrientation = 0 ;
        }
        else
        {
            pFather->Right = node;
            node->ParentOrientation = 1;
        }

        if(optimize)
            root_changed = node->moveup();
        else 
            root_changed = false ;

        return true;
    }
    return false;
}

Nearest-neighbour search is explained in the previous section. Below is the code:

/*   nearest neighbours search
   input:
    Root - the root of the tree
    x - template type with search target value

   output:
    l - the left limiting value or INVALID_VALUE if there 
is no neighbour to left
    r - the right limiting value or INVALID_VALUE if there 
is no neighbour to right
    
   returns:  
      - the closest value to x
      - INVALID_VALUE - empty tree 
*/
template <class>
Xtype FindNearest(BTNode<xtype>* Root, Xtype x, Xtype* l, Xtype* r)
{
    Xtype left,right;
    BTNode<xtype>* pNext = Root;
    BTNode<xtype>* pFather;
    bool ParentOrientation ;
    while(pNext)
    {
        pFather = pNext;
        if(x<pnext->x)
        {
            pNext = pNext->Left;
            ParentOrientation = false; 
        }
        else if(x>pNext->x)
        {
            pNext = pNext->Right;
            ParentOrientation = true; 
        }
        else 
        {
            *l = pNext->x;
            *r = pNext->x;
            return pNext->x;
        }
    }

    if(!ParentOrientation)  //x < pFather->x
    {
        right = pFather->x;
        //go up in the tree    and search for the left limit
        ParentOrientation = pFather->ParentOrientation ;
        pFather = pFather->Parent;
        while(pFather && !ParentOrientation)
    { 
           //search parent to the left
            ParentOrientation = pFather->ParentOrientation ;
            pFather = pFather->Parent;
        }

        if(!pFather)
        {
            *l = INVALID_VALUE;  //no neighbour to the left
            *r = right;
            return right;
        }
        else
        {
            *l = pFather->x;
            *r = right;
            return (x-pFather->x < right-x ? pFather->x:right);
        }
    }

    else //x > pFather->x
    {
        left = pFather->x;
        // go up in the tree and search for the right limit        
        ParentOrientation = pFather->ParentOrientation ;
        pFather = pFather->Parent;
        while(pFather && ParentOrientation)
    { 
           //search parent to the right
            ParentOrientation = pFather->ParentOrientation ;
            pFather = pFather->Parent;
        }

        if(!pFather)
        {
            *l = left;  
            *r = INVALID_VALUE;   //no neighbour to the right
            return left;
        }
        else
        {
            *l = left;
            *r = pFather->x;
            return (x-left < pFather->x-x ? left:pFather->x);;
        }
    }

    return INVALID_VALUE; //empty tree 
}

As was mentioned above, optimization of the tree is realized with moveup() routine. Why is optimization needed? Well, if the values contained in the tree come in random (not ordered) sequence, the tree will be naturally balanced. However, there is no guarantee that values are not going to come in some non-random pattern. For example, if it is something like 2,5,8,11..., then the binary tree will become a linked list and the search of nearest neighbours will become sequential search, which is ineffective. There are a lot of balancing methods - Red-Black,AVL... I prefer my own local tree optimization which removes the worst cases. The illustration below shows how it works:

Here N is the node to be inserted, P is its parent, and G is its grand-parent. If it happens like in both cases shown above on the left, or it mirror cases, it is possible to move P or N up, and G down in the tree. The three nodes - N, P and G are reordered as shown on the right. In this way, the height of the tree is decreased, the worst cases are corrected and the balance of the tree is improved. From the test I performed, I discovered that the insert operation and tree creation are less than 10% slower. If you increase the average height of randomly chosen data, you find that performance is still 10% slower, but this percentage rises with data size and ensures that the average height is always log₂N, where N is the data size. This means that the average path which we will pass while looking for a value in a large array (100 000)will be about 20, because 2 of power 20 makes 100 000. The project source contains the application performing these tests. If you want to check the average tree height for different points, change the numbers for POINTS_NUM and change the generate_random_point() routine if it is too big.

License

This article has no explicit license attached to it, but may contain usage terms in the article text or the download files themselves. If in doubt, please contact the author via the discussion board below.

A list of licenses authors might use can be found here.