Old versions:
Running Example:
Exported Image:

Introduction
Graphical User Interfaces can provide many alternatives of understanding for a same concept, and, a Tree is one of the basic data structures learnt in Computer Science courses.
Tree Diagrams, Tree Charts, or Tree Shaped Drawings, provide a quick and easy understanding of hierarchical structures, search maps, evolution and inheritance, phrase structures, organizational charts, or mind maps, and, from there, a wide range of applications.
This is a basic description of a drawing algorithm, just an explanation from a personal approach of a layout. I hope it could help or serve as a basis for some future project, some extended function, or just as a simple ‘help’.
Perhaps it has been, there are others, and there will be further explanations, other methods, different ideas to achieve the same target, but, the way we understand is not the same for all of us, there is no universal law, or universal way of descriptions that is understandable for all the world, so, this is a contribution, for some group of people, that could take advantage of it, or expand it for the commonweal.
Background
In the middle of my major, when I was taking a subject on Automata Theory Languages, we were asked to develop a program whose main task was to validate “context free grammars”, and as a second purpose, it would be nice to have drawn the “parser tree”.
In those years, Java version was 1.4 and my team chose it for programming the homework, and, since the drawing was not the main part of the project (theoretical logic was), we left that until last, and our drawing was not very aesthetic...
In the same semester, my friend Tomás Ortíz S. was smarter, he used a tree component from VB… the task requested from our teacher was fulfilled, and the nodes were drawn in order and grouped properly. So, in other words, he was efficient and saved time.
Years later I graduated, that project came to my mind, and I remembered how we wondered (at that time) why there didn’t exist a component to draw tree shapes or graphs… Recently, I’ve made some searches for it, and I didn’t found many projects on it (at least someone where the method was described). I know trees are simple, but, taking in count that, I left my mind grouping a lot of uses for this structure, which I mentioned in the introduction. Of course, we have now several diagram tools… but in my particular point of view, we jumped from the original need to the final applications without documentation in the process. This article intends to fill that gap.
I must say… I wrote the last paragraph to identify my first and main motivation to write this article, but then I have to admit, that trying to reassure myself that there is not so much information, I was mistaken, what I originally considered 4 or 5 options… turned to be more than 10 different approaches, which I would like to summarize and list as links at the end in the References section. I didn’t consider all of them at the beginning, but after I tried different search terms “tree viewer”, “tree drawing code”, “tree painter”, “graph”, “visualization”… I found a lot of “branches” of derivations. I hope to maintain that list and keep it growing with the community suggestions.
Using the Code
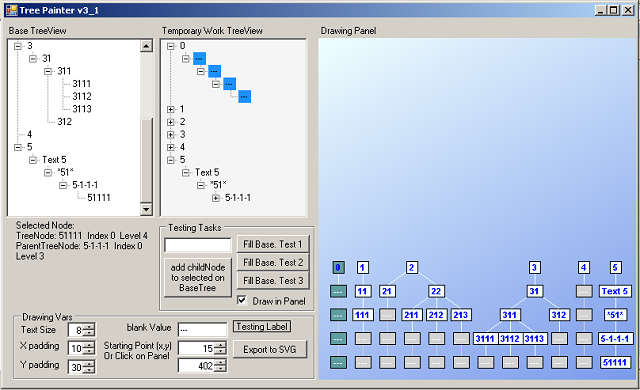
Two components are taken as a basis: TreeView and Panel. Both became standard, they are well documented, and vastly exemplified. The exposed code evolved in 3 “main” versions, and in the third one, the Label control was added to identify each node.
For beginners and intermediates, this article will maintain its ‘first approach’ objective. Making a User Control or Component, or Exposing the code as WebService could be a second release of this task.
For Input, I decided to use the TreeView. For Output, I could take a Canvas if I only wanted to draw Rectangles or Ellipses… but after a small analysis, you can realize that a Panel offers the Canvas Graphics object and serves as a Container for our ‘nodes’ (Labels in version 3).
In this article, I will address mainly the last version of the source code. Comments are located in the code and the same principle is applied from the first version.
Analysis
Let’s start. Let’s say that we have some Trees with different amount of nodes:


Images 1, 2 and 3 are simple examples. And in each example, complexity increases. These are ‘hand-made’ layouts.
And the main question is: How to locate each node in a ‘nice’ way? Well… this is a key point… it should be a task to dedicate several hours. If you continue reading… you will private yourself of solving this puzzle and perhaps some develop in your mind. But also, you can start from this article and develop a new alternative.
Having said that… Let’s assume we calculate the last level for each branch…
For the first tree images, the level is the same for all the ‘children’…
For images 4, 5 and 6, there is a different ‘depth’ on each branch.
The key point (to have a arrangement of nodes) is to “balance” (in the absence of a better word) the tree. In other words, fill each branch, so each one contains the same amount of levels (depth). It is not necessary to have the same amount of children on each branch, we only need the same amount of levels. Image 5 can give you an approximation of how to imagine “the missing” nodes in the shorter branches (How will you balance that tree?). After you start to analyze, the same principle could be applied for any kind of branch or tree. Just “fill in the blanks”. Image 5 shows by coincidence the same amount of children below each branch, Image 6 shows that it’s not necessary to have the same amount of children. Images 5 and 6 show missing nodes in gray colors.

Now, this is the full layout, and the next question could be, from where to start drawing?. How do we know the centered location for each “father node”? This is another good question (when you know nothing at all).
Suppose that we mix image 3 and 4.

We could have a “first nice layout”:

But if we append the imaginary missing nodes, then those could be “overlayed”…

After watching the layout of images 5 and 6… if we look for the smallest spaces or “continuous nodes”, it’s easy to find that the deepest level can determine the first location of a node without expanding above levels.
Starting with a simple example, the sequence will be the following:

So, another key point would be to start from the bottom (the deepest level) and then determine the location of the father. I’m assuming that a good tree or node structure (different or alternatives to the TreeView) should determine easily the father of a node.
The code explained below will make use of the analysis previously exposed. Check the comments.
Code
The main functions are pasted here, but I would suggest to check the code in the source code and debug it.
I would say that <code>locateNodes is the main function which implements the algorithm explained in the Analysis.
private int getAllChildNodes(TreeNodeCollection nodes, ArrayList array)
...
private void addBlankNode(TreeNode t, int untilLevel)
...
private void locateNodes(Panel drawingPanel, TreeView originalTree,
TreeView tempTree, out ArrayList labeledNodes)
{
tempTree.Nodes.Clear();
Label labelAux;
labeledNodes = new ArrayList();
if (originalTree.Nodes.Count == 0)
return;
#region drawing variables
Graphics board = drawingPanel.CreateGraphics();
int x = 20;
int y = 20;
int maxDepht = 0;
ArrayList list;
ArrayList[] listByLevel;
int xInitial = int.Parse(xStart.Value.ToString());
int yInitial = int.Parse(yStart.Value.ToString());
this.drawNodeFont = new Font("Arial",
float.Parse(fontSize.Value.ToString()),FontStyle.Bold);
#endregion
list = new ArrayList();
int totalNodes = getAllChildNodes(originalTree.Nodes, list);
foreach (TreeNode n in list)
if (n.Level > maxDepht)
maxDepht = n.Level;
listByLevel = new ArrayList[maxDepht + 1];
foreach (TreeNode n in list)
if (n.Level == 0)
tempTree.Nodes.Add((TreeNode)n.Clone());
list = new ArrayList();
totalNodes = getAllChildNodes(tempTree.Nodes, list);
foreach (TreeNode n in list)
if (n.Nodes.Count == 0 && n.Level < maxDepht)
addBlankNode(n, maxDepht);
list = new ArrayList();
totalNodes = getAllChildNodes(tempTree.Nodes, list);
foreach (TreeNode n in list)
{
if (listByLevel[n.Level] == null)
listByLevel[n.Level] = new ArrayList();
listByLevel[n.Level].Add(n);
}
x = xInitial;
y = yInitial;
for (int z = maxDepht; z >= 0; z--)
{
for (int index = 0; index < listByLevel[z].Count; index++)
{
TreeNode nodeToPaint = (TreeNode)(listByLevel[z][index]);
labelAux = new Label();
labelAux.Name = nodeToPaint.Name;
labelAux.Font = drawNodeFont;
labelAux.Text = nodeToPaint.Text;
labelAux.TextAlign = System.Drawing.ContentAlignment.MiddleCenter;
labelAux.AutoSize = true;
labelAux.BorderStyle = BorderStyle.FixedSingle;
labelAux.MouseLeave += new System.EventHandler(this.lblTest_MouseLeave);
labelAux.MouseEnter += new System.EventHandler(this.lblTest_MouseEnter);
labelAux.Tag = nodeToPaint;
if (nodeToPaint.Text == txbBlankValue.Text)
{
labelAux.BackColor = this.disabledNodeBackColor;
labelAux.ForeColor = this.disabledNodeForeColor;
}
else
{
labelAux.BackColor = this.enabledNodeBackColor;
labelAux.ForeColor = this.enabledNodeForeColor;
}
unionNodeLinesPen = new Pen(labelAux.BackColor);
labelAux.Location = new Point(x, y);
nodeToPaint.Tag = new Rectangle(labelAux.Left,
labelAux.Top,
labelAux.PreferredWidth,
labelAux.PreferredHeight);
if (z < maxDepht)
{
Point posFirstChild =
getRectangleCenter((Rectangle)(nodeToPaint.FirstNode.Tag));
Point posLastChild =
getRectangleCenter((Rectangle)(nodeToPaint.LastNode.Tag));
Point relocatedPoint = labelAux.Location;
relocatedPoint.X = (posFirstChild.X + posLastChild.X) / 2 -
labelAux.PreferredWidth / 2;
System.Console.WriteLine(nodeToPaint.Text + " x= " + relocatedPoint.X
+ "\n ->1: " + nodeToPaint.FirstNode.Text + " (" + posFirstChild.X + ");"
+ "\n ->2: " + nodeToPaint.LastNode.Text + " (" + posLastChild.X + ");");
labelAux.Location = relocatedPoint;
nodeToPaint.Tag = new Rectangle(labelAux.Left,
labelAux.Top,
labelAux.PreferredWidth,
labelAux.PreferredHeight);
}
foreach (TreeNode t in nodeToPaint.Nodes)
{
Rectangle r = new Rectangle(labelAux.Left,
labelAux.Top,
labelAux.PreferredWidth,
labelAux.PreferredHeight);
Point parentCenterPos = getRectangleCenter(r);
Point childCenterPos = getRectangleCenter((Rectangle)t.Tag);
childCenterPos.Y = ((Rectangle)t.Tag).Top;
board.DrawLine(unionNodeLinesPen, parentCenterPos, childCenterPos);
}
labeledNodes.Add(labelAux);
x = labelAux.Left + labelAux.PreferredWidth +
int.Parse(xPadding.Value.ToString());
System.Console.WriteLine("Calculated X:" + x.ToString());
}
y -= int.Parse(yPadding.Value.ToString());
}
(Point)((TreeNode)(listByLevel[0][listByLevel[0].Count - 1])).LastNode.Tag;
}
Points of Interest
At the beginning, I decided to find a solution for this problem as a personal challenge, but after I saw my comments on the code, I wondered if this could be considered as my first contribution to the open source, and after some days, I decided to make the first step to publish and perhaps receive a learning feedback from the community, I think I have nothing to lose (and that’s the spirit of CodeProject).
I decided to check if someone else has solved this before, and it was a nice learning how different needs could make use of the same principle. It was also very interesting to summarize the different projects that called my attention. Deployments in C#, Java, Python, WPF, and also the currently experimental feature of Google Charts (I think these guys now they have a lot from where to choose).
My puzzle and personal challenge became a research of other solutions, and also a learning of different online tools, theory, and notation. I originally imagined “a handful” or “a lot” of applications, but in fact, there’s “a huge” range if you consider all the alternatives.
Search for:
History
A brief summary of the versions:
- V1. One form. A tree view. A panel. Nodes of limited size are drawn on the
OnPaint event of the Panel component. Text is drawn but margins between nodes are not calculated, text length is not calculated either. - V2. Reorganized Tester GUI.
Nodes are of dynamic size. Internal Rectangles specify the Location (as “x,y” coordinates), and boundaries (width and height of the text).
Text Width is calculated based on Font object.
Font Size is dynamic.
A dynamic ‘starting point’ is added. (Starting point means the bottom left position where the first and deepest child is located).
Horizontal and Vertical Margins are dynamic.
Bug. Panel does not show those nodes which are out of the visible area. - V3. Labels are added. Internal Rectangles are eliminated.
Size does not require to be calculated since Label.Autosize property does the work.
Panel shows all the nodes, those 'out' of visible area are shown through scrollbars. - V3.1 Export to SVG file option is enabled (internal and basic SVG format generation, no particular library is used).
Future
Expose as WebService:
Ideas/Proposals:
Propose a circular (radial) layout:
If we have two first level nodes, those will be separated 180°.
If we have three first level nodes, those will be separated 120°.
Thus... 360° / nodes is the formula to arrange them symmetrical, but when the amount of branches increases, the position of the deepest levels should be considered in order to not overlay...
This being my first post on CodeProject, wise comments will be appreciated, as well as any suggestions will be treated with respect and consideration.
