Art Gallery Problem: polygon triangulation & 3-coloring

• Download demo project - 257.3 KB
• Download source files - 313.1 KB

Introduction

From Wikipedia

The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. The motivation for the problem is the real-world problem of guarding an art gallery with the minimum number of security cameras that can each rotate to obtain a full field of vision. In the computational geometry version of the problem the layout of the art gallery is represented by a simple polygon and each security camera is represented by a point in the polygon. A set S of points is said to guard a polygon if, for every point p in the polygon, there is some such that the line segment between p and q does not leave the polygon.

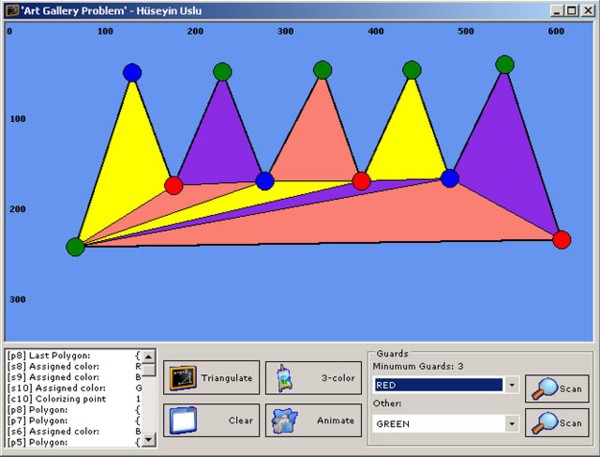
As in my computational-graphics course, I was requested to implement a solution program to the art gallery problem stated above. So using cut-ear triangulation and 3-coloring algorithms, I did implement the above program in screenshot.

Background

The reader needs to have basic knowledge of computational-geometry (polygons, points, etc..)

Theory

Two-Ears

A principal vertex pi of a simple polygon P is called a ear if the diagonal (pi-1, pi+1) that bridges pi lies entirely in P. We say that two ears pi and pj are non-overlapping if the interior of triangle (pi-1, pi, pi+1) does not intersect the interior of triangle (pj-1, pj, pj+1)

Note: The program code uses 'Polygon Triangulation in C#' of fgshen (http://www.codeproject.com/csharp/cspolygontriangulation.asp) as skeleton triangulation code. For more info about the triangulation and two-ears theorem, please check the page.

3-coloring

Graph 3-coloring is the task of coloring each node of the graph either red, green, or blue with the constraint that the two endpoints of any edge must get different colors.

Using the code

Basically the code is developed with Visual Studio 2005 using C#. The code uses the
System.Drawing library for most drawing and computational-geometry.

Here's a class list for the code.

Triangulation - triangulate()*

Handles the two-ears theorem triangulation algorithm.

public void triangulate()   // triangulate the bigger polygon-shape
{
    mPolygon poly = new mPolygon(updated_vertices); 
                    // create a polygon from the current vertices
        Boolean finished = false; // triangulation-finished?

        if (updated_vertices.Length == 3) 
                    // if there's only 3 points, no need to run algorithm
            finished = true;

        Point p = new Point();

        while (finished == false)   
                    // loop while triangulation not finished yet
        {
        int i = 0;
                Boolean not_found = true;   
                        // did we found an ear? no, not yet
                while (not_found && (i < updated_vertices.Length)) 
                        // while we did not found any ear and 
                        // not yet processed all vertices
                {
                    p = updated_vertices[i];    // get current point
                    if (is_ear(p))              
                        // check if we can get an ear from that vertice
                        not_found = false;      // good we found one
                    else
                        i++;                    // continue to search
                }

                update_vertices(p);             
                    // remove the vertice we found the ear 
                    // from the updated_vertices list
                poly = new mPolygon(updated_vertices);  
                    // reupdate the polygon from the rest of vertices
                if (updated_vertices.Length == 3)   
                    // if there's only 3 vertice left
                    finished = true;                
                    // this means we finished the triangulation
    }

    // when the CS:IP reaches here, this means triangulation finished
    polygons = new Point[ears.Count + 1][]; 
                    // init polygons structure to ears.count + 
                    // 1(for last 3 points left)
    for (int i = 0; i < ears.Count; i++)
    {
        Point[] points = (Point[])ears[i];  
                    // move ears to final triangulated polygons list
                polygons[i] = new Point[3];
                polygons[i][0] = points[0];
                polygons[i][1] = points[1];
                polygons[i][2] = points[2];
            }

                // we have 3 left vertices on updated_vertices list, 
                //    - the last triangulated polygon -
            polygons[ears.Count] = new Point[updated_vertices.Length]; 
                // add it to triangulated polygons list also
            for (int i = 0; i < updated_vertices.Length; i++)
            {
                polygons[ears.Count][i] = updated_vertices[i];
            }
}

Triangulation - is_ear()*

Check if given point is in a valid ear.

private Boolean is_ear(Point p) // checks if given vertice is in a ear
{
    mPolygon m = new mPolygon(updated_vertices); 
                    // init. a polygon from the current vertices

    if (m.is_vertex(p) == true) // if given point is a vertex
    {
        if (m.vertex_type(p) == VertexType.ConvexPoint) 
                    // and it's a convex point
                {
                    Point curr_point = p;
                    Point prev_point = m.get_prev_point(p); 
                    // find previous adjacent point
                    Point next_point = m.get_next_point(p); 
                    // find next adjacent point

                    for (int i = updated_vertices.GetLowerBound(0); 
                    i < updated_vertices.GetUpperBound(0); i++) 
                            // loop through all other vertices
                    {
                        Point pt = updated_vertices[i];
                        if (!(is_points_equal(pt, curr_point) || 
                          is_points_equal(pt, prev_point) || 
                          is_points_equal(pt, next_point)))
                        {       // if pt is not equal to checked vertice or 
                            // its's next and prev adjacent vertices
                            if (is_point_in_triangle(new Point[] 
                        { prev_point, curr_point, next_point }, pt)) 
                            // check pt lies in triangle
                                return false;   
                            // if another vertice lies in this 
                            // triangle, then this is not an ear
                        }
                    }
                }
                else         // concave
                    return false; 
                            // we cannot make ears from concave points

                return true;    // if CS:IP reaches here, this means 
                            // vertice passed the test and is an ear
    }
    return false;             // if the given vertex is not an vertex, 
                            // it's not related to an ear also!
}

3-Coloring - traverse()

Start point for 3-coloring algorithm. Colors the last processed polygon and calls the deep-first coloring algorithm

public void traverse() // travers the triangulated polygons list for 
            // assigning 3-colors
{
    int last_poly = polygons.Length - 1; // find last polygon on list
    lb.Items.Add("[p" + last_poly + "] Last Polygon: \t" + 
        polygons[last_poly][0] + polygons[last_poly][1] + 
        polygons[last_poly][2]); // debug message

    // directly assign last polygons vertex's colors
    vertex_colors[get_index(polygons[last_poly][0])] = vertex_color.Red;
    vertex_colors[get_index(polygons[last_poly][1])] = vertex_color.Blue;
    vertex_colors[get_index(polygons[last_poly][2])] = vertex_color.Green;

    colorize(0); // start deep-first 3-color algorithm
}  

3-Coloring - colorize()

Deep-first algorithm to assign colors for vertexes.

public void colorize(int i) // algorithm for colorizing points
{
    int next = i + 1;
    if (next < input_vertices.Length) // use deep-first strategy
    {
        colorize(next);
    }
    find_polygons(input_vertices[i]); // find given points related polygons
} 

3-Coloring - find_polygons()

Find polygons related for a given point. Used in 3-coloring algorithm for finding a given points related polygons and if there's non-color assigned vertex in that found polygon, the code assigns it a color.

public void find_polygons(Point p) // find given points related polygons
{
int v0_index, v1_index, v2_index;

    for (int i = polygons.Length - 1; i > -1; i--) 
                    // loop through all polygons
    {
        if ((p == polygons[i][0]) || (p == polygons[i][1]) || 
                 (p == polygons[i][2])) 
                // if given point is one of the vertexes of current polygon
                {
                    for (int j = 0; j < 3; j++) 
                        // check polygons all 3-vertexes colors
                    {           // vertexes are rounded and each one is 
                        // checked with two other
                        v0_index = get_index(polygons[i][j]);   // vertex1
                        v1_index = get_index(polygons[i][(j + 1) % 3]); 
                                                // vertex2
                        v2_index = get_index(polygons[i][(j + 2) % 3]); 
                                                // vertex3

                        if (vertex_colors[v0_index] == vertex_color.Empty) 
                            // if selected vertex's color is not set yet
                        {
                            vertex_colors[v0_index] = 
                            find_color(vertex_colors[v1_index], 
                                vertex_colors[v2_index]); 
                                // try to set a color to it using 
                                // other two vertexes colors
                                lb.Items.Add("[s" + v0_index + "] 
                            Assigned color: \t" + str_color
                            (vertex_colors[v0_index]) + " {" + 
                            str_color(vertex_colors[v1_index]) + 
                            " ," + str_color(vertex_colors[v2_index]) + 
                            "} " + polygons[i][j]); // debug message
                        }
                    }

                }
    }
}

Running the program

Drawing a polygon

Using the left mouse button, mark the vertices of the polygon.
Use the right mouse button to let program finalize the polygon.

Triangulate

Use the Triangulate button to let program run triangulation algorithm.

3-Color

Use the 3-Color button to let program 3-color the vertices.

Animation

The program can animate the 3-coloring algorithm both using the animate button or by clicking a step in listbox.

Guard-Scanning

The program can scan selected guards view area by the scan buttons.

History

• 04.05.2007 - Initial post

References

* Triangulation code mostly based on http://www.codeproject.com/csharp/cspolygontriangulation.asp