Finding non-cyclical paths between arbitrary pairs of nodes

Introduction

This problem I once had to tackle when working on the design and implementation of routing optimization algorithms for telecommunication networks. Given that a wide area network with nodes and interconnecting links can be modeled as a graph with vertices and edges, a frequently occurring problem is to discover all possible path combinations (containing no cycles) between any pair of communicating end nodes. Please note that this is not a problem of just finding the shortest path between a pair of nodes, for which Dijkstra’a algorithm can be readily employed.

An additional factor is that the algorithm should be able to handle both graphs with uni-directional (one-way) edges and graphs whose edges are assumed to be bi-directional.

Source code and similar C++ algorithm implementations are available at the here.

Background

The National Institute of Standards and Technology (NIST) online Dictionary of Algorithms and Data Structures describes this particular problem as “all simple paths” and recommends a depth-first search to find all non-cyclical paths between arbitrary pairs of nodes.

Modeling the Networks

The link connectivity is modeled using the following Link class with which to identify the end nodes of individual links:

class Link
{
public:

    Link( int source, int target ) 
    {        
    sourceNode = source;
    targetNode = target;        
    }
    
    void GetSourceTargetNodes( int& source, int& target )
    {
    source = sourceNode;
    target = targetNode;
    }
    
protected:
    int sourceNode;
    int targetNode;
};

Here is the Network class with which to store the topology information and perform basic operations such as adding new links, checking the existence of links, and setting the bi-directional status of the network:

class Network
{
private:
        
    std::map< std::pair<int,int>, Link*> link_map;        
    bool bi_direction;    

public:

    Network();
    ~Network();

    void Reset();    
    void SetBiDirection( bool bi );            
    void AddLink( Link* l );
    void AddLink( int s, int d );

    bool LinkExists( int sourceID, int targetID );
    bool BiDirectional();

    std::vector< int > GetAdjNodeIDs( int n );                 
};

A standard STL map is used to house all the network links: the key value consisting of a std::pair uniquely identifies each link element, and are mapped to pointers to Link objects:

std::map< std::pair<int,int>, Link*> link_map;

Unlike sequence containers, such as a std::vector, an associative container such as a std::map is particularly efficient at accessing its elements by their key. Perhaps for very large networks, some kind of hash table may result in further improvements in efficiency, but I’ve stuck with the std::map for now.

Link Bi-Direction Status

If the bi-direction status value is set to true, then a link between end nodes [a,b] would be treated the same as if the link’s end nodes were [b,a].

So when adding new links in bi-directional mode, if a link has already been created and added by specifying the end nodes [2,5] then trying to add another link between end nodes [5,2] will be unsuccessful, since it would be deemed to already exist. For directed (uni-directional) graphs, ie the bi-direction status set to false, adding another link between end nodes [5,2] will succeed, as they are regarded as two separate links.

The Depth-First Search Algorithm

As can be seen from the code sample, beginning from the start node, the algorithm examines all outgoing links and progresses by expanding the first child node of the search tree that appears, searching progressively deeper until a target node is found, or until it encounters a node that has no children. The search then backtracks, returning to the most recent node it hasn’t finished exploring:

// Algorithm to recursively search network for paths
void DepthFirst( Network* network, 
                 std::vector<int>& visited, 
                 int end )
{
    int back = visited.back();

    std::vector< int > adjNode = network->GetAdjNodeIDs( back );

    // Examine adjacent nodes
    for ( std::vector<int>::iterator node_it = adjNode.begin();
          node_it != adjNode.end();
          node_it++ )
    {    
        int node = (*node_it);
        if ( ContainsNode( visited, node ) ) continue;

        if ( node == end )
        {
            visited.push_back( *node_it );
                        
            int hops = (int) visited.size();        

            for ( int i = 0; i < hops; i++ )
            {
                std::cout << visited[ i ] << " ";
            }
            std::cout << std::endl;
                                
            int n = (int) visited.size() - 1;
            visited.erase( visited.begin() + n );

            break;
        }            
    }

    // in breadth-first, recursion needs to come after visiting adjacent nodes
    for ( std::vector<int>::iterator node_it = adjNode.begin();
          node_it != adjNode.end();
          node_it++ )
    {
        int node = (*node_it);

        if ( ContainsNode( visited, node ) || node == end )        
            continue;
        
        visited.push_back( node );

        DepthFirst( network, visited, end );        

        int n = (int) visited.size() - 1;                
        visited.erase( visited.begin() + n );
    }       
}

Example 1: A Directed Graph

Here is the graphical representation of a 5-node directed graph. For example, a directed edge exists between nodes [1,3], but not nodes [3,1], hence the single arrow between the node [1,3] pair:

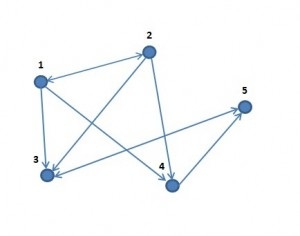
In the main program loop, the network was set to having directed edges, i.e., the bi-direction status is set to false. Individual links are inserted by using calls to the Network object’s AddLink method:

nw.SetBiDirection( false );

nw.AddLink( 1, 2 );  
nw.AddLink( 1, 3 );  
nw.AddLink( 1, 4 );  
nw.AddLink( 2, 1 );  
nw.AddLink( 2, 4 );  
nw.AddLink( 2, 3 );  
nw.AddLink( 3, 5 );  
nw.AddLink( 4, 5 );  
nw.AddLink( 5, 3 );

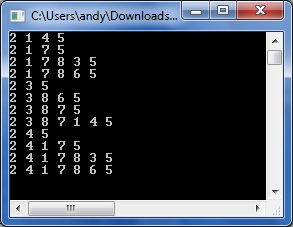
To find all the possible combinations of paths between nodes [2,5] for example, we simply specify the start and target nodes and feed the DepthFirst method with them:

int start  = 2;
int target = 5;

std::vector<int> visited;    
visited.push_back( start );
DepthFirst( &nw, visited, target );

To give the following output showing all combinations of paths between nodes 2 and 5:

Example 2: Bi-Directional Links

Here is a graphical representation of an 8 node network containing non-directed (bi-directional) links only. For bi-directional links, I dispense with the use of links with arrows for clarity, since traffic in both directions would be permissible:

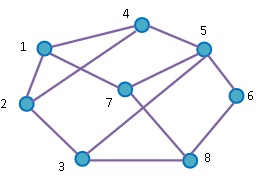
When creating networks with bi-directional links only, the bi-direction status is set to true before creating the desired topology using the AddLink method. If a link has already been added between (say) nodes 1 to 2, then adding a link from nodes 2 to 1 will not create an additional link, since it would have been deemed to already exist:

nw.SetBiDirection( true );

nw.AddLink( 1, 2 );  
nw.AddLink( 2, 1 );  // Makes no difference
nw.AddLink( 1, 4 );  
nw.AddLink( 1, 7 );  
nw.AddLink( 2, 4 );  
nw.AddLink( 2, 3 );  
nw.AddLink( 3, 5 );  
nw.AddLink( 3, 8 );  
nw.AddLink( 4, 5 ); 
nw.AddLink( 5, 6 );  
nw.AddLink( 5, 7 );
nw.AddLink( 6, 8 );  
nw.AddLink( 7, 8 );

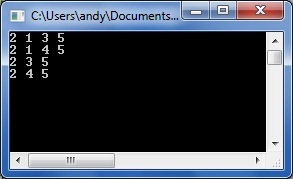
to give the following output showing all possible combinations of paths between nodes 2 and 5 for this 8-node network containing bi-directional links only: