Table of Contents
Introduction
In this article, we will explore vectorizing the pixel alphablending code in my earlier article. I believe most C/C++ programmers have tinkered with SIMD instructions like MMX and Streaming SIMD Extensions 2 (SSE) or even Advanced Vector Extensions (AVX). Most programmers, I believe, gave up after their first SIMD attempt, after that effort produced a mediocre or worse performance than the original non-vectorizing code. The main reason for slow performance is CPU cycles are typically wasted in packing the primitive data into a vector prior to SIMD execution and unpacking them into their proper place in the structure after execution. We will dive deeper into this in the next section. The main reason that SIMD is slow to be adopted by programmers around the world is because SIMD code is harder to write and the resultant code, even with using intrinsics, is not readable and even less understandable.
In this article, we will only focus on SSE2; the reason being MMX is a 64 bit SIMD technology which does not offer significant speed up compared to SSE2 (mostly 128 bit SIMD from Intel) on today's 64-bit processors, and Advanced Vector Extensions (AVX) (256 bit SIMD from Intel) is not chosen for this article because not many mainstream users own these latest Intel processors that can exploit AVX: SSE2 has been around since 2001. (Okay, I admit, the real reason is actually because I do not own an AVX supported processor. I promise to update the article when I have access to a PC with AVX-enabled processor.) All, but the oldest, personal computers should have housed a x86/x64 processor which supports SSE2. Rather than using inline assembly code, we will use SSE2 intrinsics provided by Visual Studio to assist us in calling the SSE2 instructions: currently, the Microsoft 64 bit C/C++ compiler does not permit inline assembly code.
Structure of Arrays
Let us imagine we have a structure type named SomeStruct as shown below and we have an array of SomeStruct, essentially, an array of structures.
struct SomeStruct
{
int aInteger;
double aDouble;
short aShort;
};
To use SSE2 arithmetic instructions on aInteger, we must first pack four aInteger into a 128 bit vector of integer type, __m128i.
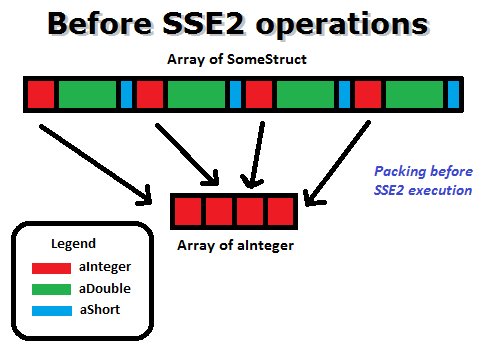
After we have got the computation result, we must unpack the four aIntegers into the individual structure objects in the array.

This is usually what kills the performance! To enhance performance, programmers are advised to pack their data into a structure of arrays rather than an array of structures; the same advice is applicable to GPGPU programming so as to allow memory coalescing. It is often not possible to alter the existing data domain/model to unnaturally suit the SIMD data packing requirement. In the structure shown below, arrInteger, arrDouble, and arrShort are usually pointers to dynamic allocated arrays whose size is only known during runtime, but I show them here to be of array type so as to emphasize they are of array type rather than pointer type.
struct SomeStruct
{
int arrInteger[1000];
double arrDouble[1000];
short arrShort[1000];
};
As the reader may have noticed, integer, double, and short data types have different sizes. Four integers would fit into __m128i and two doubles would fit into __m128i, and eight shorts would fit into __m128i. This might present difficulties when the programmer is writing code to loop through the __m128i arrays to do computation. For our case, this is not a problem, because we are only using the unsigned short type in this alphablend article.

Explanation of the Code
For our SSE2 alphablend code, we will, as I have just said, use the unsigned short type to store each color channel. The reader may ask why use unsigned short to store a value which only ranges from 0 to 255? The answer is due to the multiplication used, the intermediate values would most likely exceed 255 while the final result will still stay within 255. In normal coding, we can use byte variables to do the same computation, without using a 16-bit variable. The reason is because the byte value is automatically promoted to integer (native word size of the platform) before any computation takes place and is also automatically converted back to byte after computation. We have declared a __m128i array to store the unsigned short for each color channel of the two alphablending images. m_fullsize is to store the full size of the array in bytes. m_arraysize is the array size in terms of an 128-bit sized element. m_remainder is to hold the number to indicate which of the unsigned shorts are valid in the last 128-bit element if the number of unsigned shorts required is not cleanly divisible by 8 (8 x 16 bits = 128-bits). For example, four integers fit into __m128i; if we have six integers to compute, an array of two __m128i elements is needed but on the last __m128i element, only two integers is used, thus m_remainder would reflect 2.
__m128i* m_pSrc1R;
__m128i* m_pSrc1G;
__m128i* m_pSrc1B;
__m128i* m_pSrc2R;
__m128i* m_pSrc2G;
__m128i* m_pSrc2B;
int m_fullsize;
int m_arraysize;
int m_remainder;
With the GetUShortElement method, we can get an unsigned short element from the __m128i array, using an index which counts in terms of unsigned short elements.
unsigned short& CAlphablendDlg::GetUShortElement(
__m128i* ptr,
int index)
{
int bigIndex = index>>3;
int smallIndex = index - (bigIndex<<3);
return ptr[bigIndex].m128i_u16[smallIndex];
}
With the Get128BitElement method, we can get the __m128i element from the __m128i array, using a bigIndex which counts in terms of __m128i elements. bigSize is the size of the __m128i array in 128-bit chunks. smallRemainder is the number of valid unsigned short element in the last __m128i element. When we detect that it is the last element and the number of short integers is not clearly divisible by 8, we need to set the unused shorts in the last __m128i element to 1s, so as to prevent a division-by-zero error. It is a good practice to do this for every last element returned, regardless if it is integer type or float type.
__m128i& CAlphablendDlg::Get128BitElement(
__m128i* ptr,
int bigIndex,
int bigSize,
int smallRemainder)
{
if(bigIndex != bigSize-1) return ptr[bigIndex];
else if(smallRemainder==0) return ptr[bigIndex];
else {
for(int i=smallRemainder; i<8; ++i)
ptr[bigIndex].m128i_u16[i] = 1;
return ptr[bigIndex];
}
}
We must take care to allocate our __m128i array with the _aligned_malloc function so that they would align with a 16 bytes boundary as required by the 128-bit SSE2 instructions. We calculate and store the remainder if the number of unsigned short required is not cleanly divisible by 8 (as explained before) (Note: there are 8 unsigned short (16 bit data type) in 128-bit.)
m_fullsize = m_BmpData1.Width * m_BmpData1.Height;
m_arraysize = (m_fullsize) >> 3;
m_remainder = m_fullsize%8;
if(m_remainder!=0)
++m_arraysize;
m_fullsize = (m_arraysize) * 8 * 2;
m_pSrc1R = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc1G = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc1B = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2R = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2G = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2B = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
After allocating our __m128i arrays, we will populate them with the color information from the image object. We use GetUShortElement to get our unsigned short element from the __m128i array.
UINT col = 0;
UINT stride = m_BmpData1.Stride >> 2;
for(UINT row = 0; row < m_BmpData1.Height; ++row)
{
for(col = 0; col < m_BmpData1.Width; ++col)
{
UINT index = row * stride + col;
BYTE r = (m_pPixels1[index] & 0xff0000) >> 16;
BYTE g = (m_pPixels1[index] & 0xff00) >> 8;
BYTE b = (m_pPixels1[index] & 0xff);
GetUShortElement(m_pSrc1R, (int)(index)) = r;
GetUShortElement(m_pSrc1G, (int)(index)) = g;
GetUShortElement(m_pSrc1B, (int)(index)) = b;
}
}
Lastly, we must remember to de-allocate the __m128i arrays with _aligned_free in the destructor of the parent class. It is a good practice to remember to write deallocation code before we begin our main coding.
if( m_pSrc1R )
{
_aligned_free(m_pSrc1R);
m_pSrc1R = NULL;
}
if( m_pSrc1G )
{
_aligned_free(m_pSrc1G);
m_pSrc1G = NULL;
}
if( m_pSrc1B )
{
_aligned_free(m_pSrc1B);
m_pSrc1B = NULL;
}
if( m_pSrc2R )
{
_aligned_free(m_pSrc2R);
m_pSrc2R = NULL;
}
if( m_pSrc2G )
{
_aligned_free(m_pSrc2G);
m_pSrc2G = NULL;
}
if( m_pSrc2B )
{
_aligned_free(m_pSrc2B);
m_pSrc2B = NULL;
}
Before we run any SSE2 code, we should ensure that SSE2 is supported on the processor first. We can use the SIMD Detector class, written by the author, to do the check.
#include "SIMD.h"
SIMD m_simd;
if(m_simd.HasSSE2()==false)
{
MessageBox(
"Sorry, your processor does not support SSE2",
"Error",
MB_ICONERROR);
return;
}
Now we have come to the meat of the article: using SSE2 to do alphablending. The formula used is ((SrcColor * Alpha) + (DestColor * InverseAlpha)) >> 8. The below code listing is heavily commented. We use the _mm_set1_epi16 instruction to set the same short value (0) in every short element in the __m128i element. The _mm_mullo_epi16 instruction is used to multiply the unsigned short and only retain the 16 bits if the final result overflows into 32 bits. We use the _mm_add_epi16 instruction for adding of unsigned shorts. The _mm_srli_epi16 instruction is to do shift right by 8 times to simulate division by 256. We can get away without using division instruction which is a blessing because SSE2 does not support division for integers. After SSE2 operations, we need to unpack the data back to ARGB format. This unpacking offsets some of the performance gains.
__m128i nAlpha128 = _mm_set1_epi16 ((short)(Alpha));
__m128i nInvAlpha128 = _mm_set1_epi16 ((short)(255-Alpha));
__m128i src1R = _mm_set1_epi16 ((short)(0));
__m128i src1G = _mm_set1_epi16 ((short)(0));
__m128i src1B = _mm_set1_epi16 ((short)(0));
__m128i src2R = _mm_set1_epi16 ((short)(0));
__m128i src2G = _mm_set1_epi16 ((short)(0));
__m128i src2B = _mm_set1_epi16 ((short)(0));
__m128i rFinal = _mm_set1_epi16 ((short)(0));
__m128i gFinal = _mm_set1_epi16 ((short)(0));
__m128i bFinal = _mm_set1_epi16 ((short)(0));
for(int i=0;i<m_arraysize;++i)
{
src1R = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1R,i,m_arraysize,m_remainder),
nAlpha128);
src1G = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1G,i,m_arraysize,m_remainder),
nAlpha128);
src1B = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1B,i,m_arraysize,m_remainder),
nAlpha128);
src2R = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2R,i,m_arraysize,m_remainder),
nInvAlpha128);
src2G = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2G,i,m_arraysize,m_remainder),
nInvAlpha128);
src2B = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2B,i,m_arraysize,m_remainder),
nInvAlpha128);
rFinal = _mm_add_epi16 (src1R, src2R);
gFinal = _mm_add_epi16 (src1G, src2G);
bFinal = _mm_add_epi16 (src1B, src2B);
rFinal = _mm_srli_epi16 (rFinal, 8);
gFinal = _mm_srli_epi16 (gFinal, 8);
bFinal = _mm_srli_epi16 (bFinal, 8);
int step = i << 3; if(i!=m_arraysize-1) {
pixels[step+0] =
0xff000000 |
rFinal.m128i_u16[0] << 16 |
gFinal.m128i_u16[0] << 8 |
bFinal.m128i_u16[0];
pixels[step+1] =
0xff000000 |
rFinal.m128i_u16[1] << 16 |
gFinal.m128i_u16[1] << 8 |
bFinal.m128i_u16[1];
pixels[step+2] =
0xff000000 |
rFinal.m128i_u16[2] << 16 |
gFinal.m128i_u16[2] << 8 |
bFinal.m128i_u16[2];
pixels[step+3] =
0xff000000 |
rFinal.m128i_u16[3] << 16 |
gFinal.m128i_u16[3] << 8 |
bFinal.m128i_u16[3];
pixels[step+4] =
0xff000000 |
rFinal.m128i_u16[4] << 16 |
gFinal.m128i_u16[4] << 8 |
bFinal.m128i_u16[4];
pixels[step+5] =
0xff000000 |
rFinal.m128i_u16[5] << 16 |
gFinal.m128i_u16[5] << 8 |
bFinal.m128i_u16[5];
pixels[step+6] =
0xff000000 |
rFinal.m128i_u16[6] << 16 |
gFinal.m128i_u16[6] << 8 |
bFinal.m128i_u16[6];
pixels[step+7] =
0xff000000 |
rFinal.m128i_u16[7] << 16 |
gFinal.m128i_u16[7] << 8 |
bFinal.m128i_u16[7];
}
else if(m_remainder!=0)
{
for(int smallIndex=0; smallIndex<m_remainder; ++smallIndex)
{
pixels[i+smallIndex] =
0xff000000 |
rFinal.m128i_u16[smallIndex] << 16 |
gFinal.m128i_u16[smallIndex] << 8 |
bFinal.m128i_u16[smallIndex];
}
}
else
{
pixels[step+0] =
0xff000000 |
rFinal.m128i_u16[0] << 16 |
gFinal.m128i_u16[0] << 8 |
bFinal.m128i_u16[0];
pixels[step+1] =
0xff000000 |
rFinal.m128i_u16[1] << 16 |
gFinal.m128i_u16[1] << 8 |
bFinal.m128i_u16[1];
pixels[step+2] =
0xff000000 |
rFinal.m128i_u16[2] << 16 |
gFinal.m128i_u16[2] << 8 |
bFinal.m128i_u16[2];
pixels[step+3] =
0xff000000 |
rFinal.m128i_u16[3] << 16 |
gFinal.m128i_u16[3] << 8 |
bFinal.m128i_u16[3];
pixels[step+4] =
0xff000000 |
rFinal.m128i_u16[4] << 16 |
gFinal.m128i_u16[4] << 8 |
bFinal.m128i_u16[4];
pixels[step+5] =
0xff000000 |
rFinal.m128i_u16[5] << 16 |
gFinal.m128i_u16[5] << 8 |
bFinal.m128i_u16[5];
pixels[step+6] =
0xff000000 |
rFinal.m128i_u16[6] << 16 |
gFinal.m128i_u16[6] << 8 |
bFinal.m128i_u16[6];
pixels[step+7] =
0xff000000 |
rFinal.m128i_u16[7] << 16 |
gFinal.m128i_u16[7] << 8 |
bFinal.m128i_u16[7];
}
}
Benchmark Results

Below are listed the formulae used in each benchmark:
Unoptimized code formula used

Optimized code formula used

Optimized code with shift formula used

SSE2 optimized code formula used

This is the timing of doing alphablending 1000 times on an Intel i7 870 at 2.93 Ghz. The performance characteristic is different from what is posted in the earlier article because the benchmarks are done on different PCs. The earlier PC used has 'retired' from useful service in this world.

VS2010 Release mode(optimization disabled)(Lower is better)
Author code
Unoptimized Code : 4679 milliseconds
Optimized Code : 2108 milliseconds
Optimized Code with Shift : 1931 milliseconds
SSE2 Optimized Code : 862 milliseconds (works for all image width)
Yves Daoust's code
C version : 1923 milliseconds
MMX 1 : 1888 milliseconds
MMX 2 : 1355 milliseconds (image width must be even)
SSE : 762 milliseconds (image width must be multiple of 4)
VS2010 Release mode(optimization enabled)(Lower is better)
Author code
Unoptimized Code : 3324 milliseconds
Optimized Code : 1378 milliseconds
Optimized Code with Shift : 802 milliseconds
SSE2 Optimized Code : 406 milliseconds (works for all image width)
Yves Daoust's code
C version : 604 milliseconds
MMX 1 : 213 milliseconds
MMX 2 : 167 milliseconds (image width must be even)
SSE : 104 milliseconds (image width must be multiple of 4)
Below is the number of times of speedup we got when compared to the unoptimized version. But comparing the SSE2 speedup to the second runner up (Optimized Code with Shift), the speedup is only 2.2 times, not the 8 times as we have expected. So what is the memory consumption needed for this SSE2 speedup? 2 bytes for each color channel instead of 1 byte. The original implementation needs 4 bytes to store a color pixel, ARGB. (4 bytes is used because the processor can load and store 32 bit data faster than 24 bit data, which may require shifting it to proper 32 bit boundary before loading inside the 32 bit register). The SSE2 version needs 6 bytes to store a color pixel, RGB (because two bytes are used to store each color channel). Individual alpha channels are not stored because they are not used. The SSE2 version would need 50% more of memory to perform its magic.
(Higher is better)
Unoptimized Code : 1x
Optimized Code : 2.2x
Optimized Code with Shift : 2.4x
SSE2 Optimized Code : 5.4x
Conclusion
We have used SSE2 to speed up from the previous fastest performance by two times. The speedup is not dramatic. It is probably not worth the amount of extended effort and unreadable code to do this. To achieve better readability, we could use the vector class listed in the dvec.h header. This vector class supports overloaded operators for -, +, *, /, and so on. Any suggestion to improve the performance further is welcome. We could ramp up performance by using OpenMP or Parallel Patterns Library (PPL) in tandem with SSE2. But that is an article for another day. Any reader interested in a future article about utilizing OpenCL to do alphablending, please drop me a message below. OpenCL is a heterogeneous technology; OpenCL kernel can be run on either CPUs or GPUs.
References
History
- 17th Nov 2011 : Added Yves Daoust's MMX and SSE code and benchmark results
- 14th Nov 2011 : Initial Release
