Tip: To use the program, set the desired parameters by using the Settings sub-menu, and then initialize the appropriate type.
Introduction
The project aims at developing a program which could demonstrate and simulate Artificial Life. The project implements three main technologies which are used in the Gaming industry and Robotics for coding intelligent agents. These are:
- Neural Networks
- Genetic Algorithms
- Steering Behaviours
The project will implement each of these, and demonstrate their usefulness in creating Intelligent Agents.
The algorithms demonstrated are the core of almost every game. The direct consequence of the project's capabilities will allow it to be used as a tool for understanding various techniques for creating Intelligent Agents. An improved version, suited for particular needs, could be used for training real robots for real applications such as Patrolling, Finding Landmines, Evolving, and others. The project can also be used as a means of studying evolution. Further, the project will allow creation of games that feature Intelligent Agents.
Applications:
- Game Development
- Simulator Development
- Machine Learning
- Intelligent Toys
Background
Neural Networks
An artificial neural network (ANN), often just called a "neural network" (NN), is a mathematical model or computational model based on biological neural networks. It consists of an interconnected group of artificial neurons, and processes information using a connectionist approach to computation. In most cases, an ANN is an adaptive system that changes its structure based on external or internal information that flows through the network during the learning phase.
In more practical terms, neural networks are non-linear statistical data modeling tools. They can be used to model complex relationships between inputs and outputs, or to find patterns in data.
Perhaps, the greatest advantage of ANNs is their ability to be used as an arbitrary function approximation mechanism which 'learns' from observed data. However, using them is not so straightforward, and a relatively good understanding of the underlying theory is essential.
- Choice of model: This will depend on the data representation and the application. Overly complex models tend to lead to problems with learning.
- Learning algorithm: There are numerous tradeoffs between learning algorithms. Almost any algorithm will work well with the correct type of parameters for training on a particular fixed dataset. However, selecting and tuning an algorithm for training on unseen data requires a significant amount of experimentation.
- Robustness: If the model, cost function, and learning algorithm are selected appropriately, the resulting ANN can be extremely robust.
With the correct implementation, ANNs can be used naturally in online learning and large dataset applications. Their simple implementation and the existence of mostly local dependencies exhibited in the structure allows for fast, parallel implementations in hardware.
Genetic Algorithms
A genetic algorithm (GA) is a search technique used in computing to find exact or approximate solutions to optimization and search problems. Genetic algorithms are categorized as global search heuristics. Genetic algorithms are a particular class of evolutionary algorithms (also known as evolutionary computation) that use techniques inspired by evolutionary biology such as inheritance, mutation, selection, and crossover (also called recombination).
Genetic algorithms are implemented as a computer simulation in which a population of abstract representations (called chromosomes, or the genotype, or the genome) of candidate solutions (called individuals, creatures, or phenotypes) to an optimization problem evolves towards better solutions. Traditionally, solutions are represented in binary as strings of 0s and 1s, but other encodings are also possible.
The evolution usually starts from a population of randomly generated individuals, and happens in generations. In each generation, the fitness of every individual in the population is evaluated, multiple individuals are stochastically selected from the current population (based on their fitness), and modified (recombined, and possibly randomly mutated) to form a new population. The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. If the algorithm has terminated due to a maximum number of generations, a satisfactory solution may or may not have been reached.
Genetic algorithms find application in Bioinformatics, Phylogenetics, Computer Science, Engineering, Economics, Chemistry, Manufacturing, Mathematics, Physics, and other fields.
Steering Behaviours
Steering Behaviours present solutions for one requirement of autonomous characters in animation and games: the ability to navigate around their world in a life-like and improvisational manner. These Steering Behaviours are largely independent of the particulars of the character’s means of locomotion. Combinations of steering behaviours can be used to achieve higher level goals (for example: get from here to there while avoiding obstacles, follow this corridor, join that group of characters...).
Autonomous characters are a type of autonomous agents intended for use in computer animation and interactive media such as games and virtual reality. These agents represent a character in a story or game, and have some ability to improvise their actions. This stands in contrast both to a character in an animated film, whose actions are scripted in advance, and to an “avatar” in game or virtual reality, whose actions are directed in real time by a human player or participant. In games, autonomous characters are sometimes called non-player characters. An autonomous character must combine aspects of an autonomous robot with some skills of a human actor in improvisational theater. These characters are usually not real robots, and are certainly not human actors, but share some properties of each.
The term behaviour has many meanings. It can mean the complex action of a human or other animal based on volition or instinct. It can mean the largely predictable actions of a simple mechanical system, or the complex action of a chaotic system. In virtual reality and multimedia applications, it is sometimes used as a synonym for “animation”. Here, the term behaviour is used to refer to the improvisational and lifelike actions of an autonomous character.
Design
The project has three sub-projects, namely:
- Steering Behaviours
- EStrings
- Ants
The organization of classes in the project is depicted below:
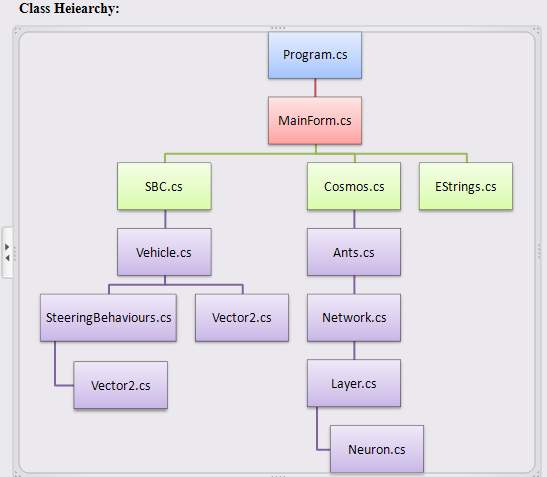
The image above describes how classes are related to each other, and not inheritance. In brief, the MainForm class possesses objects of SBC (Steering Behaviours Controller), Cosmos and EStrings (Evolving Strings). MainForm uses them to manage the program.
Here, SBC creates objects of the Vehicle class; each Vehicle has access to the SteeringBehaviours class, which it uses to determine the force (direction as well as speed) which is to be applied to itself under the present behaviour. SteeringBehaviours and Vehicle, both use Vector for vector calculations.
The Cosmos class represents a world for the ants in it. It is the paint area of the panel. The Cosmos class creates objects of Ants; Ants in turn create objects of Network (their brain), which they use to determine position, speed, and rotation.
The EStrings class is a simple demonstration of Genetic Algorithms and how they can be used to converge to the solution. Here, the target is a string, but in reality, it can be anything that can be represented in a computer. Try to find how many generations it takes for your name to evolve!
Using the Code
Now, I will explain each one in detail. The first one is:
Steering Behaviours
Steering Behaviours, in short, is a way to move your autonomous game agent so that it looks as if it has brains. Almost every game uses them to produce human like behaviour. But in reality, there is nothing intelligent about it, it's just an illusion, it's all mathematical. I have implemented the following behaviours:
| Behaviour Name | Description |
1. Seek | The Seek Steering Behaviour returns a force that directs an agent towards a target position. |
2. Flee | The Flee Steering Behaviour returns a force that directs an agent away from the target position. |
3. Arrive | Arrive is a behaviour that steers the agent in such a way it decelerates onto the target position. |
4. Wander | Wander is a behaviour that steers the agent in a random way with no target position. |
5. PathFollowing | PathFollowing creates a steering force that moves a vehicle along a series of waypoints, forming a path. |
6. Cohesion | Cohesion produces a steering force that moves a vehicle toward the center of mass of its neighbors. |
7. Alignment | Alignment attempts to keep a vehicle's heading aligned with its neighbors. |
8. Separation | Separation creates a force that steers a vehicle away from those in its neighborhood region. |
Description
Steering Behaviours use the following model as a basis for simulating various behaviours.

Refer to this article for more details.
A simple vehicle model:
| Variable | Type |
mass | scalar |
position | vector |
velocity | vector |
max_force | scalar |
max_speed | scalar |
Represented here by:
private float mass;
private int max_speed, max_force, vehicleNo;
private Vector2 currentPosition, velocity, acceleration,
heading, steerForce, targetPosition;
These variables maintain data about the current state of the vehicle. These are used by the Steering Behaviour's functions to calculate force. I think all of them are self-explanatory. This force is then used to determine the vehicle's new position, velocity, acceleration, and heading. Now, after obtaining the new values, these are then again used to calculate new ones! And, the cycle continues. This cycle updates the vehicle's position continuously as described by the Steering Behaviour.
The following lines of code demonstrate exactly how to do it. Here, steerForce and velocity are truncated because in real life, vehicles do have their limits. A little change of max_force, max_speed, and mass can make all the difference between the best sports car and the worst (provided you are using this in a racing game; it might seem weird, but that is all there is to it!).
steerForce = Vector2.Truncate(steerForce, max_force);
acceleration = steerForce / mass;
velocity = Vector2.Truncate(velocity + acceleration, max_speed);
currentPosition = Vector2.Add(velocity, currentPosition);
1. Seek
Now, let's talk about Seek! It is the simplest of all behaviours to understand and code. Here's the code:
public static Vector2 Seek(ref Vector2 targetPosition, ref Vector2 currentPosition,
ref Vector2 Velocity, int max_speed)
{
Vector2 desired_V = Vector2.Normalize(
Vector2.Subtract(targetPosition, currentPosition)) * max_speed;
return Vector2.Subtract(desired_V, Velocity);
}
First, the desired velocity is calculated. This is the velocity the agent would need to reach the target position in an ideal world. It represents the vector from the agent to the target, scaled to be the length of the maximum possible speed of the agent.
The steering force returned by this method is the force required, which when added to the agent's current velocity vector gives the desired velocity. To achieve this, you simply subtract the agent's current velocity from the desired velocity.
And, here is the effect it has on 100 game agents (I made them to look like police vehicles, maybe they are chasing a criminal!).

And yes, by using the keys, about which the top-left corner tells, you can control the first vehicle's variables in real-time and see how it affects the vehicle's behavior. The ones highlighted in green are general, and the ones highlighted in yellow are specific to a particular Steering Behavior.
2. Flee
Now, the Flee. It is completely opposite to Seek. Here, we subtract targetPosition from currentPosition, rather than currentPosition from targetPosition. Here is the code (look at the else part):
public static Vector2 Flee(Graphics g,ref Vector2 targetPosition,
ref Vector2 currentPosition, ref Vector2 Velocity,
int max_speed, int FOV,int vehicleNo)
{
if (mainForm.steeringBehaviour != SB.CF && mainForm.steeringBehaviour !=
SB.FCS && mainForm.steeringBehaviour != SB.FCAS && vehicleNo ==1)
{
g.DrawEllipse(Pens.Red, new RectangleF(new PointF(targetPosition.X - FOV,
targetPosition.Y - FOV), new SizeF(FOV*2, FOV*2)));
}
if (Vector2.Length(Vector2.Subtract(targetPosition, currentPosition)) > FOV)
{
return None();
}
else
{
Vector2 desired_V = Vector2.Normalize(Vector2.Subtract(
currentPosition, SBC.targetPosition)) * max_speed;
return Vector2.Subtract(desired_V, Velocity);
}
}
Now, you want to know what the other code is about. Well, I must tell you that there are a lot of different implementations possible for Steering Behaviours; some are simple, and some are more complex. This one uses a concept of FOV (Field of View) i.e., the area that is visible to the agent. This makes the agent respond by fleeing if it can see the danger. (It totally makes sense; in real life, every agent has limited FOV, e.g., a deer will run if it sees the lion (i.e., if the lion is in its FOV)) So simple! Now, the first if() is about whether to show/draw the FOV or not. The next if() determines whether to flee or not (i.e., is the threat in the FOV?).
Here's how 100 agents react when they are scared! Notice that you can change the FOV by using the Y and H keys.

3. Arrive
Now comes Arrive. Seek is useful for getting an agent moving in the right direction, but often, you'll want your agents to come to a gentle halt at the target position, and as you've seen, Seek is not too great at stopping gracefully. Arrive is a behavior that steers the agent in such a way it decelerates onto the target position.
Here's the code (watch for arriveRadius):
public static Vector2 Arrive(Graphics g,ref Vector2 targetPosition,
ref Vector2 currentPosition,ref Vector2 Velocity,
int arriveRadius, int max_speed,int vehicleNo)
{
if (vehicleNo == 1)
{
g.DrawEllipse(Pens.SkyBlue, new RectangleF(
new PointF(targetPosition.X - arriveRadius,
targetPosition.Y - arriveRadius),
new SizeF(arriveRadius * 2, arriveRadius * 2)));
}
Vector2 toTarget = Vector2.Subtract(targetPosition, currentPosition);
double distance = toTarget.Length();
if (distance > 0)
{
double speed = max_speed * (distance / arriveRadius);
speed = Math.Min(speed, max_speed);
Vector2 desired_V = toTarget * (float)(speed/distance);
return Vector2.Subtract(desired_V, Velocity);
}
return new Vector2(0, 0);
}
Don't get confused by the use of the if() statement; it is there so that only one vehicle draws the arrive radius and not all. This improves performance, and is also logical since there's no point in 100 circles on top of one another. Here, (distance / arriveRadius) causes a steady decrease in speed as the vehicle approaches its target position, and it eventually stops.
Here's how 100 vehicles look when they are parked! Or maybe, they are people discussing something! The exact uses of this and other Steering Behaviours depend on the game; it all depends upon the imagination of the designer.

4. Wander
Now, it will be Wander. Wander is a type of random steering. One easy implementation would be to generate a random steering force in each frame, but this produces rather uninteresting motion. It is twitchy, and produces no sustained turns. A more interesting approach is to retain the steering direction state and make small random displacements to it in each frame. Thus, at one frame, the character may be turning up and to the right, and on the next frame, it will still be turning in almost the same direction. The steering force takes a random walk from one direction to another. To produce the steering force for the next frame, a random displacement is added to the previous value, and the sum is constrained again to the sphere’s surface. The sphere’s radius (the large circle) determines the maximum wandering strength, and the magnitude of the random displacement (the small circle) determines the wander rate.
Here's the code:
public static Vector2 Wander(Graphics g, ref Vector2 wanderTarget,
ref Vector2 currentPosition, ref Vector2 Velocity, ref Vector2 heading,
float wanderRadius, float wanderDistance, int wanderJitter)
{
heading = Vector2.Normalize(Velocity);
wanderTarget += new Vector2(random.Next(-wanderJitter, wanderJitter),
random.Next(-wanderJitter, wanderJitter));
wanderTarget = Vector2.Normalize(wanderTarget);
wanderTarget *= wanderRadius / 2;
PointF circleCenterG = new PointF((heading.X * wanderDistance + currentPosition.X) -
wanderRadius / 2, (heading.Y * wanderDistance +
currentPosition.Y) - wanderRadius / 2);
Vector2 circleCenterM = new Vector2((heading.X * wanderDistance) + currentPosition.X,
(heading.Y * wanderDistance) + currentPosition.Y);
Vector2 pointOnCircle = new Vector2(circleCenterM.X + wanderTarget.X,
circleCenterM.Y + wanderTarget.Y);
g.DrawEllipse(Pens.LightGreen, new RectangleF(new PointF(circleCenterG.X,
circleCenterG.Y), new SizeF(wanderRadius, wanderRadius)));
g.FillEllipse(Brushes.LightYellow, new RectangleF(new PointF(
pointOnCircle.X - 4, pointOnCircle.Y - 4), new SizeF(8, 8)));
return Vector2.Subtract(pointOnCircle, currentPosition);
}
And, here's how it looks:

And, with "Leave Trail" on:

What the leave trail does is that it lets you see that the path traveled was indeed random and smooth. Mission accomplished! Don't forget to play with the variables in the top-left corner.
5. PathFollowing
Next is PathFollowing. PathFollowing creates a steering force that moves a vehicle along a series of waypoints, forming a path. Sometimes, paths have a start and end point, and at other times, they loop back around on themselves forming a never-ending, closed path.
You'll find countless uses for using paths in your game. You can use them to create agents that patrol important areas of a map, to enable units to traverse difficult terrain, or to help racing cars navigate around a racetrack. They are useful in most situations where an agent must visit a series of checkpoints.
The simplest way of following a path is to set the current waypoint to the first in the list, steer towards that using Seek until the vehicle comes within a target distance of it, then grab the next waypoint and Seek to that, and so on, until the current waypoint is the last waypoint in the list. When this happens, the vehicle should either arrive at the current waypoint, or, if the path is a closed loop, the current waypoint should be set to the first in the list again, and the vehicle just keeps on Seeking.
Here's the code for PathFollowing:
public static Vector2 PathFollowing(ref Vector2 targetPosition,
ref Vector2 currentPosition, ref Vector2 Velocity,
ref Point[] pathPoints, ref int currentPathPoint,
int maxPathPoints, int max_speed)
{
if (currentPathPoint > maxPathPoints - 1)
{
currentPathPoint = 0;
}
int nextPathPoint = currentPathPoint + 1;
if ((nextPathPoint > (maxPathPoints - 1)))
{
nextPathPoint = 0;
}
Vector2 currentPath = new Vector2(pathPoints[currentPathPoint].X,
pathPoints[currentPathPoint].Y);
Vector2 differenceV = Vector2.Subtract(currentPosition, currentPath);
if (Math.Abs(differenceV.Length()) < 5)
{
targetPosition = new Vector2(pathPoints[nextPathPoint].X,
pathPoints[nextPathPoint].Y);
++currentPathPoint;
return Seek(ref targetPosition, ref currentPosition, ref Velocity,max_speed);
}
else
{
targetPosition = new Vector2(pathPoints[currentPathPoint].X,
pathPoints[currentPathPoint].Y);
return Seek(ref targetPosition, ref currentPosition, ref Velocity,max_speed);
}
}
Tip: Decrease the max_speed to see a soldier patrolling, and increase it to see a racing car going through check points!
And, here's an agent following a path:

6. Separation
Next comes Separation. The Separation Steering Behavior gives a character the ability to maintain a certain separation distance from others nearby. This can be used to prevent characters from crowding together. To compute steering for Separation, first a search is made to find other characters within the specified neighborhood. This might be an exhaustive search of all characters in the simulated world, or might use some sort of spatial partitioning or caching scheme to limit the search to local characters. For each nearby character, a repulsive force is computed by subtracting the positions of our character and the nearby character, normalizing, and then applying a 1/r weighting. (That is, the position offset vector is scaled by 1/r 2.) Note that 1/r is just a setting that has worked well, not a fundamental value. These repulsive forces for each nearby character are summed together to produce the overall steering force.
Here's the code:
public static Vector2 Separation(ref Vehicle[] allCars, Vehicle me,
ref Vector2 currentPosition, ref Vector2 velocity, int max_speed)
{
int j = 0;
Vector2 separationForce = new Vector2(0);
Vector2 averageDirection = new Vector2(0);
Vector2 distance = new Vector2(0);
for (int i = 0; i < allCars.Length; i++)
{
distance = Vector2.Subtract(currentPosition, allCars[i].CurrentPosition);
if (Vector2.Length(distance) < 100 && allCars[i] != me)
{
j++;
separationForce += Vector2.Subtract(currentPosition,
allCars[i].CurrentPosition);
separationForce = Vector2.Normalize(separationForce);
separationForce = Vector2.Multiply(separationForce, 1 / .7f);
averageDirection = Vector2.Add(averageDirection, separationForce);
}
}
if (j == 0)
{
return None();
}
else
{
return averageDirection;
}
}
And, here's how it looks (that's what happens when every one tries to find a quiet place for oneself in such a crowded world!):

7. Cohesion
Next is Cohesion. The Cohesion Steering Behavior gives a character the ability to cohere with (approach and form a group with) other nearby characters. Steering for Cohesion can be computed by finding all the characters in the local neighborhood (as described above for Separation) and computing the average position (or center of gravity) of the nearby characters. The steering force can be applied in the direction of that average position, or it can be used as the target for seek Steering Behavior.
Here's the code:
public static Vector2 Cohesion(ref Vehicle[] allCars,Vehicle me,
Vector2 currentPosition, Vector2 velocity,
int max_speed, int cohesionRadius)
{
int j = 0;
Vector2 averagePosition = new Vector2(0);
Vector2 distance = new Vector2(0);
for (int i = 0; i < allCars.Length; i++)
{
distance = Vector2.Subtract(currentPosition, allCars[i].CurrentPosition);
if (Vector2.Length(distance) < cohesionRadius && allCars[i] != me)
{
j++;
averagePosition = Vector2.Add(averagePosition, allCars[i].CurrentPosition);
Vector2.Normalize(distance) / Vector2.Length(distance));
}
}
if (j == 0)
{
return None();
}
else
{
averagePosition = averagePosition / j;
return Seek(ref averagePosition, ref currentPosition,
ref velocity, max_speed);
}
}
Tip: Play with the cohesion radius and see its effect on the number of groups. And, it looks like (Notice how groups are forming, are they forming gangs? Oh my!):

Also, try to think of uses of such a behaviour (who would want to form a group?).
8. Alignment
Next is Alignment. The Alignment Steering Behavior gives a character the ability to align itself with (that is, head in the same direction and/or speed as) other nearby characters. Steering for alignment can be computed by finding all characters in the local neighborhood (as described above for Separation) and averaging together the velocity (or alternately, the unit forward vector) of the nearby characters. This average is the desired velocity, and so the steering vector is the difference between the average and our character’s current velocity (or alternately, its unit forward vector). This steering will tend to turn our character so it is aligned with its neighbors.
Here's the code:
public static Vector2 Alignment(ref Vehicle[] allCars, Vehicle me,
ref Vector2 currentPosition, ref Vector2 velocity, int max_speed)
{
int j = 0;
Vector2 averageDirection = new Vector2(0);
Vector2 distance = new Vector2(0);
for (int i = 0; i < allCars.Length; i++)
{
distance = Vector2.Subtract(currentPosition, allCars[i].CurrentPosition);
if (Vector2.Length(distance) < 100 && allCars[i] != me)
{
j++;
averageDirection = Vector2.Add(averageDirection, allCars[i].Velocity);
}
}
if (j == 0)
{
return None();
}
else
{
averageDirection = averageDirection / j;
return Vector2.Subtract(averageDirection, velocity);
}
}
And, here's how it looks like (Have you ever seen birds flying? What will you do if you want to incorporate such a behavior in your own game?):

Many of interesting behaviors seen in games is not produced by a single behavior, but by a combination of many. How the forces of all the behaviors are combined depends upon the problem. Here, I demonstrate one such combination of Flee, Separation, Cohesion, and Alignment (FCAS).
What happens to the agents when all FCAS forces are applied at the same time? Well, every agent will try to flee from a target (F), try to form a group (C), move in the direction of others (A), and demand its own private space also (S). It really is interesting to watch such a combination.
The image below has a vehicle set to wander behavior, and all others see this vehicle as a threat and implement the FCAS behavior. It looks like a lion is chasing a herd of cattle, or maybe the shark is after small fish! It all depends upon one's imagination.

That concludes Steering Behaviors. There are a lot more possible steering behaviors, but they involve matrix calculations and are more complex, but much more interesting to watch; you may also want to try them!
EStrings
EStrings will help people new to GA (Genetic Algorithms) understand GA better. GA is a search-for-solution technique, it is used to find solutions to problems about which not much is known, or where traditional techniques of calculus and others fail or are too inefficient. This implementation of GA tries to converge to a string from some randomly generated strings. GA is based on Darwin's theory of evolution, and therefore things like Mutation, Crossover, Fitness, Parents, etc., are used, which are not found in typical applications.
In games, GAs are used to train neural networks, which are typically the brain of the agent. So, we use GAs to find an "optimal state of brain" for the agent so that it works better, or adjusts to the environment, etc. Though this implementation may not be of any direct use, for a beginner, it's a sound take-off. It may surprise some, but GAs can be used for almost any problem, any that can be represented in a computer and we know how to evaluate a solution for.
The first step is to represent the problem. Since here we are converging to a string, a string is the best representation. Next, we generate random population (here, of strings). Each string is called a chromosome, and each character represents a characteristic of the organism.
static void Initialize(ref List<OneString> ones, ref List<OneString> two,
ref List<OneString> temp)
{
string rString = "";
for (int i = 0; i < popSize; i++)
{
rString = "";
for (int j = 0; j < sLen; j++)
{
rString += (char)rand.Next(32, 142);
}
ones.Add(new OneString(rString, 0));
two.Add(new OneString(rString, 0));
temp.Add(new OneString(rString, 0));
}
Look how we are generating random characters between ASCII 32 and 142. A permutation of this constitutes our search space. Since our target string has to evolve from the present generation, it is good to have a large population, so that our chances for finding the particular characteristic (here, a character) are good. After generating a good enough population, we evaluate them and try to find the top; this is done using the fitness function:
private static void CalculateFitness(ref List<OneString> ones)
{
int fitness;
for (int i = 0; i < popSize; i++)
{
fitness = 0;
for (int j = 0; j < sLen; j++)
{
fitness += Math.Abs(ones[i].name[j] - target[j]);
}
ones[i].fitness = fitness;
}
}
Here, the absolute value of ASCII difference between the target and a string from the population is the error. If this error is zero, this means we have found a solution and the search stops. If not, we generate a new generation using mutation, elitism, crossover, etc., and repeat the process with the new generation.
Here's how it looks:

Ants
This is the last part of this project, it will combine GAs with NNs (Neural Networks). Here, we create ants that can learn how to find food! We first create a lot of ants (using a typical ant model), give them their brain (the NN, each ant has its own), feed the data about its current motion into the network, get the outputs, and use them to move them again (hopefully closer to food). We do this for some time, and then we see which ant got the most food using its brain (the NN). A GA fitness function is used for evaluation. After evaluation, we sort them in some order, choose the best ones, let them be parents and have children. We loop until ants actually learn.
The NN is represented by a list of numbers (Notice that in EStrings, it was a list of characters, and here it's a list of numbers), these numbers make up the weight of the NN. The solution space is again the permutation of them, and the problem is to find the combination which will steer an ant towards the nearest food.
The image below shows the network's basic structure:

private void Update()
{
int totalFit = CalculateFitness();
PrintBest(totalFit);
lastTotalFit = totalFit;
NewGeneration();
inCG = 0;
generationCount++;
}
The above method shows the step method used, and below is the fitness method.
private int CalculateFitness()
{
int totalFit = 0;
for (int i = 0; i < numAnts; i++)
{
totalFit += ants[i].GetFoodCollected;
}
return totalFit;
}
And the output:

Here, the green dots represent the food, the green number with each ant is the number of food collected, the yellow number is the ant number, and the list on the right shows the details of the previous generations.
Do the experiment with turning the "Land Mines" on.
References
- Steering Behaviors For Autonomous Characters
- Programming Game AI by Example - Mat Buckland
- Al Application Programming - M. Tim Jones
- Neural Network Design - Martin T. Hagan
- Genetic Algorithms
History
- 26/08/2008: Initial release
- 09/10/2008: Minor changes & code improvement
