FuzzyAdvisor - A Simple Fuzzy Logic Expert System in F#

• Download source - 108 KB

Introduction

Some 15 or more years ago, I was involved in a project (Brulé, et. al., 1995) that needed an expert system to choose a suitable option based on some basic parameters. Several approaches were tried, including the use of predicate calculus (i.e., Prolog). Essentially, none of the approaches worked very well. Finally, I interviewed several human experts in the subject. I would ask what choice they would make given a set of parameters, and they invariably would answer with something like "If X is Y, then I would use A, but if X is Z, then I'd use B" -- where X is a parameter (i.e., water depth), Y and Z are qualifiers (deep), and A and B are options that can be chosen. A little reflection, and it suddenly became apparent that they were describing a fuzzy system. As a result, I ended up coding a simple fuzzy logic based expert system, and solved the problem satisfactorily.

More recently, I decided to dive into F#. As a novice in functional programming, I thought that some of the features of F# might be a good match for a simple expert system, similar to what I developed in the last century. My initial observations on F# and writing a Windows Forms application are in a previous article, Getting Started in F# - A Windows Forms Application[^].

In this article, I'll present FuzzyAdvisor, a simple fuzzy logic based expert system useful for making choices based on simple parameter estimates. The download contains three Visual Studio 2008 projects:

• FuzzyAdvisor - the core library (*.dll) written in F# that implements the advisor system.
• FuzzyWorkshop - an F# application allowing specifying rules, visualizing fuzzy sets, and testing the FuzzyAdvisor system.
• FuzzyTest - a C# project that uses FuzzyAdvisor as an example of combining languages.

Of course, I'll add my usual disclaimer: I'm still a beginner at F#, so I don't make any claims that the code is elegant, efficient, etc. It does work and, as always, any comments on the coding style or alternate F# techniques will be appreciated.

Description of the FuzzyAdvisor System

In the oil business, as well as other industries, it is often necessary to make preliminary estimates of costs before there is a lot of data available. In the development of offshore oil fields, the cost of an offshore platform or other type of facilities design has extremely important implications on costs, lead time before installation, drilling constraints, environmental risks, etc. Due to these concerns, it is very important that a reasonable choice of facility is selected at the outset of a project, long before any other meaningful data is available. The example discussed here will use some rudimentary data to make an educated guess at the best type or types of offshore oil facilities. It should be noted that the early version of this Fuzzy Advisor system was successfully used in many other similar decision processes, including the selection of gas compressors, pumps, and refinery equipment.

You can also be assured that I do not know the exact rules that should be used, so the information presented here is contrived, but reasonable. In other words, don't think you can apply these rules to making real world decisions! You'll need to figure out your own rules, or hire an expert to help with that.

The overall design of FuzzyAdvisor is to process fuzzy rules of the form:

if <parameter> is <quantifier> then <option> <weight>

For example:

if Water Depth is VeryDeep then SubseaCompletions (0.9)

In the example, notice that Water Depth represents a data parameter, VeryDeep describes a fuzzy set, SubseaCompletions is an option that might be selected, and 0.9 is a weighting factor that describes how important the rule is.

Notice also that the statement can be easily read in plain English, even by experts who know nothing about fuzzy logic or programming, yet it can be translated to fuzzy logic operations in a very straightforward manner. This form of statement grammar is extremely important, since the subject experts can easily read the rules and decide whether or not they make sense. Such considerations are often of paramount importance in gaining acceptance of the system and ensuring that the subject experts are not alienated in the decision making process.

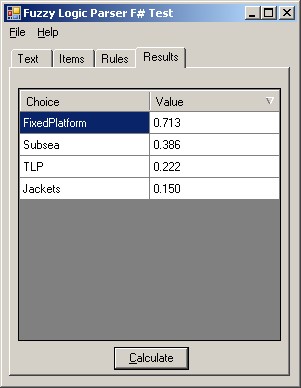
The entire system then consists of a list of rules, a list of parameter values, a list of fuzzy sets, and a list of choices. Once the parameters have been specified, the membership in each fuzzy set is evaluated, and the adjusted weight is added to the choice specified in each rule. When all of the rules have been evaluated, the choices are sorted in decreasing order of their value and presented to the user for consideration.

It is also important to note that in the "real world", there quite often is no "right answer", because everything involves tradeoffs in terms of time, resources, cost, and other considerations. FuzzyAdvisor recognizes this by ranking the options and letting the user choose the best one based on any other subjective information they might have. On the other hand, FuzzyAdvisor, with a properly defined set of options and sufficiently well calibrated rules, will indicate any options that are either totally impractical or head and shoulders above other choices.

In implementing a FuzzyAdvisor system, it is necessary to define the rules, determine the fuzzy sets, and specify the weighting factors for each rule. Although I won't go into the details of that process, the preliminary definitions are normally determined by interviewing subject matter experts. Once the preliminary rules, fuzzy sets, and weights are determined, the system is implemented and reviewed once again by the experts. When they note a bad decision, it is then necessary to figure out whether to adjust a fuzzy set or a weight, or perhaps add a different rule. Actually, doing that is beyond the scope of this article.

FuzzyAdvisor Grammar

The FuzzyAdvisor system reads parameters, fuzzy set definitions, and fuzzy rules in plain text format using a very simple grammar. There are three types of statements in the grammar:

• Parameters: VAR <varname> of <context> = <value>
• Fuzzy Sets: FSET <fsetname> of <context> <membership list>
• Fuzzy Rules: IF <varname> of <context> IS <fsetname> THEN <option> <weight>

Note that the context of a parameter and a fuzzy set must match in order to distinguish between parameters with similar or identical names, but different meanings; for example, Depth of Water, as opposed to Depth of a Well. In addition, for convenience, any of the <name> of <context> constructs can be replaced with <context> <name> for flexibility. In other words, we can equivalently write Depth of Water or Water Depth.

The FuzzyAdvisor is implemented in F# using four types. The complete code is in the project files, but I'll mention some of the interesting points.

First, since the various types (classes in C#) reference each other, in F#, they must be defined together. The first type is preceded by the type keyword, but the following ones use the and keyword instead, as shown in the following code snippet:

type FuzzyVariable(VName : string, VContext : string, VValue : float) =
    let name = VName
    let context = VContext
    let mutable value = VValue
    new(vn, vc) = new FuzzyVariable(vn, vc, Double.NaN)
    override this.ToString() = sprintf "%s.%s" name context
    member this.Name = name
    member this.Context = context
    member this.Value
        with get() = value
        and  set v = value <- v

and FuzzySet(FName : string, FContext : string, FValues : (float * float) list) = 
    let name = FName            // Fuzzy set name       i.e. hot
    let context = FContext      // Fuzzy set context    i.e. water temperature
    let values = FValues        // list of (value, membership) tuples in 
                 // increasing order of value
    new(fn, fc) = new FuzzySet(fn, fc, [])
    override this.ToString() = sprintf "%s.%s" name context
    member this.Name = name
    member this.Context = context
     ...
        
and FuzzyRule(AVar : FuzzyVariable, AFSet : FuzzySet, 
            AChoice : string, AWeight : float) =
    let variable = AVar
    let fuzzySet = AFSet
    let choice = AChoice
    let weight = AWeight
    override this.ToString() = sprintf "%s (%A): %s is %s" 
        choice weight (variable.ToString()) (fuzzySet.Name)
    member this.Var
        with get() = variable;
    member this.FSet
        with get() = fuzzySet;
    member this.Choice
        with get() = choice;
    member this.Weight
        with get() = weight;

and FuzzyAdvisorEngine() =
    let mutable fuzzySets:(FuzzySet list) = []
    let mutable fuzzyVars:(FuzzyVariable list) = []
    let mutable fuzzyChoices:((string * float) list) = []
    let mutable fuzzyRules:(FuzzyRule list) = []
     ...

Note also that I've overridden the normal ToString() method for each of the objects. This allows me to add the objects to a list box and have meaningful names displayed.

To perform the text parsing, I chose to use a brute force method, due to the simplicity of the grammar. In F#, this is easily accomplished with list processing and pattern matching. The following snippet shows part of the parser. Note that a line is split into a list of words separated by spaces, then pattern matching is used to determine what type of statement it represents based on the first word. Finally, pattern matching is again used to extract the various <name><context> items and any associated values. The FuzzyAdvisorEngine contains functions to read and parse text from either strings or a text file. During the parsing, lists of variables, Fuzzy sets, and Fuzzy rules are accumulated. Valid options are also determined from the rules and saved in a list of choices.

let Parse1Line(lineRead, iLine) =
    let line = if lineRead <> null then String.split [' '] lineRead else []
    match line with
    // Ignore comment and blank lines
    | "//"::_ -> null
    | [] -> null

    // Parse Variables
    | x::words when x.ToUpper() = "VAR" ->
        match words with
        | name::"of"::context::"="::value::_ when Double.TryParse(value) |> fst ->
            let var = new FuzzyVariable(name, context, Double.Parse value)
            fuzzyVars <- var :: fuzzyVars
        | context::name::"="::value::_ when Double.TryParse(value) |> fst ->
            let var = new FuzzyVariable(name, context, Double.Parse value)
            fuzzyVars <- var :: fuzzyVars
        | _ -> failwith ("Invalid VAR on line "^(iLine.ToString()))

    // Parse FuzzySet definitions
    | x::words when x.ToUpper() = "FSET" ->
        match words with
        | name::context::(values:(string list)) ->
            let comparePoints (x1,_) (x2,_) = compare x1 x2
            let getPoint (s:(string list)) =
                match s with
                | x:string::y:string::[]
                    when (Double.TryParse(x) |> fst) &&
                (Double.TryParse(y) |> fst) ->
                        (Double.Parse x, Double.Parse y)
                | _ -> failwith ("Invalid FuzzySet Value on line "
                        ^(iLine.ToString()))
            let rec getValues (s:(string list)) =
                match s with
                | [] -> []
                | x::y -> getPoint (String.split['(';',';')'] x) :: getValues y
            let fset = new FuzzySet(name, context, (getValues values) |>
                    List.sort comparePoints)
            fuzzySets <- fset::fuzzySets
        | _ -> failwith ("Invalid FSET on line "^(iLine.ToString()))

    // Parse FuzzyRules
    | x::words when x.ToUpper() = "IF" ->
        let rule =
            match words with
            | name::"of"::context::"is"::fsname::choice::value::_
                when Double.TryParse(value) |> fst ->
                let var = getVariable(fuzzyVars, name, context)
                let fset = getFuzzySet(fuzzySets, fsname, context)
                new FuzzyRule(var, fset, choice, Double.Parse value)
            | context::name::"is"::fsname::choice::value::_
            when Double.TryParse(value) |> fst ->
                let var = getVariable(fuzzyVars, name, context)
                let fset = getFuzzySet(fuzzySets, fsname, context)
                new FuzzyRule(var, fset, choice, Double.Parse value)
            | _ -> failwith ("Invalid RULE on line "^(iLine.ToString()))
        fuzzyRules <- rule :: fuzzyRules
        if List.exists (fun (z,_) -> z = rule.Choice) fuzzyChoices then
            null
        else fuzzyChoices <- (rule.Choice, 0.0) :: fuzzyChoices
        |> ignore

    // If none of those match, it must be an error
    | _ -> failwith ("Invalid line "^(iLine.ToString())^"= "^lineRead)

FuzzyWorkshop

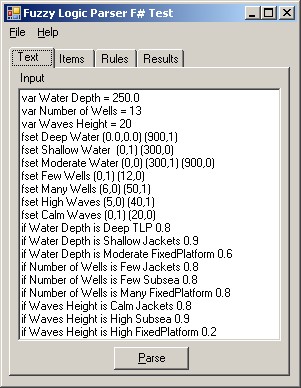
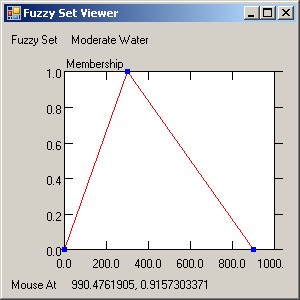
The FuzzyWorkshop application is a Windows Forms application written completely in F# that allows testing the FuzzyAdvisor system. The TabControl on the main form contains pages for text, items (Fuzzy sets and parameters), rules, and results. Text can be saved to and read from a text file using the menu options. Pressing the Parse button will attempt to parse the text and determine the Fuzzy sets, variables, Fuzzy rules and choices. Once parsed, double clicking on a Fuzzy set will display a graph of the set membership to help in troubleshooting. On the Results tab, pressing the Calculate button will process the rules and show the weighted ranks of all the possible choices.

Most of the FuzzyWorkshop code is straightforward, but there are several interesting parts. First, the TabControl is added to the main form as follows, with the required buttons, list boxes, etc., added as controls on the individual TabPages. As I mentioned in the previous article, all of this must be done manually, since there are no form designers available for F# (yet?).

let tabControl = new TabControl()
let tab1 = new TabPage()
let tab2 = new TabPage()
let tab3 = new TabPage()
let tab4 = new TabPage()
...
    // tabControl
    tabControl.Location <- new Point(5, 5)
    tabControl.Height <- 260
    tabControl.Width <- 280
    tabControl.Anchor <- AnchorStyles.Top |||
      AnchorStyles.Left ||| AnchorStyles.Right |||
      AnchorStyles.Bottom
    tabControl.TabPages.Add(tab1)
    tab1.Text <- "Text"
    tabControl.TabPages.Add(tab2)
    tab2.Text <- "Items"
    tabControl.TabPages.Add(tab3)
    tab3.Text <- "Rules"
    tabControl.TabPages.Add(tab4)
    tab4.Text <- "Results"
    tab1.Controls.AddRange([|
                            (btnParse:> Control);
                            (label1:> Control);
                            (txtInput:> Control);
                           |])
    tab2.Controls.AddRange([|
                            (label2:> Control);
                            (lstFuzzySets:> Control);
                            (label3:> Control);
                            (lstVariables:> Control);
                           |])
    tab3.Controls.AddRange([|
                            (label4:> Control);
                            (lstRules:> Control);
                            (btnCalculate:> Control)
                           |])
    tab4.Controls.AddRange([|
                            (btnCalculate:> Control);
                            (grid:> Control)
                           |])
...

In addition, the FuzzyGraph is implemented as a user control. The details are in the source files, but basically a FSharpGraph type is defined that inherits from a .NET UserControl. Members are defined to react to mouse movements, to add data to the graph, etc. All of the graphics is programmed using basic GDI methods. Once defined, the FSharpGraph component is added to a regular form, which is loaded on the MouseDoubleClick event for the FuzzySet listbox. Portions of the applicable code are shown below:

type FSharpGraph() as graph =
    inherit UserControl()
    let mutable components = new System.ComponentModel.Container()
    // Mouse control
    let mutable mouseSelecting = false
    let mutable mouseX1 = 0
    let mutable mouseY1 = 0
    let mutable mouseX2 = 0
    let mutable mouseY2 = 0
    let mutable graphMouseMove:(float -> float -> unit) = fun _ _ -> null
    ...

type FuzzySetViewerForm(fset : FuzzySet) as form =
    inherit Form()
    let label1 = new Label()
    let lblName = new Label()
    let label2 = new Label()
    let lblMousePosition = new Label()
    let graph = new FSharpGraph()
    let mutable FSet = fset
    do form.InitializeForm

    // member definitions
    member this.InitializeForm =
        // Set Form attributes
        this.FormBorderStyle <- FormBorderStyle.Sizable
        this.Text <- "Fuzzy Set Viewer"
        this.Width <- 300
        this.Height <- 300
        ...
        // graph
        graph.Location <- new Point(10,30)
        graph.Size <- new Size(270,220)
        graph.Anchor <-  AnchorStyles.Top ||| 
    AnchorStyles.Left ||| AnchorStyles.Right ||| AnchorStyles.Bottom
        graph.GraphMouseMove <- (fun x y -> this.GraphMouseMove(x, y))

Note that the last line of code above assigns a function to the GraphMouseMove member in order to trap the mouse location parameters and display them on the form. This is similar to the use of a delegate in C#.

Additionally, the following code is used to populate the list boxes and other displays after parsing a text file. To me, it's amazing what can be done with a single line of code and F#'s internal list processing functions, such as List.iter and List.rev. Note that the lists are reversed using List.rev only so that the displays show up in the same order as the text file declarations. Using the lstVariables line as an example, the F# code basically says to iterate over a list of variables, adding each one to the listbox and discarding the result (an integer). The list to iterate over is fuzzyEngine.FVars after it has been reversed using (List.rev fuzzyEngine.FVars).

let AddChoice (n,s) =
    let row = grid.Rows.Item(grid.Rows.Add())
    row.Cells.Item(0).Value <- n
    row.Cells.Item(1).Value <- s.ToString()
List.iter (fun x -> lstVariables.Items.Add(x) |> ignore) 
        (List.rev fuzzyEngine.FVars)
List.iter (fun x -> lstFuzzySets.Items.Add(x) |> ignore) 
        (List.rev fuzzyEngine.FSets)
List.iter (fun x -> lstRules.Items.Add(x) |> ignore) 
        (List.rev fuzzyEngine.FRules)
List.iter (fun x -> AddChoice(x) |> ignore) (List.rev fuzzyEngine.FChoices)

FuzzyTest

The FuzzyTest application is a simple Windows Forms application written in C# that accesses the FuzzyAdvisor written in F#. The C# source code used to access the FuzzyAdvisor system is shown below. Note that the FuzzyAdvisorEngine is created, a text file is selected using a standard .NET FileOpen dialog, and the engine reads and parses the file and then calculates the choices. In the sample, the ranked choices are simply shown using a MessageBox, but of course, they could be presented in an alternate form, or program actions could be determined based on the rankings. Note that the F# tuples used to define choices are accessed from C# using the Microsoft.FSharp.Core.Tuple<string,> generic class.

FuzzyAdvisor.FuzzyAdvisorEngine Engine = null;

...

private void button1_Click(object sender, EventArgs e)
{
    if (dlgFileOpen.ShowDialog() == DialogResult.OK)
    {
        Engine = new FuzzyAdvisor.FuzzyAdvisorEngine();

        Engine.LoadFromFile(dlgFileOpen.FileName);
        Engine.get_CalculateChoices();
        foreach (Microsoft.FSharp.Core.Tuple<string, /> t in Engine.FChoices)
        {
            MessageBox.Show(t.Item1 + " = " + t.Item2.ToString());
        }
    }
}

To create the FuzzyTest project, a C# project was first created, then an existing project was added to the solution. Choosing the FuzzyAdvisor project adds it to the solution easily enough. It is also necessary to add the F# references FSharp.Core and FuzzyAdvisor to the C# project, since Visual Studio will not automatically recognize those that are required. Once the projects are created, they can be built and tested normally, and debugging can even step through both the C# and the F# code.

Conclusions

While the FuzzyAdvisor system presented here is fairly simple, it provides an example of a complete F# program, and shows how classes written in F# can be used in C# or other .NET languages. The system can be extended to incorporate more complex fuzzy logic, include hedges, and allow ranges of results when some of the variables are not precisely known. In addition, rather than simply presenting the choices, it would be fairly straightforward to apply an additional defuzzification step and then use the results to automatically perform other actions. Such techniques have been tested and found to work for some automated control systems, but have not been implemented in this example.

After learning to use F# and figuring out how to make components, forms, libraries, and how to use F# code along with C#, it seems to me that the optimum use of F# for the short term is to handle processes which mainly involve non-graphical and non-user input. Partly due to the availability of the form designers, other languages such as C# seem much better for user interfaces.

On the other hand, the ability to simply do recursive programming, define generic first-class functions, and process lists makes F# ideal for some tasks. In particular, once we get used to the syntax, things which are somewhat complex iterations in other languages suddenly become elegant one liners in F#.

Finally, I still recommend that anyone with even the slightest curiosity spend some time and learn how to use F#. It never hurts to be able to add another tool to one's programming toolbox, nor is it a disadvantage to be able to look at a problem from a different viewpoint. Personally, I'm sure I'll find uses for F# in the future, combining it with other programming languages.

References

• Brulé, Mike, Walt Fair, Jr., Jun Jiang, Ron Sanvido, A RAD Approach to Client/Server System Development, SPE Computer Applications, Society of Petroleum Engineers, October 1995, p122ff.

History

• 8 November, 2008 - Initial submission.