<pre />
Introduction
One of the most common problems is to compute an answer to
an equation. If it is a simple equation with one unknown variable and the
variable can be isolated it’s easy to solve, such as computing y:
y = a*x +b, y = a0 + a1*x + a2*x^2, y = a0*e^x, y = x^(a/x + b)
The problem is much harder when solving for a, b based on
measured x, y values. Common examples include solving for the location of a GPS
receiver from a set of measurements, curve fitting an NMR return to a Lorentz
distribution, computing the apparent time constants of a heat system from
recorded data, or computing the solution to a transcendental function.
The classical technique to solve numerically is to compute an
error function, and search (guess) for a solution that minimizes the error.
Different problems lend to different approaches. But it is often through an
iterative process.
This article describes some classical approaches, and
presents a novel approach blending the
advantages of some of the techniques presented that is often useful. Often the “optimal” technique depends on how
much computing power and time is available, the accuracy required, and the
smoothness and shape of the error function. Finding an optimal technique is in
part subjective and relative to the problem, and it is an art. The provided new
approach is meant to provide an interesting example.
The source code provided, and it is relatively simple to
use, the caller defines an error function (delegate/callback) and an initial
estimate of the function’s coefficients.
As an API, a large number of problems can be solved with a few calls
without understanding the mathematics behind it.
Background
These are very flexible techniques. The solution converges
quickly if you can describe what you do want (or not) as an error function to
minimize, preferably with a smooth monotonic slope.
Example 1
Suppose you have a set of data points, and you need to
calculate the line that “best” fits that line.
y = mx + b
In this case, y and x are known, but given any two pairs of
y and x, a different pair of m and b are calculated due to measurement noise.
The goal is to minimize the error of the points.
The error function could be, given a “b” and an “m”, compute
a predicted y for each known x, then:
Error =
sum( (y-ypred)*(y-ypred)) for all y
and ypredicted.
This is
a simple problem to solve with least squares, the provided source code
demonstrates how to fit a line or a quadratic to a data set. Both a linear and
quadratic solver (Solve_FirstOrder, Solve_SecondOrder) calls are provided. Note
this minimizes the square of the error and not the delta error which is often
more desirable if there is noise in the x, y measurements.
LinearLeastSquares lls = new LinearLeastSquares();
double [] x = {1, 2, 3, 4, 5};
double [] y = {3, 5, 7, 9, 11};
lls.Solve_FirstOrder(x, y);
if ((1 = lls.Solution[0])&& (2 == lls.Solution[1]))
{
}
Example 2
Computing where you are from several noisy distance
measurements or angle measurements from known points (GPS / triangulation). In
this case if you were where your guess (coefficients) said you were, then the
actual measurements would have a certain value, and the difference between
predicted and actual is the error. In this case, the error transformed by
derivative of value vs parameter translates the error into an update to the
estimate. This is the basis of what is called non-linear least squares, or the
Gauss-Newton method. In its simplest form:
J*dA = R
dA is adjustment to
coefficients as a vector,
R is error at each x position as a vector.
J is a matrix called the Jacobian, the coordinate transform
from error to coefficient
1. A = initial estimate
2. dA = J^-1 * R
3. A = A + dA
4. Stop if magnitude of R is small enough, else go to step
2.
The matrix grows in both number of
measurements and coefficients, and often it isn’t square, and when squared up
multiplying by the transpose of J, it sometimes isn’t invertible. In these
cases, a pseudo inverse is used. The problem with the pseudo inverse is it
sometimes isn’t accurate due to round off problems, different matrix packages
use different approaches to minimize the problem. Sometimes this method doesn’t
converge to a solution without modifying it.
For these reasons, an iterative non-linear
code example isn’t provided, it would be too large and complex, and in general,
a creative solution guessing scheme converges faster.
Example 3
Suppose heat is transferred from A to B, and B to C. We
might now the heater current applied at A, and the temperature at C, but
nothing directly about how heat was transferred through B.
B =
(B-A)*e^(-t/tba) - (C-B)*e^(-t/tbc)
You have the values of C and A, but not B, nor
the time constants tba and tbc, and exponential functions are far from linear.
If there is a unique solution that minimize the error (what we measured minus
what the guessed at constants would predict) then the problem can be solved
for. In this case the non-linear least squares would also work but as more
coefficients are added, that solution might converge to different local
minimums given different initial estimates and not converge to the ideal
answer.
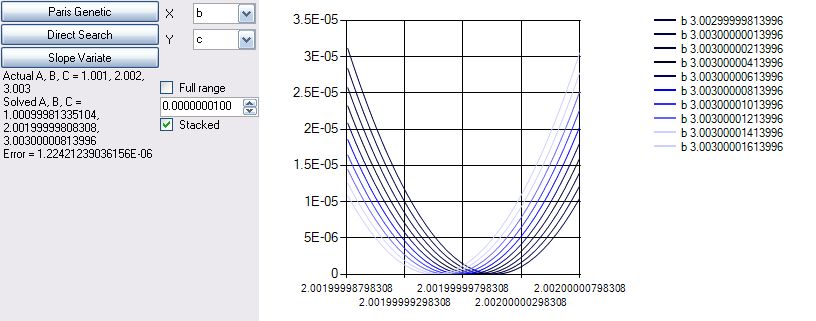
double a = 1.001, b = 2.002, c = 3.003;
for (int i = 0; i < data.Length; i++)
{
double di = (double)(i * 0.1);
data[i] = a*di*di + b*di*System.Math.Exp(di) + c*System.Math.Exp(di + 1);
}
Solver.Parameter pa = new Solver.Parameter(
"a",
1.05,
1.2,
0.8,
0.1,
0.0001);
Solver.Parameter pb = new Solver.Parameter("b", 2.05, 2.1, 1.9, 0.1, 0.0001);
Solver.Parameter pc = new Solver.Parameter("c", 3.05, 3.1, 2.9, 0.01, 0.0001);
s.Parameters.Add(pa);
s.Parameters.Add(pb);
s.Parameters.Add(pc);
Solver s = new Solver();
s.Solve_DirectSearch(ComputeError, 10, 10, 1.25, 0.00005);
pa.CenterValue = pa.Solution;
pb.CenterValue = pb.Solution;
pc.CenterValue = pc.Solution;
double err = s.Solve_SlopeVariate(ComputeError, 20, 5, 1.25, 0.00000000005);
err = System.Math.Sqrt(err) / data.Length;
label1.Text =
"Actual A, B, C = " + a + ", " + b + ", " + c + "\r\n" +
"Solved A, B, C = " + pa.Solution + ", " + pb.Solution + ", " + pc.Solution +
"\r\nError = " + err;
Theory
Most approaches used by the author or seen in documentation
require an error function, and then guess, improve the guess and repeat, a
rough sketch of this is:
- Initial guess
- Compute error
- Refine guess
- Compute error
- If error isn’t small enough, go to step 3, else repeat.
What varies per algorithm is how the refine step is done:
Genetic:
Create
a set of possible coefficients, repeat with a single “best” or a few “best”
values.
Direct Search:
Vary
one parameter at a time, repeat while reducing the step size.
Least Squares:
Treat the error as a translatable vector space
from the solution.
Slope Variation:
Curve fit (least squares) the effect of one
coefficient on another, direct search in pairs.
Key Feature Comparison
Plotting the error vs. any two coefficients produces a
surface plot. Picture trying to find the lowest spot on a map, but only knowing
the altitudes of the places visited.
·
Least Squares flattens the errors into a
solution, but if the map is too complex that won’t work.
·
Iterative least squares uses the slope to get
magnitude and direction of where to try next, but if the second derivative (rate
of change of slope, or Hessian) or higher order things are at play, then the
direction and or magnitude may lead to a relatively equivalent error in a new
location, the solution might not converge. Inverting
large matrixes is time consuming.
·
Using higher order derivatives (Hessian matrix)
can help if the curve is very smooth (no noise), and there are few divots in
the surface (local minima) the algorithm might lock onto.
·
Checking a geometric pattern to compute a search
region (simplex method) or a grid pattern, and then refining the search region
iteratively (genetic) around likely candidates works well if there is noise and
local minima, but it takes of computations. For 5 coefficients, a single 20
test point search is 20^5 = 3,200,000 error calculations. If each error
calculation computes the sum of the errors for 10k data points, and 20
iterations, this may be 640 billion calculations. Solving the same problem at
10 Hz would likely require over a 20 GHz processor.
·
Varying only one parameter at a time is called a
pattern search or direct search, or Hook-Jeeves algorithm. In this case the
solution is explored starting at one location walking in one strait line at a
time, varying step size. In general, setup appropriately, Hook-Jeeves overshoots/undershoots
and explores to find the solution. The disadvantages is it may lock onto a
local minimum, or it may jump over a local minimum. With a large number of
coefficients, varying each in order can also tend to jump across local minima.
Testing for 5 coefficients with 10k data points may take 1000 iterations or 50
million calculations instead of 640 billion. At
10Hz, this might be done with a dual core processor, GPU or an ASIC.
Theory of the new algorithm
There are many cases why an algorithm may fail to converge
on the correct solution. Suppose, that the error map of two coefficients has a
narrow deep trench, at some angle to the coefficient axis. That is usually the
reason why other methods that are good at initially converging on the right
solution stop converging. In this case, most searches will not lock onto the
trench, and follow it and instead lock onto some cross section across it, and
reduce step size without converging on the correct solution. Noise, and local
minima will make matters worse.
This is an error plot of two coefficients in a complex
equation (lighter is less error, ideal solution in center).


The error has a dominant
trench from left to right that most algorithms will lock onto, some will lock
into the center trench, but most will not be able to converge within it very
well. The solution optimized within the center diagonal well would require the
algorithm to detect, vary and trace along that point.
There are several approaches that “rotate” to the trench
using Hessian or slopes but they are susceptible to noise, and work best when
the trench isn’t curved, and there are not ripples in the surface.
For two coefficients a, and b, a slice through the map at a
given b, sampled a few times at a step size provides a line. When that line can
be approximated by a least squares curve, and that curve has a bottom, then
that bottom point is the bottom of the trench in that slice. Linking the
“bottom” points of multiple slices and then least squares fitting again
provides the line that is the bottom of the trench for coefficients a and b.
Due to noise, etc. when the step size is large enough it will skip over local
minima and other ripples in the error surface that are small. The algorithm
will also track a curved trench. As the step size is reduced the algorithm will
continue to converge.
To ensure the refinement is real, and not due to noise the
refinement is done as a pair, and only applied if the same refinement can be
made when starting with “a” OR by starting with “b”.
The algorithm has several nice properties:
- ·
Axises are chosen in pairs (every combination),
so if any combination could be improved the algorithm rapidly converges.
- ·
Subsampling at an interval that reduces locks
onto major features of the error function and tends to ignore local minima.
- ·
When the algorithm does lock onto a local
minima, the affect of refining another pair of axis will generally “pop” the
system out of that minimum.
- ·
Algorithm converges extremely quickly.
- ·
Uses least squares to fit a quadratic and
assumes another algorithm has provided a relatively good initial estimate.
The algorithm has one significant weaknesses but can be
covered by combining it with a another algorithm. If there isn’t a dominant
minimum within the range of values being examined the algorithm doesn’t work.
When first providing likely “estimate” locations via a genetic grid search this
isn’t a problem.
Performance
Performance is relative to the equation chosen. There are
large sets of equations that are best suited for each algorithm, the following
demonstrates a typical case where the “Slope Variation” approach works better
than others.
y = (1.001)*x^2 + (2.002)*x*e^x + (3.003)*e^(x + 1)
Paris Genetic 0.9, 2, 3.00999 Error 0.4099, 10k error function evaluations.
Paris Genetic
Multiple 0.9, 2, 3.00999 Error
0.4099, 40k error function evaluations.
Direct Search 1.13, 2.00259, 3.00055, Error of 0.2157, 2k
error function evaluations
Slope Variation 0.96177, 2.00163, 3.00439, Error of 0.047, 200 error function evaluations.
Slope Variation 1.000994, 2.0019999, 3.00300, Error of 6.35
x10^-6, 19.7k error function
evaluations.
The Paris and
Direct search techniques, could only marginally improve the error over time and
converged slowly if at all towards the end. The Slope Variation method
converged rapidly, and continues to converge rapidly, where other techniques do
not.
Conclusion
When paired with an initial method to produce a refined
estimate, the new method will often converge far more quickly and continue to
converge almost to an arbitrary level of precision. These features make it a
good approach to refine a likely solution quickly.
References
The zip file includes a pdf with a lot of the math done out by hand for some of the methods. Most use the same coefficient names or similar to what is shown in wikipedia to avoid confusion.
http://en.wikipedia.org/wiki/Non-linear_least_squares
http://en.wikipedia.org/wiki/Genetic_algorithm
http://en.wikipedia.org/wiki/Pattern_search_%28optimization%29
