Introduction
I was learning an AI course in my college and learned about Constraint Satisfaction Problems (CSP). The lecturer asked for little solver projects, and I thought... Sudoku! Here's a classic CSP.
Sudoku?
I guess everyone knows Sudoku; for those who don't, try Google or Wikipidia.
The basic rule(s) of Sudoku are:
- For each row/column/region, you have to use distinct numbers.
- All cells have to be assigned.
A Sudoku board is a NxN matrix, which means we need to use a number in the range [1..N].
What is a CSP?
A CSP or a Constraint Satisfaction Problem is defined by three items:
- a finite set of variables.
- a function that maps each variable to a finite domain.
- a finite set of constraints.
Constraint propagating and backtracking search are some techniques in CSP, and these are the two ideas I will be describing in this article.
Setting up the problem (Or, what that has to do with Sudoku?)
Before we start, I want to list some definitions:
- Cell: A cell is a 'square' in a Sudoku grid.
- Grid: A grid represents the Sudoku board.
- Peers: All the cell's neighbors; neighbors are cells that are in the same unit of the cell.
- Unit: A collection of
GRIDSIZE cells, for each row, column, and region. - Region: A region is a small square, mostly sqrt(N) x sqrt(N) sized.
The algorithm here will be described using two methods based on CSP ideas: constraint propagation and backtracking search.
First, we need to define the Sudoku problem as a CSP.
- Variables: The variables will be each cell on the grid.
- Domain: The domain will be any digit from 1 to
GRIDSIZE. If GRIDSIZE >9, I will use letters from 'A' to.. however much I need, where 'A' equals to 10 , 'B' to 11, and so on. - Constraints: The constraints are:
- Same digit (or letter) can't appear twice (or more) in the same row.
- Same digit (or letter) can't appear twice (or more) in the same column.
- Same digit (or letter) can't appaer twice (or more) in the same region.
I implemented the domain of variables as strings (for efficiency), and when any cell domain length becomes 1, we will have a solution!
Constraint propagation
Of course, I could just do some bruteforce, check options, and find a solution (it might take time, but it works), but can I do it better? Yes, I can.
A key issue in CSP is constraint propagation; we will see two types: Forward checking and ARC consistency.
Forward Checking
The most elementary constraint propagation is forward checking. It means eliminating, in advance, the possibilities that do not match the constraints from the domains of unassigned variables. For example, if we assign the digit 'd' to cell c1, we eliminate 'd' from all the domains of this cell's peers.
MyCell[,] EliminateFC(MyCell[,] branch, Pos p, char val)
{
branch[p.ln, p.col].Value =
branch[p.ln, p.col].Value.Replace(val.ToString(), "");
return branch;
}
MyCell[,] AssignFC(MyCell[,] branch, Pos p, char val)
{
for (int i = 0; i < branch[p.ln, p.col].Peers.Count; i++)
{
branch[branch[p.ln, p.col].Peers[i].ln, branch[p.ln, p.col].Peers[i].col].Value =
branch[branch[p.ln, p.col].Peers[i].ln,
branch[p.ln, p.col].Peers[i].col].Value.Replace(val.ToString(), "");
if (branch[branch[p.ln, p.col].Peers[i].ln,
branch[p.ln, p.col].Peers[i].col].Value.Length == 0)
return null;
}
branch[p.ln, p.col].Value = val.ToString();
branch[p.ln, p.col].assigned = true;
return branch;
}
Arc consistency
What I do is not exactly arc consistency, but is based on that. I'm doing three types of diminutions, some for reducing domains and some just to see a mistake in advance for saving time:
- When we want to assign the digit 'd' to cell s1, we use assign(cells, s, d). By doing that, I want to assign to s the value d (daa..), but I also want to eliminate this possibility from its peers (like FC does, tell me something new!). If the elimination causes one (or some) of the peers going down to only one possibility, which we call d2, we want to assign d2 to it, and by doing that, eliminate d2 from all of its peer's peers, and that could make another chain reaction. This chain reaction is simply called constraint propagation: placing a constraint on one cell can cause further constraints to be placed on other cells.
- The second type: let's say we just eliminate 6 as a possible value of cell [0,0], and we would look on the first unit (the rows unit) of [0,0] and see that the only cell who has 6 as a possibility is [0,7]. We will assign 6 to [0,7], and again, a chain reaction happens.
- The last one is a pre-check for mistakes, because Sudoku is declared as an AllDiff constraint. We can check in advance for a valid solution by doing the following simple form of inconsistency detection: if there are M variables involved in the constraint and if they have N possible distinct values altogether, and M>N, then the constraint cannot be satisfied (and we don't have to spend time on this branch that will eventually go wrong.)
MyCell[,] AssignWithAc3(MyCell[,] Cells, Pos assignmentPosition, char assignmentValue)
{
for (int i = 0; i < m_gridSize; i++)
if (m_MaxDomain[i] != assignmentValue)
{
Cells = EliminateWithAc3(Cells, assignmentPosition, m_MaxDomain[i]);
if (Cells == null)
return null;
}
Cells[assignmentPosition.ln, assignmentPosition.col].assigned = true;
return Cells;
}
MyCell[,] EliminateWithAc3(MyCell[,] Cells,
Pos assignmentPosition, char assignmentValue)
{
if (!Cells[assignmentPosition.ln, assignmentPosition.col].Value.Contains(
assignmentValue.ToString()))
return Cells;
Cells[assignmentPosition.ln, assignmentPosition.col].Value =
Cells[assignmentPosition.ln, assignmentPosition.col].Value.Replace(
assignmentValue.ToString(), "");
if (Cells[assignmentPosition.ln, assignmentPosition.col].Value.Length == 0)
return null;
if (Cells[assignmentPosition.ln, assignmentPosition.col].Value.Length == 1)
{
Cells[assignmentPosition.ln, assignmentPosition.col].assigned = true;
char val2 = Cells[assignmentPosition.ln, assignmentPosition.col].Value[0];
for (int i = 0; i < Cells[assignmentPosition.ln,
assignmentPosition.col].Peers.Count; i++)
{
Cells = EliminateWithAc3(Cells, Cells[assignmentPosition.ln,
assignmentPosition.col].Peers[i], val2);
if (Cells == null)
return null;
}
}
for (int i = 0; i < 3; i++)
{
int n = m_gridSize;
int m = 0;
List<Pos> val_place = new List<Pos>();
for (int j = 0; j < Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i].Count; j++)
{
if (Cells[Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].ln,
Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].col].assigned)
n--;
else
m++;
if (Cells[Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].ln,
Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].col].Value.Contains(
assignmentValue.ToString()))
{
val_place.Add(new Pos(Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].ln,
Cells[assignmentPosition.ln,
assignmentPosition.col].Units[i][j].col));
}
}
if (m > n)
return null;
if (val_place.Count == 0)
return null;
if (val_place.Count == 1)
{
Cells = AssignWithAc3(Cells, val_place[0], assignmentValue);
if (Cells == null)
return null;
}
}
return Cells;
}
OK, this was the first step, but some Sudoku doesn't leave us any choice and force us to do some guessing to find the solution. But, what if we guess wrong? We have to backtrack, therefore we have the backtracking search, simple? It is getting clever, you'll see.
Backtracking search
By using the backtracking search, we can move through the tree and check any possibility (but if we are smart, we don't need to) for inefficiencies. But, because of the constraints, every bench becomes smaller and smaller, and if we use some heuristics, we can do a lot better!
The backtracking search goes like this: if we already have a valid solution, return the solution; if we do not, we choose a unfilled cell (which cell? we'll see..!) and consider all its possible values (by which order?). One at a time, we try to assign a value to each cell and keep searching from the resulting position.
MyCell[,] backtrackingSearch(MyCell[,] branch)
{
MyCell[,] ret;
if (branch == null) return null;
if (isFinish(branch)) return branch;
Pos s = SelectUnassignedVariable(branch);
while (branch[s.ln, s.col].Value.Length > 0)
{
char c = SelectDomainValue(branch, s);
ret = backtrackingSearch(Assign(Clone(branch), s, c));
if (ret != null)
return ret;
m_NumOfBacktracking++;
branch = Eliminate(branch, s, c);
if (branch == null) return null;
}
Variable heuristics (Or: which cell should I try first?)
In the aforementioned search algorithm, I use the SelectUnassignedVariable function but it does not say anything about the criterion. That is because this 'function' is a delegate, for comparing some other heuristics. I write the backtracking search to be generic, I just change the delegate value from one to another.
So, what heuristics are there? A lot, and I hope someone who read this will come up with something I could explore and compare. I will talk about the classic ones, and the ones my program implements.
First unassigned value
This must be the simplest heuristic there is; it is very fast too, but on the other hand, a very stupid one. We just choose the first one we find, and it is used on brute force searches, but we want to be a little clever than that.
Pos FirstUnassignedCell(MyCell[,] branch)
{
for (int i = 0; i < m_gridSize; i++)
for (int j = 0; j < m_gridSize; j++)
if (!branch[i, j].assigned)
return new Pos(i, j);
return null;
}
Minimum Remaining Value (MRV) heuristic:
OK, finally a real heuristic. In this one, we will choose the cell with the minimum possibilities. The logic is that it is good because it has the most chance of guessing right. This also minimizes the branching factor .
Pos MinimumRemainingValues(MyCell[,] branch)
{
int min = m_gridSize + 1;
Pos p=new Pos() ;
for (int i = 0; i < m_gridSize; i++)
for (int j = 0; j < m_gridSize; j++)
{
if ((!branch[i, j].assigned) &&
(branch[i, j].Value.Length < min))
{
p.ln = i;
p.col = j;
min = branch[i, j].Value.Length;
}
}
return p;
}
MRV + Max Degree (MRV+MD)
OK, we have the MRV, and it sounds pretty good, but maybe, we can do it better. We still use MRV, but now as a tie breaker. We choose the cell with the maximum degree. The degree of a cell is the number of unassigned cells that are constrainted with the cell.
Pos MRV_With_MD(MyCell[,] branch)
{
return MaxDegree(branch, MinimumRemainingValuesList(branch));
}
List<Pos> MinimumRemainingValuesList(MyCell[,] branch)
{
int min = m_gridSize + 1;
List<Pos> list = new List<Pos>();
for (int i = 0; i < m_gridSize; i++)
for (int j = 0; j < m_gridSize; j++)
{
if ((!(branch[i, j].assigned)) && (branch[i, j].Value.Length == min))
{
list.Add(new Pos(i, j));
continue;
}
if ((!(branch[i, j].assigned))&& (branch[i, j].Value.Length < min))
{
list.Clear();
min = branch[i, j].Value.Length;
list.Add(new Pos(i, j));
}
}
return list;
}
Pos MaxDegree(MyCell [,]branch, List<Pos> MRVS)
{
int deg = -1;
Pos p =null;
for (int i = 0; i < MRVS.Count; i++)
{
int count = 0;
for (int k = 0; k < branch[MRVS[i].ln ,MRVS[i].col].Peers.Count; k++)
if (!branch[branch[MRVS[i].ln ,MRVS[i].col].Peers[k].ln,
branch[MRVS[i].ln ,MRVS[i].col].Peers[k].col].assigned)
count++;
if (count > deg)
{
deg = count;
p = MRVS[i];
}
}
return p;
}
This sounds better, but it will cost us computation time, so is it worth it? Not always. We will see some comparisons in the end.
Value heuristics
OK, we know how to choose our cell, now we need to choose which value from the possibilities (the domain) to try first, and this is called Value Heuristics.
Lexicographic Order heuristic:
As the start of the variable heuristics, here again, we start with the 'banal' one, we just choose the first.
char LexicographicOrderFirst(MyCell[,] branch, Pos variablePosition)
{
return branch[variablePosition.ln, variablePosition.col].Value[0];
}
Least Constraint Value heuristic:
In this heuristic, we choose the value which make the least trouble for the chosen cell peers; for example, if in our cell we have the possibilities 7 and 9, we check in how many of this cell's peers 7 appears in the domain, and we do the same for 9; the algorithm then chooses the number that least appears in the cell's peers' domain.
char LeastConstraintValue(MyCell[,] branch, Pos variablePosition)
{
int[] arr = new int[branch[variablePosition.ln, variablePosition.col].Value.Length];
for (int i = 0; i < arr.Length; i++)
arr[i] = 0;
for (int i = 0; i < branch[variablePosition.ln, variablePosition.col].Value.Length; i++)
for (int j = 0; j < branch[variablePosition.ln, variablePosition.col].Peers.Count; j++)
{
if (branch[branch[variablePosition.ln, variablePosition.col].Peers[j].ln,
branch[variablePosition.ln,
variablePosition.col].Peers[j].col].Value.Contains(
branch[variablePosition.ln, variablePosition.col].Value[i].ToString()))
arr[i]++;
}
return branch[variablePosition.ln, variablePosition.col].Value[GetMinIndex(arr)];
}
Points of interest
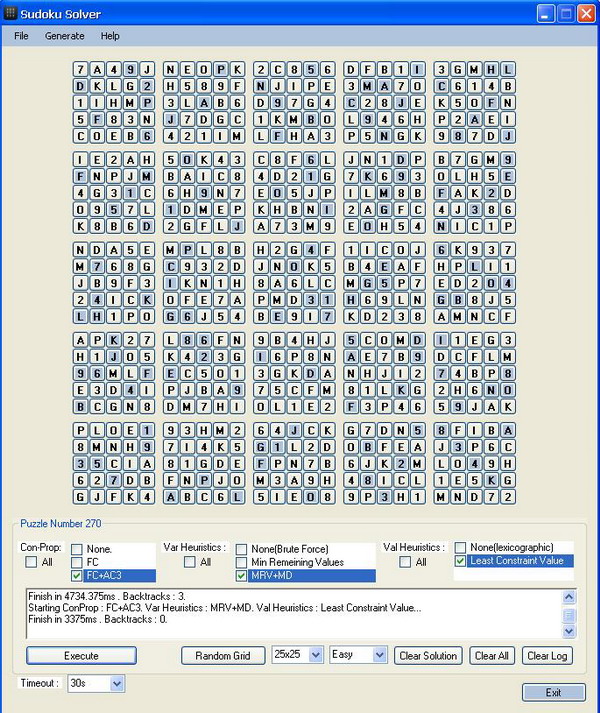
Heard all seen all! Let uss see how they work:

Improve my code!!!
The key reason for me to publish this article is to make a better and faster Sudoku solver, help me do that.
History
- First published on 25.3.09.
