Introduction
The cryptographic arms race between the good guys and the bad guys has led to the development of Authenticated Encryption schemes. Authenticated encryption offers confidentiality, integrity, and authenticity. This means our data is secure from both disclosure and tampering. CodeProject's Authenticated Encryption examined how easy it can be to tamper with data, and showed us how to use three dedicated block cipher modes of operation (EAX, CCM, and GCM) to ensure confidentiality and authenticity. The solution included the use of Crypto++, which many beginners have trouble with at times.
As an alternative to Crypto++ and to acclimate beginners to CAPI programming, we developed WinAES. The class only offered privacy - and not authenticity - so it would be relatively easy to covertly tamper with data under its protection. To strengthen WinAES so that we can actually use it in an application, we must add an authenticator for data authenticity assurances. To this end, we will add a HMAC to AES for a new class: WinAESwithHMAC.
WinAESwithHMAC will build upon WinAES. As with WinAES, the class will use only Windows CAPI in an effort to achieve maximum Windows interoperability. WinAESwithHMAC will use AES-CBC and HMAC-SHA1. We use SHA1 because it is available on XP and above, though we would prefer SHA-256 or a CMAC. A CMAC is essentially a CBC-MAC done right (refer to Authenticated Encryption and the use of a CBC-MAC on variable length messages).
WinAESwithHMAC is still aimed at the beginner. But this time around, we will also:
- wrap two Cryptographic Service Providers (CSP) in one object
- derive two keys from a master key or base secret
- use an HMAC during
CryptEncrypt and CryptDecrypt - use WinDbg to snoop rsaenh.dll to verify the correct order of operations
Encrypted Data Format
The output of an authenticated encryption scheme is the pair { cipher text, authenticator }. Cipher text is the customary encrypted data, and authenticator is the HMAC over the cipher text which provides authenticity assurances over the cipher text. Notationally, WinAESwithHMAC outputs C||a, where C = Enc(m), a = Auth(C). C||a is simply the { cipher text, authenticator } pair.
Because we want to allow a drop in replacement for objects which provide only encryption (such as WinAES), WinAESwithHMAC will append the authentication tag to the cipher text during encryption. Conversely, WinAESwithHMAC will remove the existing tag before decryption, and then use the existing tag to compare against the newly calculated HMAC (the HMAC is created during decryption over the cipher text). Details of why the authenticator is calculated over the cipher text - and not the plain text - can be found in Authenticated Encryption.
Intel Hardware Cryptographic Service Provider
The Intel Hardware Cryptographic Service Provider is available as a download in redistributable form. We will use it as the second provider in WinAESwithHMAC, but it is not needed for the correct operation of the class. By default, the flags passed through the constructor does not specify loading the Intel CSP. If INTEL_RNG is specified and the Intel CSP is not available, the class will fall back to the primary CSP for pseudo random bytes. Our code to load the providers is as follows:
static const PROVIDERS IntelRngProvider[] =
{
{ INTEL_DEF_PROV, PROV_INTEL_SEC, 0 }
};
...
for( int i = 0; (m_nFlags & INTEL_RNG) &&
(i < _countof(IntelRngProvider)); i++ )
{
if( CryptAcquireContext( &m_hRngProvider, NULL,
IntelRngProvider[i].params.lpwsz,
IntelRngProvider[i].params.dwType,
IntelRngProvider[i].params.dwFlags ) ) {
break;
}
}
if( NULL == m_hRngProvider ) {
assert( NULL != m_hAesProvider );
m_hRngProvider = DuplicateContext( );
}
When using the Intel generator, be aware that the generator is blocking. So, you might consider using the Intel generator to seed the AES Provider's generator.
Keying
The WinAES class uses one key, calling CryptImportKey to insert the provided key material into the Windows key store. WinAESwithHMAC requires two keys. One key is used for encryption, and one key is used for authentication. This means WinAESwithHMAC needs 32 bytes of key material for AES-128 - 16 bytes for encryption and 16 bytes for authentication. We can use one of two keying strategies in WinAESwithHMAC. First, we can require the caller to provide all 32 bytes when using AES-128 (and 64 bytes for AES-256) for keying needs. This seems a bit unreasonable to me, so we will use the second method.
The second method uses the provided 16 bytes (or 32 bytes for AES-256) as a base secret from which we derive the encryption and authentication keys. This seems most reasonable to me, since we know that the extra keying material is relatively safe to use because we control the derivation process. What we want to avoid (from the user) is the lack of key independence. If the authentication key is recovered by the attacker, the attacker should not be able to determine the encryption key (and vice-versa). If one key were simply derived from another, a compromise of the first key could reveal the second (derived) key. To mitigate this behavior, we will control the derivation process.
Pseudo Random Functions and Key Derivation Functions allow us to create additional key material from existing key material. NIST offers guidance on PRFs and KDFs through SP 800-108. Not surprisingly, Microsoft's implementation of key derivation is implemented in CryptDeriveKey. When we casually say that we "derive the keys", a lot is going on under the hood in CryptDeriveKey. But, before we use this function, we need to understand its behavior. First, the pseudo code for MSDN's Example C Program: Deriving a Session Key from a Password.
HASH hash = CryptCreateHash(...)
hash.Update( key material )
KEY key = CryptDeriveKey( hash )
As offered, the code is both simple and secure (the operative word is secure). The MSDN sample demonstrates that a low entropy source, such as a password, can be used to create a session key. So far, so good. Next, we modify the program as follows to accommodate the creation of a session key and a mac key, as shown below.
HASH hash = CryptCreateHash(...)
hash.Update( key material )
KEY session = CryptDeriveKey( hash )
KEY mac = CryptDeriveKey( hash )
When we examine the key material of session and mac, we find the keys are identical. For those who have familiarized themselves with Authenticated Encryption, using the same key to both encrypt the data and authenticate the data causes the cipher-text to be independent of the plaintext. The authentication mechanism is rendered completely insecure. And, to make matters worse, CryptDeriveKey does not indicate any type of failure when using the AES Provider. The evil derivation is shown in Figure 1.
|
Figure 1: Evil Key Derivation
|
So, we modify the program as follows to ensure a second hashing:
HASH hash = CryptCreateHash(...)
hash.Update( key material )
KEY session = CryptDeriveKey( hash )
HASH hash = CryptCreateHash(...)
hash.Update( session key )
KEY mac = CryptDeriveKey( hash )
The code above, though better than the first, suffers from the fact that keys are not independent - the mac key is derived directly from the session key. In the scheme above, the method used to derive the keys may aide in recovering the keys (in essence, we are showing the attacker the output of two stages of the keying operation). Figure 2 shows the operation.

|
Figure 2: Evil Key Derivation
|
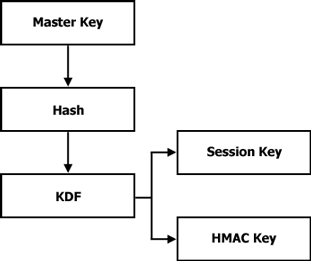
In an effort to achieve key independence, we need to use the provided key material as a 'master key' and combine it with additional information when deriving the keys. The pseudo code for what we desire is as follows. In the code, Km is the master key (a 'base secret') provided by the caller. We use Km to derive Ke and Ka - the encryption and authentication keys, respectively.
SetKey( key_m, keysize )
{
k_e = DeriveKey( Hash( key_m, encryption ) )
k_a = DeriveKey( Hash( key_m, authentication ) )
}
In the pseudo code above, we use the same base material with additional constant information before calling CryptDeriveKey. The method we use to employ uniqueness among keys is similar to RFC 2898's KDF1. This is shown in Figure 3.

|
Figure 3: Key Derivation
|
We should not use the output of the hash directly as the session or mac key, since CryptDeriveKey will serve as the PRF and KDF (see the discussion of key derivation for the CryptDeriveKey function). The class' DeriveKey function is as follows. The key is passed in from SetKey or SetKeyWithIV, and the label is the unique data for the key we desire.
DeriveKey(const byte* key, unsigned ksize, const byte* label,
unsigned lsize, HCRYPTKEY hKey)
{
if(!CryptCreateHash( hProvider, CALG_SHA1, 0, 0, &hHash)) {
}
if (!CryptHashData( hHash, key, ksize, 0) ) {
}
if (!CryptHashData( hHash, label, lsize, 0) ) {
}
if (!CryptDeriveKey( hProvider, CALG_AES_128, hHash, dwFlags, &hKey)) {
}
}
The code above hard codes SHA1 and AES-128, but the class code allows more flexibility. Also of interest is dwFlags. In the MSDN samples, keys are derived for use in a stream cipher such as RC2, so dwFlags is 0. In the case of a block cipher such as AES, we must pass in the desired key size in the upper WORD. So, for AES-128, dwFlags = 128 << 16, and for AES-256, dwFlags = 256 << 16. If we wanted to examine the derived keys for uniqueness, the lower WORD would include CRYPT_EXPORTABLE.
HMAC Generation
Before we examine the changes to the encryption and decryption routines, we first look at how we create an HMAC using CAPI. MSDN offers the sample Creating an HMAC, and it serves as the basis for our use. The pseudo code is as follows:
HMAC_INFO info
info.AlgId = CALG_SHA1
HCRYPTHASH hash = CryptCreateHash(..., CALG_HMAC, HMAC key, ...)
CryptSetHashParam(..., HP_HMAC_INFO, info, ...)
We see that an HMAC is constructed slightly different than a hash. Most notable is the HMAC key as a parameter to CryptCreateHash.
Plain Text and Cipher Text Sizes
WinAESwithHMAC will append the HMAC to the cipher text during encryption, and remove the tag during decryption. So, a call to MaxCipherTextSize now includes the addition of the HMAC, which is 20 bytes. Recall that SHA1 is 160 bits or 20 bytes. The opposite is true for MaxPlainTextSize in the preparation for the decryption - the size requirement is 20 bytes less than the size of the cipher text.
Encryption and Decryption
Two changes occur in the encryption and decryption functions. First is the use of an HMAC, whose creation is described above. Second is that we pass the HMAC handle to the encrypt (or decrypt) function so that CAPI can encrypt and hash at the same time.
Encryption
Our call to the encryption function is as follows. In the code below, WinAES would pass NULL to CryptEncrypt, while WinAESwithHMAC will pass a handle to a hash object.
HCRYPTHASH hash = NULL;
if( !CryptCreateHash(m_hAesProvider, CALG_HMAC, m_hHmacKey, 0, &hHash)) {
}
if( !CryptSetHashParam(hHash, HP_HMAC_INFO, (byte*)&info, 0)) {
}
DWORD dsize = psize;
if( !CryptEncrypt( m_hAesKey, hHash, TRUE, 0, buffer, &dsize, bsize )) {
}
On successful encryption, all that remains is to append the HMAC to the cipher text as follows. The HMAC calculated by CAPI during encryption is a tag over the cipher text. Details of why the authenticator is calculated over the cipher text - and not the plain text - can be found in Authenticated Encryption.
DWORD hsize = HMAC_TAGSIZE;
if (!CryptGetHashParam( hHash, HP_HASHVAL, &buffer[dsize], &hsize, 0)) {
}
dsize is the out parameter received from CryptEncrypt which indicates the size of the cipher text written to the buffer. &buffer[dsize] is passed to CryptGetHashParam since it is the first byte immediately following the cipher text.
Decryption
Decryption is very similar to encryption, except that we must adjust the size of the cipher text by that of the HMAC which is appended to the cipher text. Also note that the HMAC is calculated over the cipher text we feed to the decryption routine. When decryption is complete, we have to compare the existing HMAC with the calculated HMAC. So, our decryption function is as follows:
HCRYPTHASH hash = NULL;
if( !CryptCreateHash(m_hAesProvider, CALG_HMAC, m_hHmacKey, 0, &hHash)) {
}
if( !CryptSetHashParam(hHash, HP_HMAC_INFO, (byte*)&info, 0)) {
}
DWORD dsize = (DWORD)csize-HMAC_TAGSIZE;
if( !CryptDecrypt( m_hAesKey, hHash, TRUE, 0, buffer, &dsize, bsize )) {
}
Upon a successful decryption, we retrieve the calculated HMAC (over the presented cipher text) and compare it to the existing HMAC, as follows:
DWORD hsize = HMAC_TAGSIZE;
BYTE hash[ HMAC_TAGSIZE ];
if (!CryptGetHashParam( hHash, HP_HASHVAL, hash, &hsize, 0)) {
}
if( !(0 == memcmp( hash, &buffer[csize-hsize], hsize )) ) {
}
What is AES Provider's Order of Operations?
After reading Authenticated Encryption, we know that there are two generally accepted ways to combine encryption and authentication (part of the table from Authenticated Encryption is reproduced below). Under certain conditions, Authenticate-Then-Encrypt (AtE) is secure under some constructions (yellow), while Encrypt-Then-Authenticate (EtA) is always secure (green).
| Method | Operation | Result |
| AtE | a = Auth(m), C = Enc(m||a) | C |
| EtA | C = Enc(m), a = Auth(C) | C||a |
So, our question is, What order of operations does the AES Cryptographic Service Provider use? To answer the question, we must turn to WinDbg. We run Sample.exe under the WinDbg debugger. Once started, the debugger breaks immediately. We use this halt to set our first break point after examining loaded modules.

|
Figure 4: Initial WinDbg Breakpoint
|
The commands we enter are shown above in blue. lm lists the loaded modules (note that rsaenh.dll is not yet loaded). We then try to breakpoint on Sample!WinAESwithHMAC::Encrypt, which causes WinDbg to prompt us for more information. So, we issue bp 0044b2d0 (we want to break on the Encrpyt that uses a common buffer). We then press g to run the program. If all goes well, the next prompt we should see is that the breakpoint was encountered.
Breakpoint 0 hit
eax=0012f978 ebx=7ffd8000 ecx=0012fe38 edx=0012f990 esi=004c8119 edi=0012fded
eip=0044b2d0 esp=0012f868 ebp=0012fe80 iopl=0 nv up ei pl nz na po nc
cs=001b ss=0023 ds=0023 es=0023 fs=003b gs=0000 efl=00000202
Sample!WinAESwithHMAC::Encrypt:
0044b2d0 55 push ebp
Since we are getting ready to encrypt, the rsaenh module must be loaded (it is not loaded until Sample.exe calls the Windows CryptAcquireContext). So, we query for exported symbols in the module as shown in Figure 5. We already know that the function names of interest from rsaenh.dll begin with CP, so we enter xrsaenh!CP*.

|
Figure 5: RSA Enhanced Provider Exports of Interest
|
Since we want to know the order of operation, our next two breakpoints are rsaenh!CPEncrypt and rsaenh!CPHashData. We set the breakpoints and then observe the program execution as in Figure 6.

|
Figure 6: Order of Operation Observed in WinDbg
|
As we can see from the output of WinDbg, the AES Enhanced Provider is first performing Encryption, then performing Authentication. So, we know that Microsoft is using the provably secure Encrypt then Authenticate.
Sample Program
The sample program is available for download as Sample.zip and shown below. On the surface, there is no difference between the sample program in WinAES (which performs only encryption) other than to exercise the ability to encrypt and decrypt from a common buffer. However, it is now nearly impossible to tamper with the cipher text undetected.
WinAESwithHMAC aes;
byte key[ WinAESwithHMAC::KEYSIZE_256 ];
byte iv[ WinAESwithHMAC::BLOCKSIZE ];
aes.GenerateRandom( key, sizeof(key) );
aes.GenerateRandom( iv, sizeof(iv) );
char message[] = "Microsoft AES Cryptographic Service "
"Provider test using AES-CBC/HMAC-SHA1";
const int BUFFER_SIZE = 1024;
byte buffer[BUFFER_SIZE];
size_t psize = strlen(message)+1;
size_t csize=0, rsize=0;
memcpy_s(buffer, BUFFER_SIZE, message, psize);
aes.SetKeyWithIv( key, sizeof(key), iv, sizeof(iv) );
SecureZeroMemory( key, sizeof(key) );
if( !aes.Encrypt(buffer, BUFFER_SIZE, psize, csize) ) {
cerr << "Failed to encrypt plain text" << endl;
}
if( aes.Decrypt(buffer, BUFFER_SIZE, csize, rsize) ) {
cout << "Recovered plain text" << endl;
}
else {
cerr << "Failed to decrypt plain text" << endl;
}
